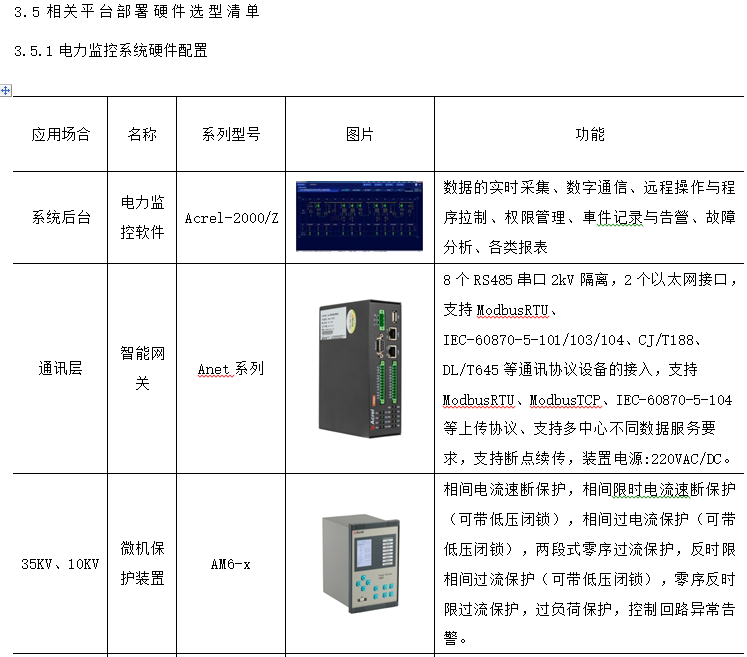
梯度下降求函数极小值

Himmelblau 函数表达式

$$\int (x,y)=(x^2+y-11{)}^2+(x+y^2-7{)}^2$$

Himmelblau.py 绘制

import numpy as np
import matplotlib.pyplot as plt

# from mpl_toolkits.mplot3d import Axes3D

def himmelblau(x):
    # himmelblau 函数实现，传入参数 x 为 2 个元素的 List
    return (x[0] ** 2 + x[1] - 11) ** 2 + (x[0] + x[1] ** 2 - 7) ** 2


x = np.arange(-6, 6, 0.1) # 可视化的 x 坐标范围为-6~6
y = np.arange(-6, 6, 0.1) # 可视化的 y 坐标范围为-6~6
print('x,y range:', x.shape, y.shape)

# 生成 x-y 平面采样网格点，方便可视化
X, Y = np.meshgrid(x, y)
print('X,Y maps:', X.shape, Y.shape)
Z = himmelblau([X, Y]) # 计算网格点上的函数值

# 绘制 himmelblau 函数曲面
fig = plt.figure('himmelblau')
# 设置 3D 坐标轴
ax = fig.add_subplot(1,2,1, projection = '3d')
ax.plot_surface(X, Y, Z, edgecolor='royalblue', lw=0.5, rstride=8, cstride=8,alpha=0.3) # 3D 曲面图

# 绘制等高线 x y z 平面
ax.contour(X, Y, Z, zdir='z', offset=-100, cmap='coolwarm',levels=60)
ax.contour(X, Y, Z, zdir='x', offset=-8, cmap='coolwarm')
ax.contour(X, Y, Z, zdir='y', offset=8, cmap='coolwarm')

ax.view_init(elev=20., azim=-35, roll=0)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')


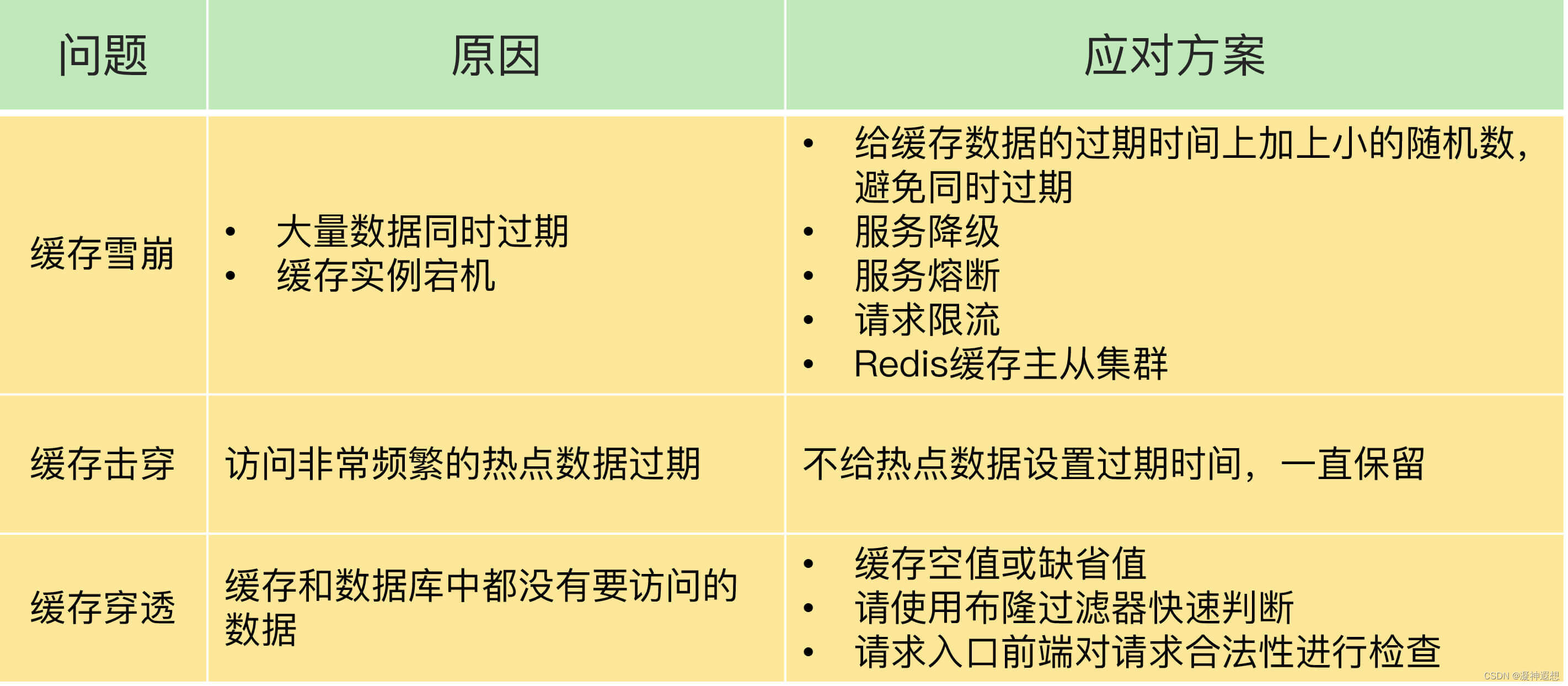
# 绘制等高线
ax = fig.add_subplot(1, 2, 2)
plt.xlim(-10, 10)
plt.ylim(-10, 10)
ax = plt.contour(X, Y, Z, levels=60 , cmap=plt.cm.cool) # 
# add label
plt.clabel(ax, inline=True)


plt.show()

利用 TensorFlow 自动求导 梯度下降求极小值

import tensorflow as tf
# 参数的初始化值对优化的影响不容忽视，可以通过尝试不同的初始化值，
# 检验函数优化的极小值情况
# [1., 0.], [-4, 0.], [4, 0.]
x = tf.constant([4., 0.]) # 初始化参数
for step in range(200):# 循环优化 200 次
    with tf.GradientTape() as tape: #梯度跟踪
        tape.watch([x]) # 加入梯度跟踪列表
        y = himmelblau(x) # 前向传播
    # 反向传播
    grads = tape.gradient(y, [x])[0]

    # 更新参数,0.01 为学习率
    x -= 0.01*grads
    # 打印优化的极小值
    if step % 20 == 19:
        print ('step {}: x = {}, f(x) = {}'.format(step, x.numpy(), y.numpy()))