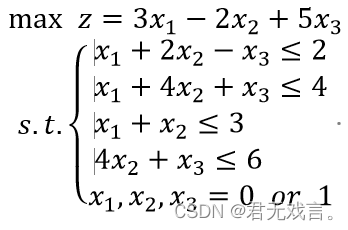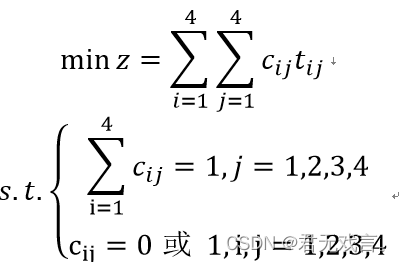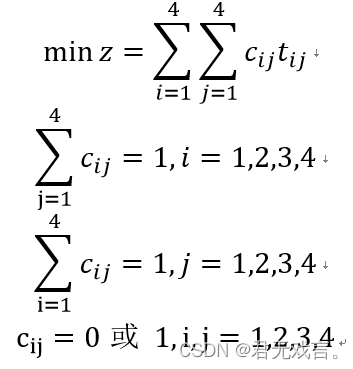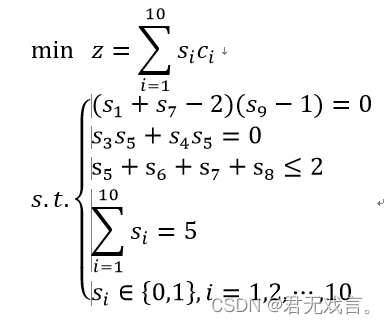| 一、实验目的: 1. 掌握分支定界法原理。整数规划求解的分枝定界法,首先确定目标函数的一个初始上下界,然后通过逐步分支使上界减小,下界增大,直到两者相等时,就求出了最优值和最优解。 2. 掌握用数学软件求解整数规划的方法; 3. 实验从算法思想、实验步骤与程序、运行结果、结果分析与讨论等几方面完成; 4. 预习整数规划的求解方法原理分枝定界法的基本思想。 | ||
| 二、实验内容
数学模型:
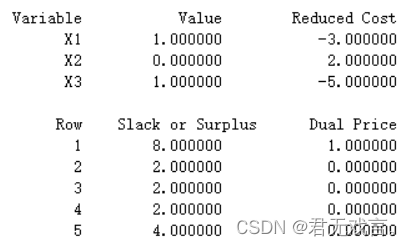
程序代码: MODEL: MAX=3*X1-2*X2+5*X3; X1+2*X2-X3<2; X1+4*X2+X3<4; X1+X2<3; 4*X2+X3<5; @BIN(X1); @BIN(X2); @BIN(X3); 程序执行结果:
结果解释: 该模型为PILP(纯整数线性规划)。当x1取1,x2取0,x3取1时,z取得最大值8. 变量x1对应的Reduced cost值为-3,表示当前非基变量x1的值增加一个单位时,目标函数减少-3,即最优目标函数值为8+3=11;变量x2对应的Reduced cost值为0,即x2为基变量;变量x3对应的Reduced cost值为-5,表示当前非基变量x1的值增加一个单位时,目标函数减少-5,即最优目标函数值为8+5=13;
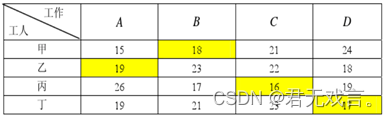
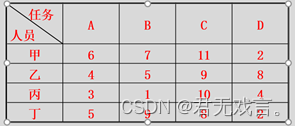
消耗的时间如下表:
问指派哪个人去完成哪项工作,可使总的消耗时间为最小? 数学模型:
程序代码: MODEL: sets: worker/1..4/; job/1..4/; link(worker,job):c,t; endsets data: t=15 18 21 24 19 23 22 18 26 17 16 19 19 21 23 17; enddata min=@sum(link:c*t); @for(job(j):@sum(worker(i):c(i,j))=1); @for(worker(i):@sum(job(j):c(i,j))=1); @for(link:@bin(c)); end 程序执行结果:
结果解释: 该模型为纯整数线性规划(PILP)。派遣甲完成工作2,乙完成工作1,丙完成工作3,丁完成工作4,可使总的消耗时间最短为70。变量c12对应的Reduced cost值为18,表示当前非基变量c12的值增加一个单位时,目标函数减少18,即最优目标函数值为70-18=52;变量c21对应的Reduced cost值为19,表示当前非基变量c21的值增加一个单位时,目标函数减少19,即最优目标函数值为70-19=51;变量c33对应的Reduced cost值为16,表示当前非基变量c33的值增加一个单位时,目标函数减少16,即最优目标函数值为70-16=54;变量c44对应的Reduced cost值为17,表示当前非基变量c44的值增加一个单位时,目标函数减少17,即最优目标函数值为70-17=53。
数学模型:
程序代码: model: sets: worker/1..4/; job/1..4/; link(worker,job):c,t; endsets data: t=6 7 11 2 4 5 9 8 3 1 10 4 5 9 8 2; enddata min=@sum(link:c*t); @for(job(j):@sum(worker(i):c(i,j))=1); @for(worker(i):@sum(job(j):c(i,j))=1); @for(link:@bin(c)); end 程序执行结果:
结果解释: 该模型为纯整数线性规划(PILP)。派遣甲将中文说明书译为俄语,乙将中文说明书译为英语,丙将中文说明书译为日语,丁将中文说明书译为德语,可使总的消耗时间最短为15。 变量c14对应的Reduced cost值为2,表示当前非基变量c14的值增加一个单位时,目标函数减少2,即最优目标函数值为15-2=13;变量c21对应的Reduced cost值为4,表示当前非基变量c21的值增加一个单位时,目标函数减少4,即最优目标函数值为15-4=11;变量c32对应的Reduced cost值为1,表示当前非基变量c32的值增加一个单位时,目标函数减少1,即最优目标函数值为15-1=14;变量c43对应的Reduced cost值为8,表示当前非基变量c43的值增加一个单位时,目标函数减少8,即最优目标函数值为15-8=7。
的钻探费用为最小。若10个井位的代号为s1,s2,…,s10,相应的钻探费用c1,c2,…,c10为5,8,10,6,9,5,7,6,10,8.并且井位选择上要满足下列限制条件: 试建立这个问题的整数规划模型,确定选择的井位。 数学模型: 取0-1变量s1,若si=1,则表示选取第i个井,若si=0,则表示不选取第i个井。建立数学模型如下:
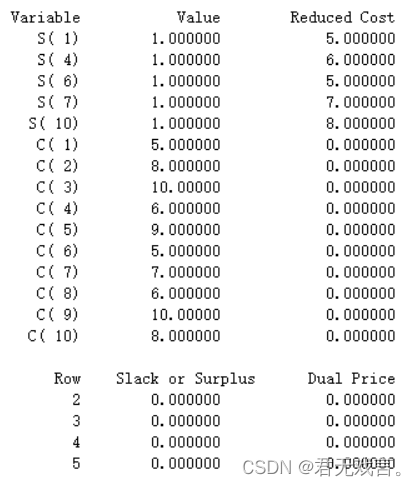
程序代码: MODEL: SETS: HANG/1..10/:S,C; ENDSETS DATA:C=5,8,10,6,9,5,7,6,10,8; ENDDATA MIN=@SUM(HANG(I):S(I)*C(I)); (S(1)+S(7)-2)*(S(9)-1)=0; S(3)*S(5)+S(4)*S(5)=0; S(5)+S(6)+S(7)+S(8)<=2; @SUM(HANG(I):S(I))=5; @FOR(HANG(I):@BIN(S)); END 结果解释:
根据程序运行结果: 该模型为PILP(纯整数线性规划)。确定钻井为s1,s4,s6,s7,s10。其费用分别为5,6,5,7,8,使总费用z最少为31 当前非基变量s1的值增加一个单位时,目标函数减少5,即最优目标函数值为33-5=28;非基变量s3的值增加一个单位时,目标函数减少10,即最优目标函数值为33-10=23;非基变量s4的值增加一个单位时,目标函数减少6,即最优目标函数值为33-6=27;当前非基变量s6的值增加一个单位时,目标函数减少5,即最优目标函数值为33-5=28;当前非基变量s7的值增加一个单位时,目标函数减少7,即最优目标函数值为33-7=26。 | ||
| 分析与讨论:
2.描述割平面法的过程。 在求解相应的线性规划时,首先要将原问题的数学模型进行标准化。这里的“标准化”有两个含义:第一是将所有的不等式约束全部转化成等式约束,这是因为要采用单纯形表进行计算的缘故。第二是将整数规划中所有非整数系数全部转换成整数,这是出于构造“切割不等式”的需要。其构造步骤如下: (1)先不考虑变量的取整约束,用单纯形法求解相应的线性规划问题,如果该问题没有可行解或最优解已是整数则停止,否则转下步。 (2)求一个“切割不等式”及添加到整数规划的约束条件中去,即对上述线性规划问题的可行域进行“切割”,然后返回步骤1。 |
最优化方法(基于lingo)之 整数规划问题求解(3/6)
news2026/2/8 12:00:12
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/690886.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
pdf可以转excel格式吗?分享两个快速转换方法给大家!
PDF文档常用于存储和共享信息,但在需要编辑或分析数据时,将PDF转换为Excel格式是一个常见需求。本文将向您介绍两种快速转换PDF为Excel格式的方法,让您轻松解决数据提取难题。无论您是处理大量数据还是需要转换复杂表格,这些方法都…
Ubuntu安装和配置ssh保姆教程
配置ssh常常遇到一些问题,接下来是避免踩坑,快速配置ssh 相信大家在设置ssh时,会碰到"Permission denied, please try again."
⚠️敲黑板:
有可能是密码输入错误 有可能是防火墙未关闭 有可能是连接机器的root用户没…
spring boot使用swagger简明笔记
1、什么是swagger
swagger就是一个在你写接口的时候自动帮你生成接口文档的东西,只要你遵循它的规范并写一些接口的说明注解即可。 本文springboot版本:2.5.6 2、引入依赖 <!-- swagger --><dependency><groupId>io.springfox</gr…
【论文阅读】Level-S2fM:神经隐式表面水平集上的SfM
【论文阅读】Level-S2fM:神经隐式表面水平集上的SfM Abstract1. Introduction2. Related Works2.1. Structure from Motion2.2. Neural Implicit Representation for 3D Scene 3. Preliminaries3.1. Neural Implicit Surface Rendering3.2. Ray Sampling and Sphere…
JavaScript—DomApi
DomApi 🔎Dom🔎Dom树🔎Dom—querySelector(获取元素)🔎事件事件的三要素 🔎操作元素获取 / 修改元素内容获取 / 修改元素属性获取 / 修改表单元素属性获取 / 修改样式属性修改内联样式修改元素应用的 CSS 类名 &#x…
Scrapy框架--settings配置 (详解)
目录 settings配置
官网-参考配置
配置文档 Scrapy默认BASE设置 settings配置 Scrapy框架中的配置文件(settings.py)是用来管理爬虫行为和功能的关键部分。它是一个Python模块,提供了各种配置选项,可以自定义和控制爬虫的行为。…
02【存储引擎、索引】
文章目录 一、存储引擎1.1 查看存储引擎1.2 修改默认存储引擎1.3 常见存储引擎1.4 存储引擎的特点1.4.1 InnoDB 存储引擎1.4.2 MyISAM 存储引擎1.4.2.1 MyISAM与InnoDB对比1.4.2.2 批量插入性能测试1.4.2.3 MyISAM压缩表 1.4.3 Merge 存储引擎1.4.4 Memory 存储引擎 二、索引2.…
kafka入门,发送原理和生产者重要参数(三)
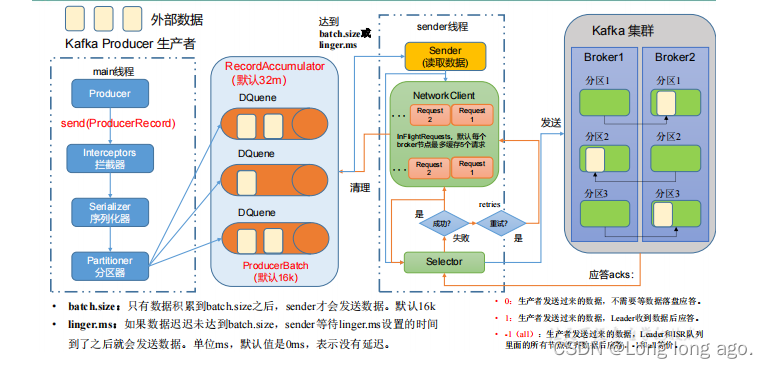
发送原理
在消息发送过程中,涉及两个线程,main线程和Sender线程。在main线程中创建了一个双端队列,RecordAccumulator,Sender过程不断从RecordAccumulator中拉取消息发送到Kafka Broker batch size:只有数据累计到batch.size之后࿰…
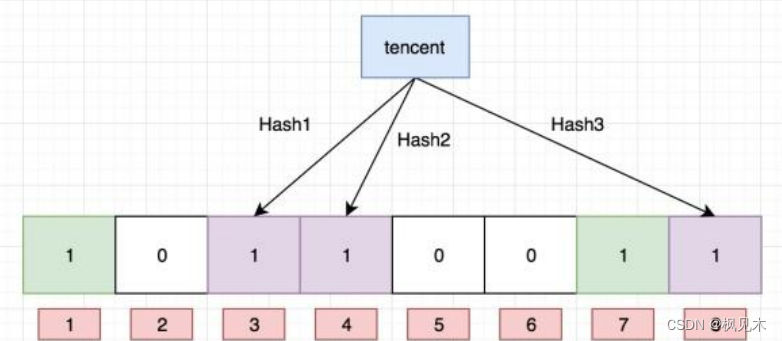
C++ 哈希思想应用 位图 布隆过滤器 海量数据处理
文章目录 问题引入位图(附C模拟实现源码)布隆过滤器(附C模拟实现源码) 问题引入
问题: 给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中。
问题…
连续6年霸榜全球工作站市场,Dell Precision凭什么?
前段时间,IDC发布2022 Q4工作站市场报告,戴尔拿下2022年工作站市场出货量和行业占比的双料冠军,且成为全年唯一一家份额增长的供应商。
至此,Dell Precision已连续6年蝉联世界第一。
根据IDC发布的2022年第四季度全球工作站追踪…
第四十章 开发Productions - ObjectScript Productions - 定义企业消息库
文章目录 第四十章 开发Productions - ObjectScript Productions - 定义企业消息库概述定义 Message Bank服务器添加Message Bank Helper类关于Message Bank的注意事项 第四十章 开发Productions - ObjectScript Productions - 定义企业消息库
概述
Enterprise Message Bank …
初识运营,明晰运营的学习路径
关于运营的思考
问题1:运营是什么?运营到底是做什么工作的?
如题:到底什么是运营?为什么我们所接触到的很多运营都不太一样,有的运营就是每天追寻互联网热点,加班加点的写文案;有的…
考研算法32天:桶排 【桶排序】
算法介绍
桶排
举个例子,一个数组中的数是:4 1 2 3 5,
然后桶排的顺序是:将每个数应该在的下标算出来,咋算呢?这我们就得考虑两种情况:假设我们设现在这个需要找到自己在数组里位置的数是x。…
自学黑客(网络安全),一般人我劝你还是算了吧(自学网络安全学习路线--第七章 数据库安全)【建议收藏】
文章目录 一、自学网络安全学习的误区和陷阱二、学习网络安全的一些前期准备三、自学网络安全学习路线一、数据库安全概述1、数据库的安全特性 二、数据库中的数据保护2、数据库加密3、数据库完整性保护 三、数据备份与恢复1、数据库备份2、数据库恢复 四、SQL Servre数据库安全…
vue写法——使用js高阶函数实现多条件搜索功能
🙂博主:爱学习的Akali king 🙂本文核心:vue写法——使用js高阶函数实现多条件搜索功能 目录 类比一下react写法用vue写法来实现,思路步骤:第一步:准备数据第二步:根据数据结构渲染Do…
ModaHub魔搭社区:向量数据库Milvus性能调优教程(一)
目录
性能调优
插入性能调优
查询性能调优
硬件环境
系统参数 性能调优
插入性能调优
“数据插入”到“数据写入磁盘”的基本流程请参考 存储操作。
如果数据量小于单次插入上限(256 MB),批量插入比单条插入要高效得多。
系统配置中…
Boom 3D For Win如何进行安装、激活和换机?
Boom系列应用软件又迎来了一位新的“猛将”— 隆重升级的Boom 3D(Windows系统)!这款主打3D环绕音效的软件,既能使用在Windows设备上,也能使用在MAC设备上。Boom 3D既可以让你体验到高质量的3D环绕音效,也能…
我们来谈谈websocket
"你一无所有地闯荡。" 一、初始WebSocket
(1) 什么是websocket WebSocket是一种在单个TCP连接上进行全双工通信的协议。 WebSocket使得客户端和服务器之间的数据交换变得更加简单,允许服务端主动向客户端推送数据。在WebSocket API中,浏览器和…
自学黑客(网络安全),一般人我劝你还是算了吧(自学网络安全学习路线--第九章 Internet安全协议)【建议收藏】
文章目录 一、自学网络安全学习的误区和陷阱二、学习网络安全的一些前期准备三、自学网络安全学习路线一、安全协议概述二、IPSec协议1、概述2、IP封装过程3、IPSec不安全性4、IPSec的功能5、IPSec体系结构6、IPSec的AH7、IPSec的AH8、IPSec的ESP9、IPSec的ESP10、ISAKMP11、IK…
分析油烟污染的危害及其控制防治对策 安科瑞 许敏
摘 要:介绍了烹饪油烟的组成及危害,着重概述了家庭烹饪油烟污染特点以及净化技术的研究进展,对各技术特点及存在的问题进行了分析,初步探讨了新近发展的静电催化耦合技术在烹饪排放污染控制中的应用,分析了现行的吸油烟…
推荐文章
- “让App玩捉迷藏:Android教育平板的‘隐身术’开发实录”
- AB Download Manager v1.5.8 开源免费下载工具
- git push origin masterremote: [session-bd46a49f] The token username invalid
- 豪越赋能消防安全管控,解锁一体化内管“安全密码”
- Redis(五)主从复制:主从模式介绍、配置、拓扑(一主一从结构、一主多从结构、树形主从结构)、原理(复制过程、数据同步psync)、总结
- PaddleHub 首页图像 - 文字识别chinese_ocr_db_crnn_server