0、引言

算法小计：本文阐述以下自己对于快速幂的理解，之前想了很久没想通。

        对于求一个数字a的n次方问题：，如果直接写循环，从1开始每次乘以a，求n次即可做出答案，但时间复杂度是O(n)，不太理想，由此引出快速幂的方法。

1、方法推导

        思考，试想任何一个十进制数都可以拆分为二进制的形式，例如10 -> (1010)2
        那么，7^10也就可以拆分为7^((1010)2)，再把 指数和形式 拆为 底数乘积 形式，显然为：

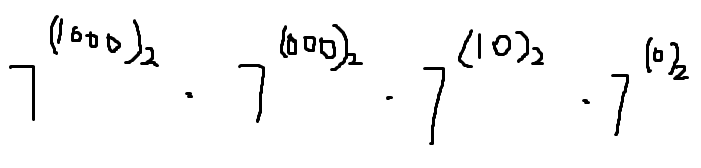
         我们发现，1010从低位到高位，分别对应着7^1、7^2、 7^4、 7^8...
         1.乘什么：如果每一轮的计算，都能够累积上一步的底数就好了!
        观察，发现每一轮的底数为上一轮的平方！意味着原来需要乘7、乘7、乘7....而现在是乘7、7^2、7^4.....因此每一轮都是原来速度的两倍，那么时间复杂度将变为log(n)

        2.要不要乘：通过将十进制拆分为二进制，依次判断每一位是否为1，如果是则乘以当前的底数，如果为0就不乘。

2、代码实现 

        二进制依次判断位数的实现，可以通过将a和 “1”求按位与&运算，如果得到1，说明末位为1
        每一轮结束右移一位，然后判断下一位。

然后在每一轮里：
        1.通过判断二进制位，来决定是否累乘到结果res上。
        2.让底数乘以自己来更新下一轮的底数。
        3.n右移一位

代码：

class Solution {
    public double myPow(double a, int n) {
        int res = 1
        while(n > 0) {//当n还存在位数
            if((n & 1) == 1) res *= a;    //1.判断、累乘
            a *= a;        //2.底数自乘更新
            n >>= 1;       //3.右移更新
        }
        return res;
    }
}

3.力扣：剑指 Offer 16. 数值的整数次方

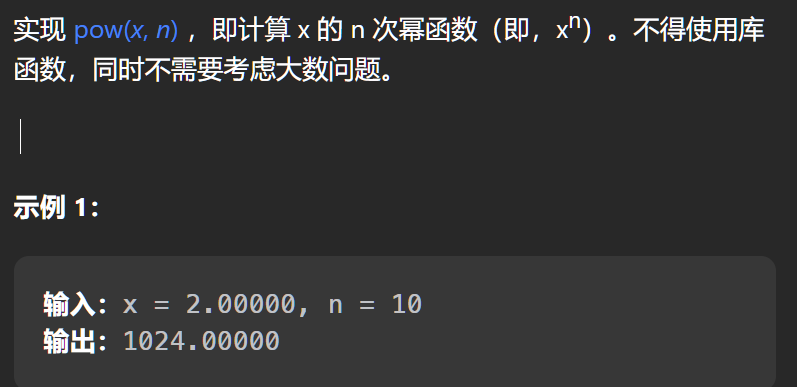
        原理相同，实现类似：

class Solution {
    public double myPow(double x, int n) {
        if(x == 0) return 0;
        long b = n;
        double res = 1.0;
        if(b < 0) {
            x = 1 / x;
            b = -b;
        }
        while(b > 0) {
            if((b & 1) == 1) res *= x;
            x *= x;
            b >>= 1;
        }
        return res;
    }
}