二叉树结构：
static class TreeNode{
public char val;
public TreeNode left;
public TreeNode right;
public TreeNode(char val) {
this.val = val;
}
@Override
public String toString() {
return this.val+"";
}
}一、前序遍历
前序遍历是一种访问二叉树的每一个结点的方法，它的遍历顺序是根节点，左子树，右子树。
1）递归版本
public void preOrder1(TreeNode root){
if(root==null){
return ;
}
System.out.println(root.val);
preOrder1(root.left);
preOrder1(root.right);
}递归版本其实很简单，就是按照它的遍历方式来写一下就可以，我们主要来介绍一下非递归的方法。
2）非递归版本
前序遍历的非递归方式就是将递归的版本的每一个过程都存储下来，而我们就需要一个辅助栈来帮助我们实现。
算法思想：
1.节点不为空，打印，入栈，遍历左子树
2.节点为空但是栈不为空，出栈顶元素，遍历栈顶元素右子树
3.节点为空栈也为空，结束程序
4.二叉树为空结束程序
按照上述的代码思路，我们可以实现代码如下：
public void preOrder2(TreeNode root){
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while(!stack.empty()||cur!=null){
if(cur!=null){
//打印根节点
System.out.print(cur.val+" ");
//根节点入栈
stack.push(cur);
//访问左子树
cur=cur.left;
}
else{
cur=stack.pop().right;
}
}
}运行结果：
二、中序遍历
中序遍历的顺序是左子树、根节点、右子树，所以递归的版本可以按照前序遍历的思路来实现。
1）递归版本
public void inOrder1(TreeNode root){
if(root==null){
return ;
}
inOrder1(root.left);
System.out.print(root.val+" ");
inOrder1(root.right);
}2）非递归版本
算法思想：
1.节点不为空，入栈，访问左子树
2.节点为空但是栈不为空，出栈顶元素，打印，访问栈顶元素的右子树
3.栈为空并且节点为空，结束遍历
4.二叉树为空结束遍历
下面是中序遍历的非递归形式的代码实现：
public void inOrder2(TreeNode root){
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while(!stack.empty()||cur!=null){
if(cur!=null){
stack.push(cur);
cur=cur.left;
}
else{
cur=stack.pop();
System.out.print(cur.val+" ");
cur=cur.right;
}
}
}运行结果：
三、后序遍历
后序遍历的顺序是左子树、右子树、根节点。
递归版本
public void postOrder1(TreeNode root){
if(root==null){
return ;
}
postOrder1(root.left);
postOrder1(root.right);
System.out.println(root.val);
}非递归版本
后序遍历和前两个的遍历方法会有写不同，我们拿中序遍历来说，中序遍历是在遍历完左子树的时候，出根节点，打印根节点，访问右子树，但是后序遍历我们在访问左子树的之后需要访问右子树，在访问根节点，所以我们根节点不能在访问左子树之后出栈，需要继续访问右子树，当我们右子树访问完之后再出栈，所有我们就是必须需要
算法思路：
1.遍历左子树并且将左子树入栈
2.左子树为空的时候，访问右子树，有两种可能右子树为空：打印根节点，标记根节点，防止重复打印；树不为空，继续访问右子树的左子树，重复上诉过程
public void postOrder2(TreeNode root){
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
TreeNode prev = null;
while(cur!=null||stack.empty()){
while(cur!=null){
stack.push(cur);
cur=cur.left;
}
TreeNode top = stack.peek();
if(top.right==null||top.right==prev){
System.out.print(top.val+" ");
prev=top;
stack.pop();
}
else{
cur=top.right;
}
}
}运行结果：
解释一下prev：
我们的二叉树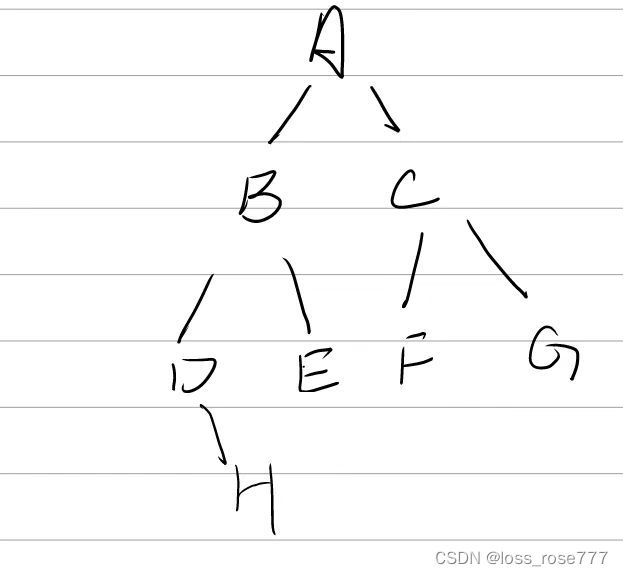
当我们左子树遍历到D的时候我们的栈有A、B、D此时右子树不为空继续遍历栈中加入H元素此时栈顶元素为H，其右子树为空我们打印H，删除栈顶元素H，按照程序继续走我们现在栈顶元素是D，D的右子树不为空继续将H加入栈中此时会出现死循环，所以我们需要用一个prev表示上一次打印元素，防止重复进入栈。
