本文为学校课程《机器学习》的期末复习材料，主要是关于一些机器学习模型的计算题的解答过程。

构造平衡 KD 树

给定一个二维空间的数据集: T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}，请构造一个平衡 KD 树。

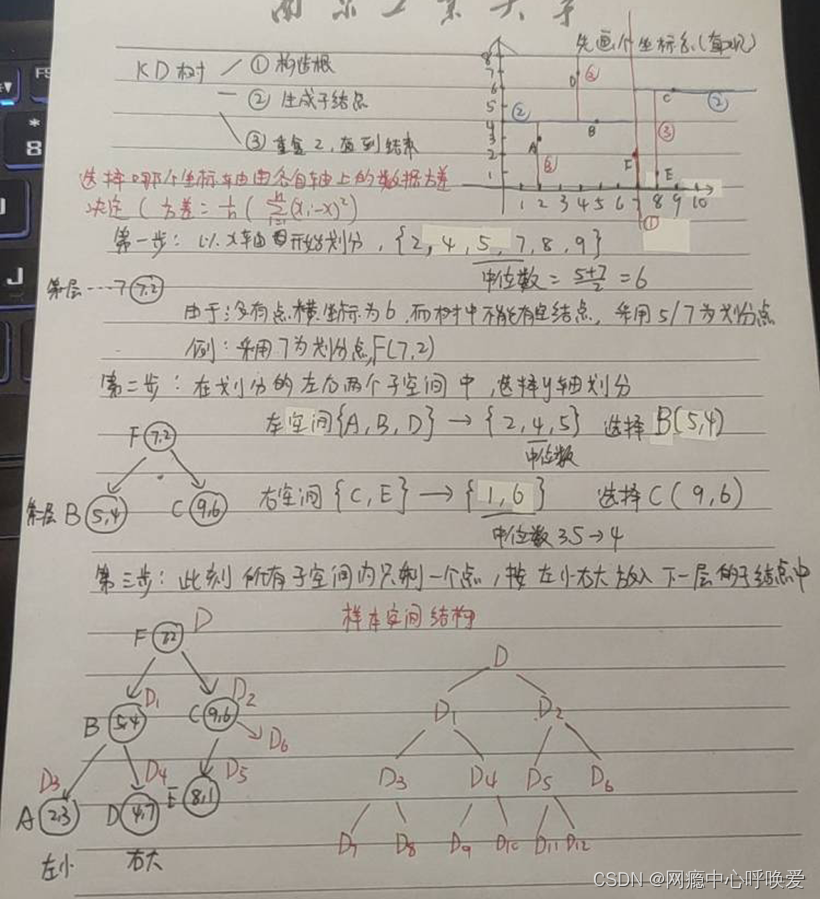
拓展：
k近邻-如何构造平衡kd树？
构建KD树

---

ID3 与 C4.5 算法构建决策树模型

利用 ID3 与 C4.5 算法构建决策树模型，要求写出计算过程并画出并决策树。



关于决策树的构建这方面的文章很多可以找一个看就行

---

朴素贝叶斯

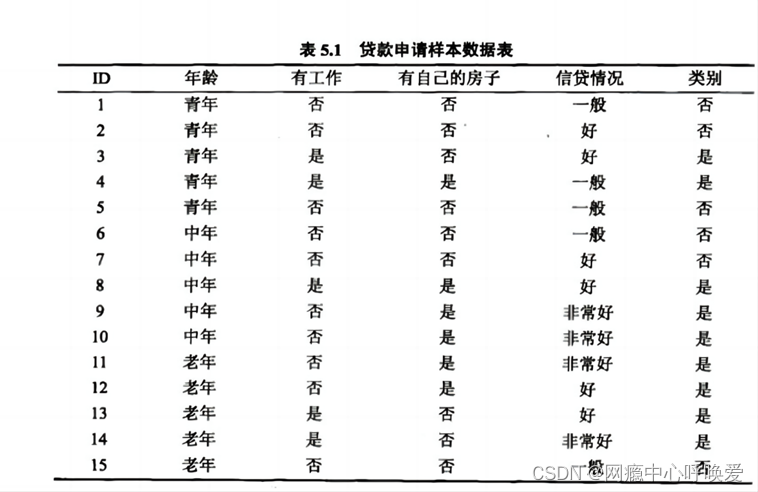
根据下表中的训练数据学习一个朴素贝叶斯分类器并确定x=(2,S)的类标记 y。表中X^((1))，X((2))为特征，取值的集合分别为 A={1, 2, 3}，A2{S, M, L}, Y 为类标记,Y={1,‐1}。

拓展
拓展1
拓展2

---

SVM求最大间隔分离超平面和分类决策函数

已知正样本 x1=(1,2), x2=(2,3), x3=(3,3)，负样本 x4=(2,1), x5 =(3,2)。试求最大间隔分离超平面和分类决策函数，并在图上画出分离超平面、间隔边界及支持向量。
建议看统计学习方法课本上面的SVM求解步骤

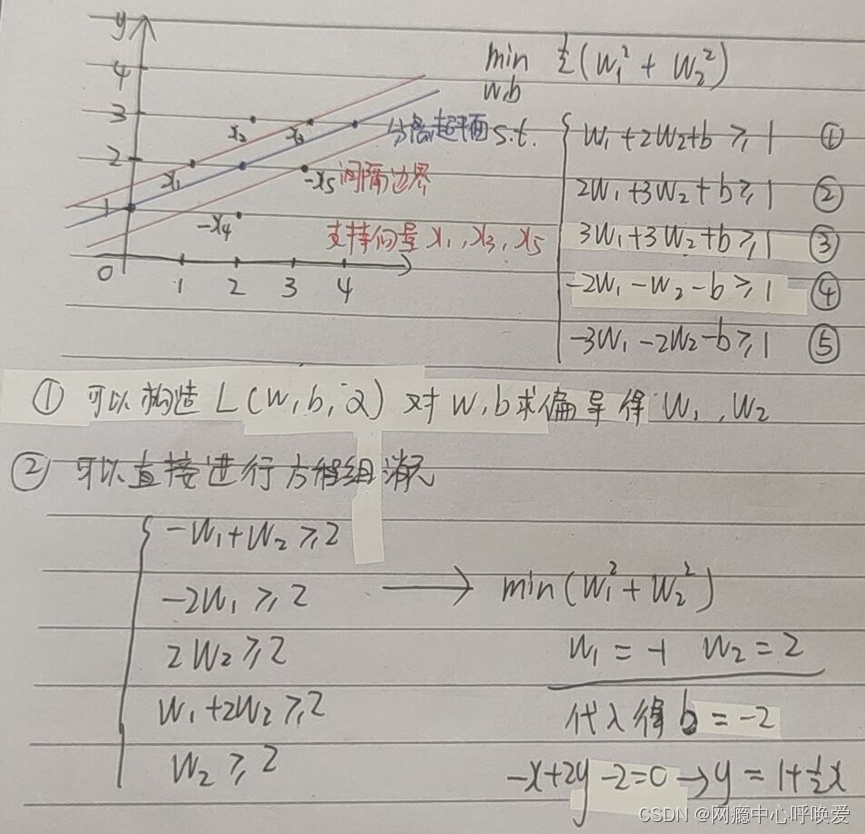
拓展
统计学习方法第七章答案
支持向量机（SVM）前戏-手动求解超平面方程
SVM求硬间隔最大超平面

---

EM算法

假设现在有两枚硬币 1 和硬币 2，随机抛掷后正面朝上概率分别为 P1，P2. 为了估计这两个概率，做实验，每轮取一枚硬币，连掷 5 下，共计掷五轮，记录下结果，如下表中所示。请应用 EM 算法估算出 P1 与 P2


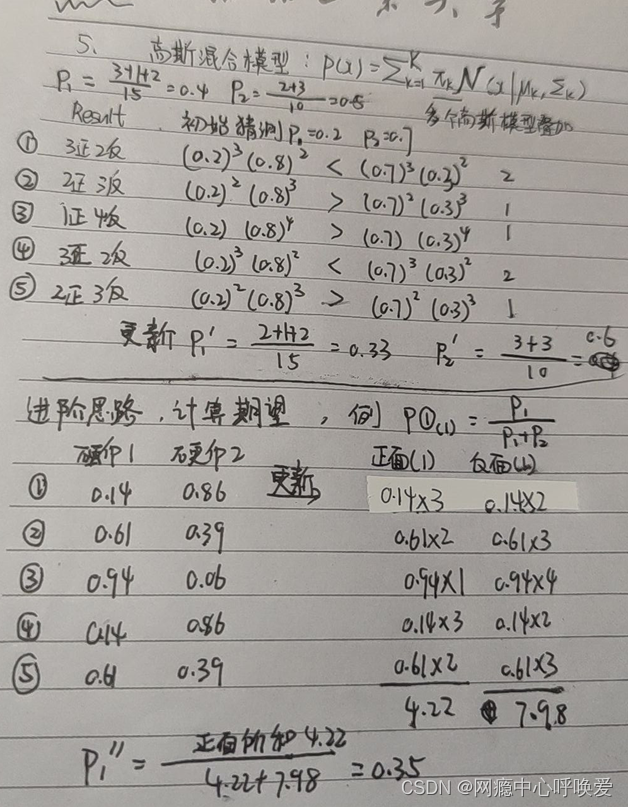
拓展
实例理解EM算法

---

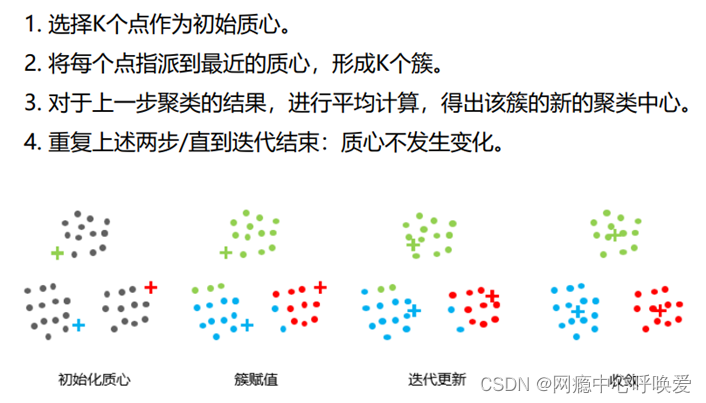
K-means聚类

假设数据集含有 9 个数据对象（用 2 维空间的点表示）：A1(3,1), A2(3,9), A3(8,6), B1(2,5), B2(2,4), B3(3,6), C1(2,6), C2(2,6), C3(2,2) 采用 k‐Means 方法进行聚类，距离函数采用曼哈顿距离，取k=3，假设三个簇的初始分别为 A1, B1,和 C1，求第一次循环结束时的三个簇的质心，要求写出计算过程。




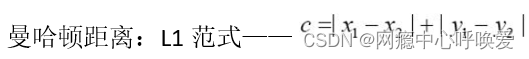
拓展
K-means聚类的实现以及案例讲解

---

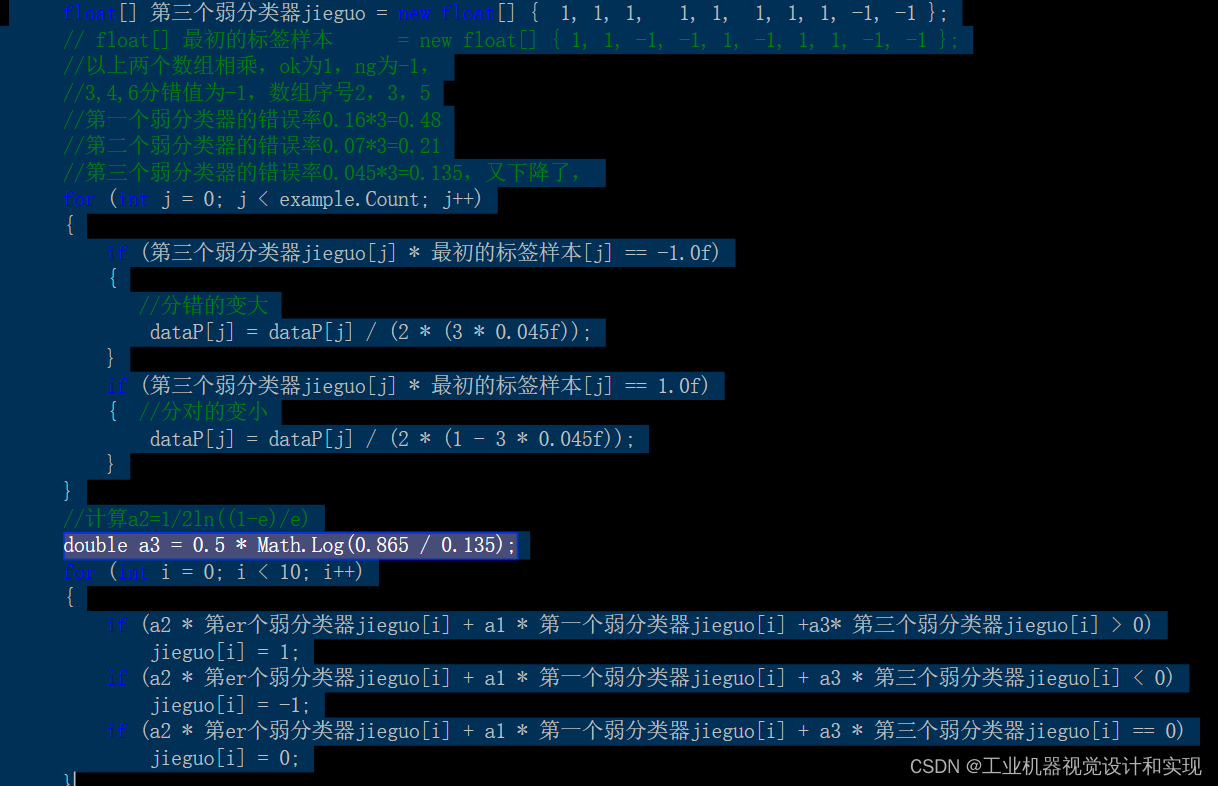
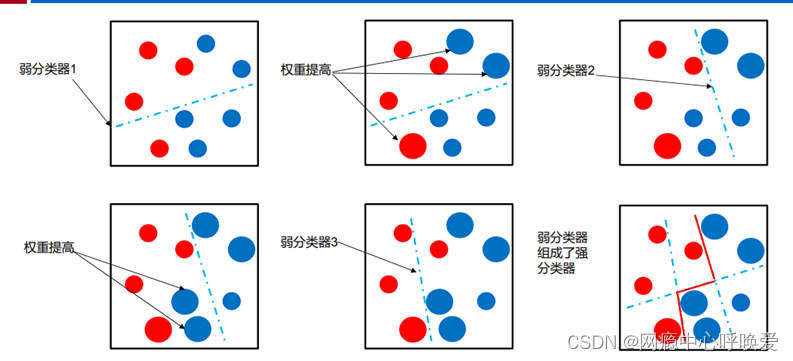
adaboost计算

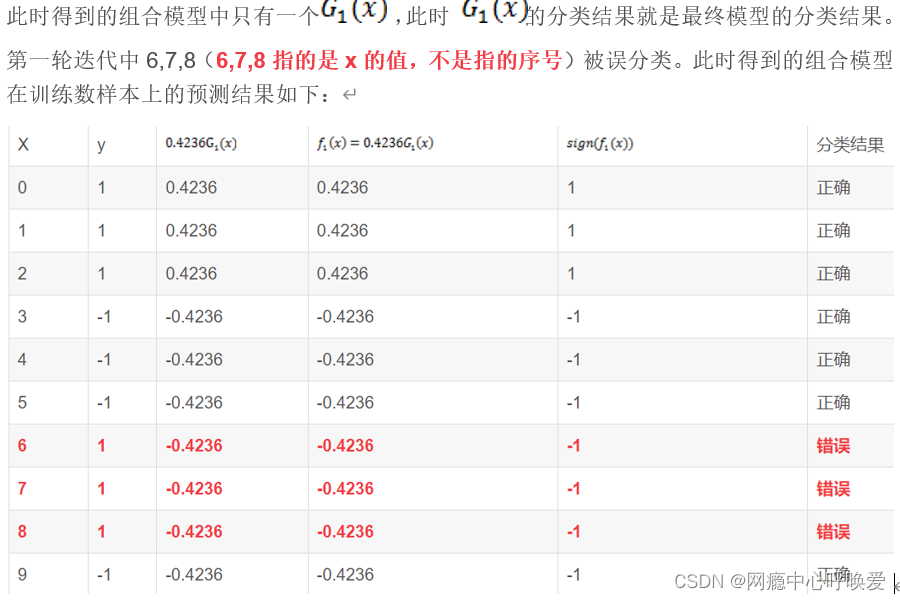
假设使用如下样本训练adaboost分类器，请计算第二轮迭代后样本的权重。

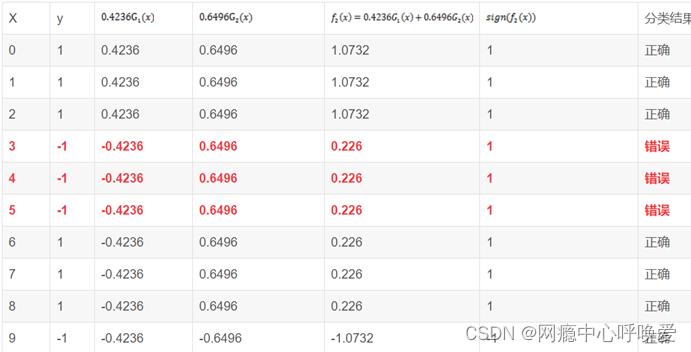
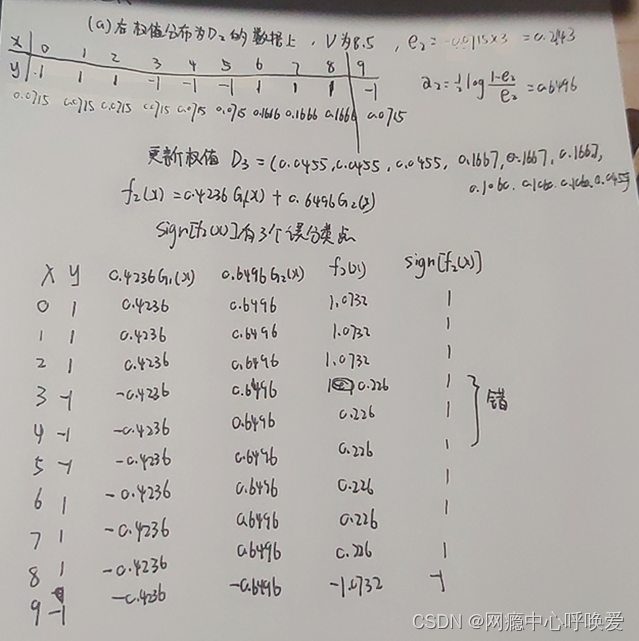
拓展
Adaboost 算法实例解析
AdaBoost例题

---

概率图模型

给定如下有向概率图模型，请写出p(x)的条件概率连乘形式

---

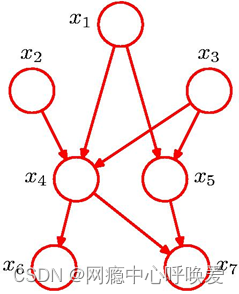
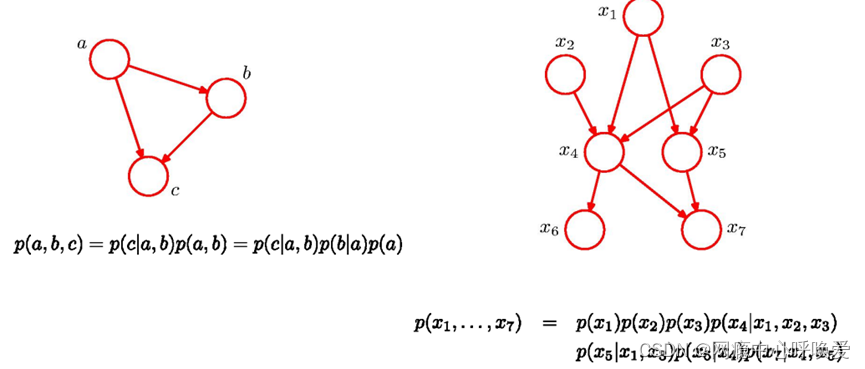
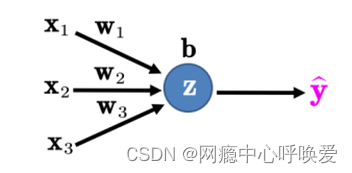
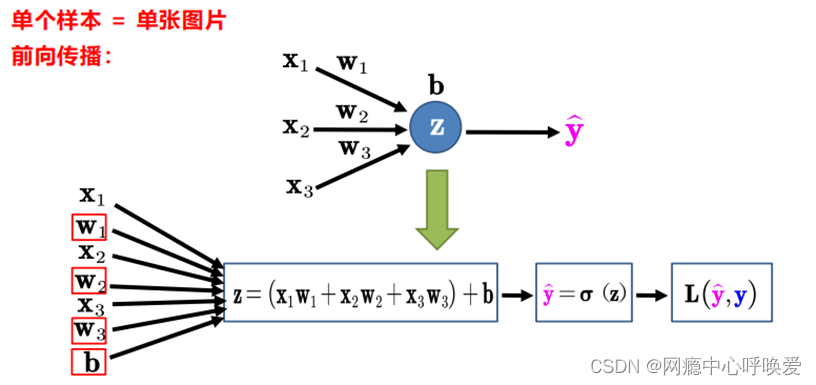
反向传播

以下图所示的单层神经网络为例，假设激活函数使用Sigmoid函数，损失函数采用交叉熵，请推导连接权重参数w与偏置b的偏导数。