1842A - Tenzing and Tsondu

题意

丁真和珍珠宝可梦对决, 每个宝可梦都有x战力, 假设有两个宝可梦, 其战力分别为a和b(a>b), 战力为a的宝可梦获胜后战力-b, 而战败的宝可梦会消失
最后还有宝可梦的人获胜
问你丁真和珍珠谁赢了

题解

显而易见, 赢下来的宝可梦可以继续打, 输了的就会消失, 所以是比战力值总和

代码

void solve()
{
    cin>>n>>m;
    vector<ll>a(n+1);
    ll u,v;
    u=v=0;
    rep(i,1,n) cin>>a[i],u+=a[i];
    vector<ll>b(m+1);
    rep(i,1,m) cin>>b[i],v+=b[i];
    if(u==v) cout<<"Draw"<<endl;
    else if(u>v)cout<<"Tsondu"<<endl;
    else cout<<"Tenzing"<<endl;
    return;
}

1842B - Tenzing and Books

题意

丁真收到了三堆书, 每堆书有$n$本, 每本书有固定的知识值$a[i]$
每读一本书就会使得丁真的知识值与这本书的知识值进行或运算
即$ans|=a[i]$
丁真会从书堆的开头第一本开始读
每当丁真不想读下去时, 他会直接放弃一整堆书
丁真想让他的知识值达到ans, 问你这可能吗

题解

因为是或运算, 思路直接来到了位运算
首先, 假设ans的二进制是10011
那么想要让丁真达到ans这个值, 我们需要注意一些点

因为是或运算, 书的知识值中二进制为0是不会对答案造成影响的
若同一个二进制位中, 书的知识值为1而答案为0, 那么就对答案造成了偏差
那么以贪心的思想, 只要不会对答案造成影响的(即$book>>i\&1$==1&&ans>>i&1!=0), 丁真都可以读

那么答案显而易见, 对所有能读的书都给读了, 遇到不能读的书就退出书堆, 最后对比答案就可以了

代码

void solve()
{
    cin>>n>>m;
    vector<ll> a(n+1);
    ans=0;  
    rep(i,1,n) cin>>a[i];
    rep(i,1,n)//这段for重复三遍
    {
        ll mk=0;
        for(ll j=0;j<=32;j++)
        {
            cnt=(m>>j)&1;
            ant=(a[i]>>j)&1;
            if((ant&&cnt==0)) 
            {
                mk=1;
                break;
            }
        }
        if(mk) break;
        ans|=a[i];
    }

    rep(i,1,n) cin>>a[i];
    rep(i,1,n)
    {
        ll mk=0;
        for(ll j=0;j<=32;j++)
        {
            cnt=(m>>j)&1;
            ant=(a[i]>>j)&1;
            if(ant&&cnt==0) 
            {
                mk=1;
                break;
            }
        }
        if(mk) break;
        ans|=a[i];
    }

    rep(i,1,n) cin>>a[i];
    rep(i,1,n)
    {
        ll mk=0;
        for(ll j=0;j<=32;j++)
        {
            cnt=(m>>j)&1;
            ant=(a[i]>>j)&1;
            if(ant&&cnt==0) 
            {
                mk=1;
                break;
            }
        }
        if(mk) break;
        ans|=a[i];
    }
    
    if(ans==m) yes
    else no

    return;
}

解法2

源代码出自
用&的方式省去了位运算枚举
很妙

1842C - Tenzing and Balls

题意

n个球排成一列, 每个球都有一个特定的颜色值
丁真可以选择两个颜色值一样的球, 删除这这两个球之间的所有球(包括这两个球)这个操作可以进行无限次
问你最多能删多少个球

题解

这题一开始以为是双指针假了, 其实是dp
使用两个数组进行动态规划
d数组用于存储这个元素的最优解, 而f数组用于存储当前下标的最优解(即答案)
则动态转移方程(设当前元素为x)

f[i]=min(f[i-1]+1,d[x]);//选择该元素的最优解(若没出现过则为INF), 或者不选(答案+1)
d[x]=min(f[i-1],d[x]);//该元素的最优解=当前局部最优解和元素最优解取min

最后答案为n-f[n]

代码

void solve()
{
    cin>>n;
    vector<ll>a(n+1),f(a),d(n+1,INF);
    rep(i,1,n)
        cin>>a[i];

    rep(i,1,n)
    {
        ll x=a[i];
        f[i]=min(f[i-1]+1,d[x]);
        d[x]=min(f[i-1],d[x]);
    }
    cout<<n-f[n]<<endl;
    return;
}

1842D - Tenzing and His Animal Friends

题意

这题题面很抽象, 我看了至少半小时才看懂(也可能是因为英语太菜了, 嗯造机翻)
最后看了公告才看懂的

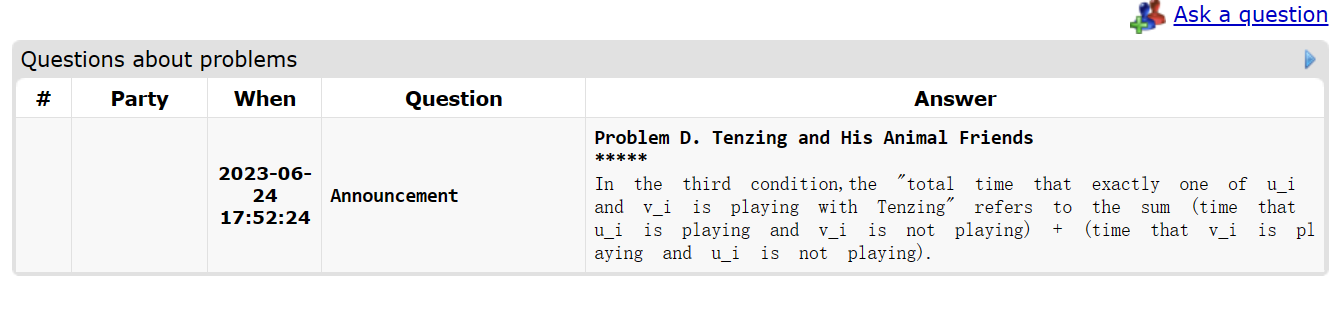
丁真和他的n个动物朋友玩耍, 丁真非常喜欢他的1号朋友, 所以每次都要和1号朋友玩, 丁真不喜欢他的n号朋友, 所以丁真不和n号朋友玩
现在给出m个限制, 每个限制有u v w三个参数, 代表u号朋友和v号朋友不在一起的时间不超过w
(u和v同时都在和同时不在的时间不会被此条限制所影响)
丁真想尽可能用更多的时间和动物朋友们玩耍
请输出丁真最多能和动物朋友玩耍的时间和玩耍的次数
用二进制状态表示丁真和哪些动物朋友们玩耍, 并在同一行那一次输出玩耍了多久

题解

首先1和n一定要在一个连通块中, 不一定需要1和n在一条边上但一定要在一个连通块中, 若1和n不在一个连通块中, 我们就可以一直构造11111…11110这样的玩法持续无限次, 因为1和n并不相连, 所以不存在只允许出1而不出现n的次数限制 (注意题目条件n不能出现, 1必须出现) , 因此可以一直构造这样的玩法
相应的, 从1到n的最短路, 也就是此题中丁真最多能和动物朋友有玩的时间了
(这题的难度就在这里了, 当时想破了脑袋也没想出这题是个最短路)
然后将数据分为两类, 一类是可以和1一起玩的, 另一类是不能和1一起玩的
按照贪心的思想, 每次都将能和1一起有玩的所有动物朋友都加进去, 而游玩时间就是其中能和1玩的动物朋友中, 能玩时间的最小值 (也就是他到n的最短路/或者1到n的最短路 这里取最小值 再减去上一个次游玩的时间, 原因是有上一次游玩时间和这一次游玩时间有交集部分 而交集部分正好是上一次游玩的时间)
按照这样下去, 每次游玩都必定淘汰至少一个

代码

void solve()
{
    cin>>n>>m;
    rep(i,1,n) 
        rep(j,1,n)
        {
            if(i!=j) cnt=llINF;
            else cnt=0;
            a[i][j]=cnt;
        }
        
    rep(i,1,m)
    {
        ll u,v,w;
        cin>>u>>v>>w;
        a[u][v]=a[v][u]=w;
    }

    rep(k,1,n)
        rep(i,1,n)
            rep(j,1,n)
            a[i][j]=min(a[i][j],a[i][k]+a[k][j]);
    if(a[1][n]==llINF)
    {
        cout<<"inf"<<endl;
        return;
    }

    vector<ll>d(n+1),dist;

    cnt=a[1][n];
    rep(i,1,n) 
    {
        d[i]=min(cnt,a[i][n]);
        dist.push_back(d[i]);
    }

    sort(dist.begin(),dist.end());
    dist.erase(unique(dist.begin(),dist.end()),dist.end());
    cout<<cnt<<' '<<dist.size()-1<<endl;
    cnt=0;
    repr(i,0,dist.size())
    {
        if(!dist[i]) continue;
        rep(j,1,n) cout<<(d[j]>=dist[i]);
        cout<<' '<<dist[i]-cnt<<endl;
        cnt=dist[i];
    }

    
    return;
}

这里用的Floyd求最短路, 当然你用dijkstra也是可以的