leetcode原题链接：旋转图像

题目描述

    给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

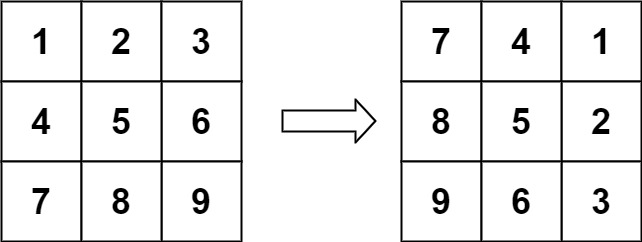
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

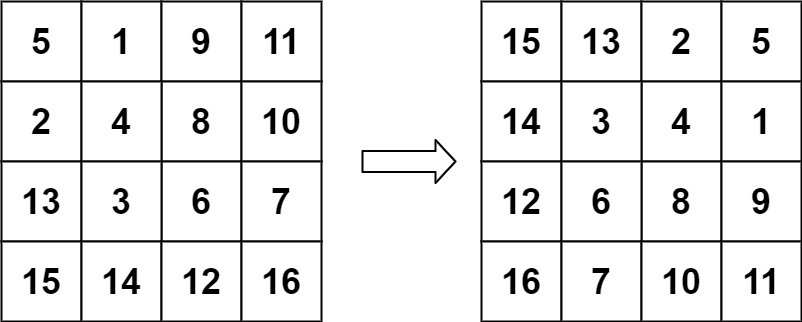
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]  

解题方法： 先上下对称翻转，再主对角线翻转。

可以观察旋转前后相同数字前后位置变化，找到翻转规律： 

先上下翻转： a[i][j] => a[n - 1 - i][j]

再主对角线翻转（即ij位置互换）: a[n - 1 - i][j]=> a[j][n - 1 - i]

所以，a[i][j]翻转后的位置变为a[j][n - 1 - i]

a[0][0] ==> a[0][2].     a[0][1] ==> a[1][2].      a[0][2] ==> a[2][2]

a[1][0] ==> a[0][1].    a[1][1] ==> a[1][1].      a[1][2] ==> a[2][1]

a[2][0] ==> a[0][0].     a[2][1] ==> a[1][0].     a[2][2] ==> a[2][0] 

C++代码

#include <iostream>
#include <vector>
#include <algorithm>
class Solution {
public:
    void rotate(std::vector<std::vector<int>>& matrix) {
        int n = matrix.size(); //n行
        int m = matrix[0].size(); //m列
        // 先上下翻转（通过交换元素的方式）
        for (int i = 0; i < n / 2; i++) {
            for (int j = 0; j < m; j++) {
                std::swap(matrix[i][j], matrix[n - 1 -i][j]);
            }
        }
        // 再沿着主对角线翻转(x,y)==>(y,x)
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < i; j++) { // i = j，落在主对角线上，但是主对角线上的元素不需要交换
                std::swap(matrix[i][j], matrix[j][i]);
            }
        }
    }
};