前言

介绍了常微分方程组的基本形式，并且介绍了matlab的数值和解析解法，以及给出了相应的案例。

1. 常微分方程组介绍

1.1 一阶常微分方程组

一阶常微分方程组为

$${\dot{x}}_i=f_i(t,\mathbf{x}),i=1,2,\cdots ,n$$

其中$\mathbf{x}$是状态表变量$x_i$组成的向量：$\mathbf{x}=[x_1,x_2,\cdots ,x_n{]}^T$，这称为系统的状态向量，$n$是系统的阶次，$f_i(\cdot )$是任意的非线性函数，$t$是时间变量。

1.2 高阶常微分方程组

matlab提供的微分方程数值解函数只能处理一阶微分方程组形式给出的方程，对于高阶常微分方程组我们需要变换为一阶微分方程组，微分方程组中我们需要选择一组状态变量，状态变量选择是任意的，所以这种变换不是唯一的，这里介绍微分方程组变换的一般方法。

1.2.1 形式1：单个高阶微分方程

单个高阶微分方程组写成：

$$y^{(n)}(t)=f(t,y(t),\dot{y}(t),\ddot{y}(t),\cdots ,y^{(n-1)}(t))$$

这里一个简单的状态变量的选择方法是令$x_1(t)=y(t),x_2(t)=\dot{y}(t),\cdots ,x_n(t)=y^{(n-1)}(t)$，于是我们有

$$\{\begin{array}{rl}{\dot{x}}_i(t)& =x_{i+1}(t),i=1,2,\cdots ,n-1\\ {\dot{x}}_n(t)& =f(t,y(t),\dot{y}(t),\ddot{y}(t),\cdots ,y^{(n-1)}(t))\end{array}$$

1.2.2 形式2：多个高阶微分方程组

对于高阶微分方程组：
$$\{\begin{array}{rl}{x}^{(m)}(t)& =f(t,y(t),\dot{y}(t),\ddot{y}(t),\cdots ,y^{(n-1)}(t))\\ y^{(n)}(t)& =g(t,y(t),\dot{y}(t),\ddot{y}(t),\cdots ,y^{(n-1)}(t))\end{array}$$

我们选择状态变量$x_1(t)=x(t),x_2(t)=\dot{x}(t),\cdots ,x_m(t)=x^{(m-1)}(t),x_{m+1}(t)=y(t),x_{m+2}(t)=\dot{y}(t),\cdots ,x_{m+n}(t)=y^{n-1}(t)$，可以做下面的转化：

$$\{\begin{array}{rl}{\dot{x}}_i(t)& =x_{i+1}(t),i=1,2,\cdots ,m-1\\ {\dot{x}}_m(t)& =f(t,x_1(t),x_2(t),\cdots ,x_{n+m}(t))\\ {\dot{x}}_i(t)& =x_{i+1}(t),i=m+1,m+2,\cdots ,m+n-1\\ {\dot{y}}_{n+m}(t)& =g(t,x_1(t),x_2(t),\cdots ,x_{n+m}(t))\end{array}$$

1.3 常微分方程组求解方法

1.3.1 数值解法

一般的常微分方程组很难找到解析解，这时候数值解就派上用场了。求解常微分方程式有很多方法，如Euler法，Runge-Kutta方法，Adams线性多步法，Gear法，刚性问题有若干求解方法，而隐式求解和含代数约束的微分代数方程则需要进行相应的变换。

matlab给出了若干求解一阶常微分方程组的函数，如ode23()（二阶三阶Runge-Kutta算法）、ode45()（四阶五阶Runge-Kutta算法）、ode15()（变阶次刚性方程求解算法），其调用格式一致如下：

[t,x]=ode45(方程函数名,tspan,x0,选项，附加参数)

其中

t是仿真结果的自变量组成的向量，一般是变步长算法。
x是一个矩阵，阶数是n，是微分方程的阶次，行数是t的行数，每一行对应相应时间处状态变量向量的转置。
方程函数名是matlab编写的固定格式的m函数，描述一阶微分方程组。
tspan是数值解的初始和终止的时间信息。
x0是初始状态变量。
选项是求解微分方程组的一些控制参数。
附加参数在求解函数和方程描述函数之间传递。

1.3.2 解析求法

常系数线性微分方程存在解析解，而变系数的线性微分方程可解性取决特征方程的可解性，一般是不可解析求解的，而非线性的微分方程式不存在解析解得，我们可以用matlab的dsolve()函数求解线性常系数微分方程的解析解，首先要先用syms命令声明符号变量，然后用dsolve函数求解。

2. 常微分方程组数值求解类型及案例

2.1 一阶微分方程组形式求解实例

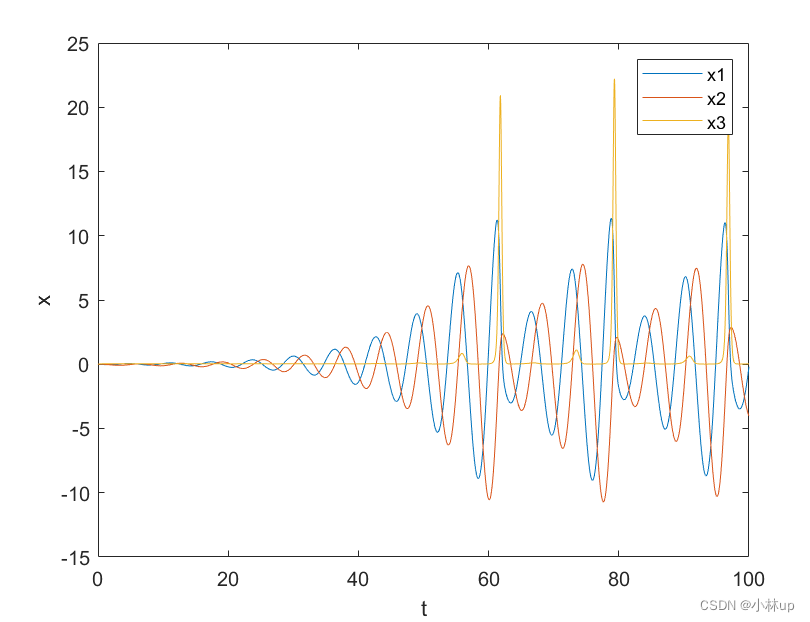
著名的Rossler化学反应方程组为：

$$\{\begin{array}{rl}{\dot{x}}_1(t)& =-x_2(t)-x_3(t)\\ {\dot{x}}_2(t)& =x_1(t)+a{x}_2(t)\\ {\dot{x}}_3(t)& =b+[x_1(t)-c]x_3(t)\end{array}$$

其中$a=b=0.2,c=5.7$，初值条件为$x_1(0)=x_2(0)=x_3(0)=0$.

2.1.1 编程方法1：微分方程组单独函数+主函数

1. 上式已经是标准型。不需要再化。
2. 定义微分方程组func

function dx = func(t,x) %不显含时间但是还是加上
a=0.2;
b=0.2;
c=5.7;
dx=[-x(2)-x(3);x(1)+a*x(2);b+(x(1)-c)*x(3)];
end

3. 主函数main

x0=[0;0;0];
[t,y]=ode45(@func,[0,100],x0);
plot(t,y);

结果：

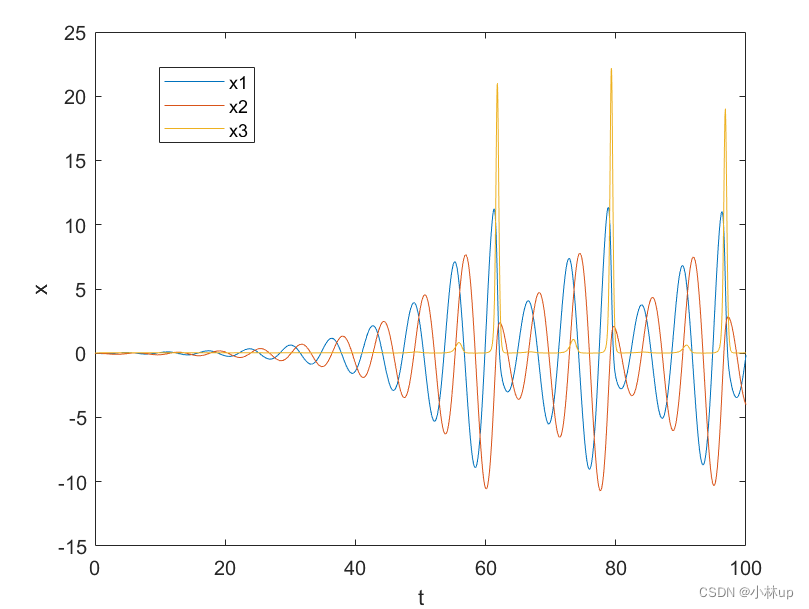
2.1.2 编程方法2：主函数（微分方程组匿名函数）

也可以写成匿名函数的形式，所有代码写在一个main函数里，也是一样的结果：

a=0.2;
b=0.2;
c=5.7;
f=@(t,x)[-x(2)-x(3);x(1)+a*x(2);b+(x(1)-c)*x(3)];
x0=[0;0;0];
[t,y]=ode45(f,[0,100],x0);
figure;
h=gcf;
set(h,'Color',	'#FFFFFF')
plot(t,y);
legend({'x1','x2','x3'});
xlabel('t');
ylabel('x');

2.1.3 option设置精度

matlab使用的是变步长算法，使用相对误差检验控制实际步长的选取，实际求解可以用opt=odeset设置，而相对误差检测量可以用RelTol指定，matlab默认的RelTol是$10^{-3}$，千分之一的误差，实际中我们可以设置更小的误差限看看是否结果一致，如果一致说明可以接受，否则就采取更小的误差限，我们接下来进行设置，在求解1的基础上我们修改main函数：

x0=[0;0;0];
opt=odeset;
opt.RelTol=1e-6;
[t,y]=ode45(@func,[0,100],x0,opt);
plot(t,y);

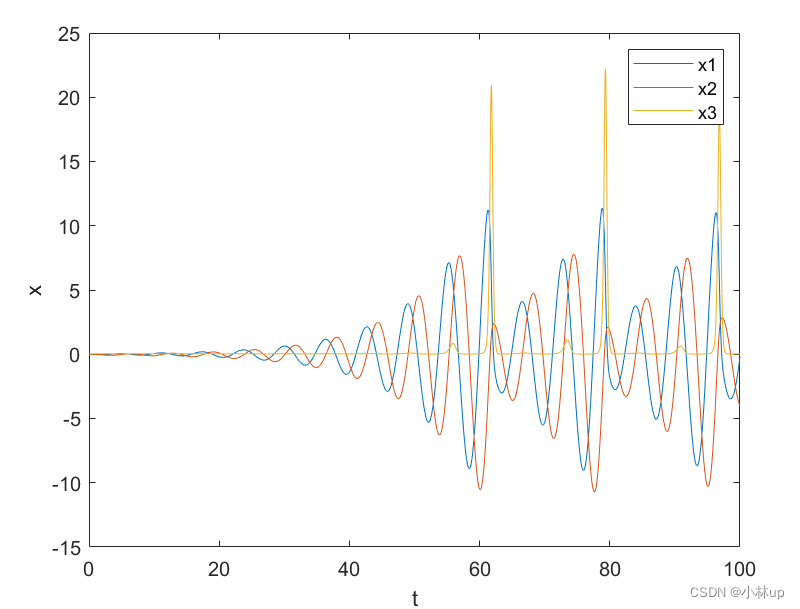
2.1.4 微分方程组参数由外部提供

我们如果想让$a,b,c$这三个参数在外部给出，可以写一个新的func函数：

function dx = func(t,x,a,b,c) %不显含时间但是还是加上
dx=[-x(2)-x(3);x(1)+a*x(2);b+(x(1)-c)*x(3)];
end

然后就是写外部的main函数给出三个参数$a,b,c$。

x0=[0;0;0];
opt=odeset;
opt.RelTol=1e-6;
a=0.2;
b=0.2;
c=5.7;
[t,y]=ode45(@func,[0,100],x0,opt,a,b,c);
figure;
h=gcf;
set(h,'Color',	'#FFFFFF')
plot(t,y);
legend({'x1','x2','x3'});
xlabel('t');
ylabel('x');

2.2 高阶微分方程组形式求解实例

2.2.1 单个高阶微分方程

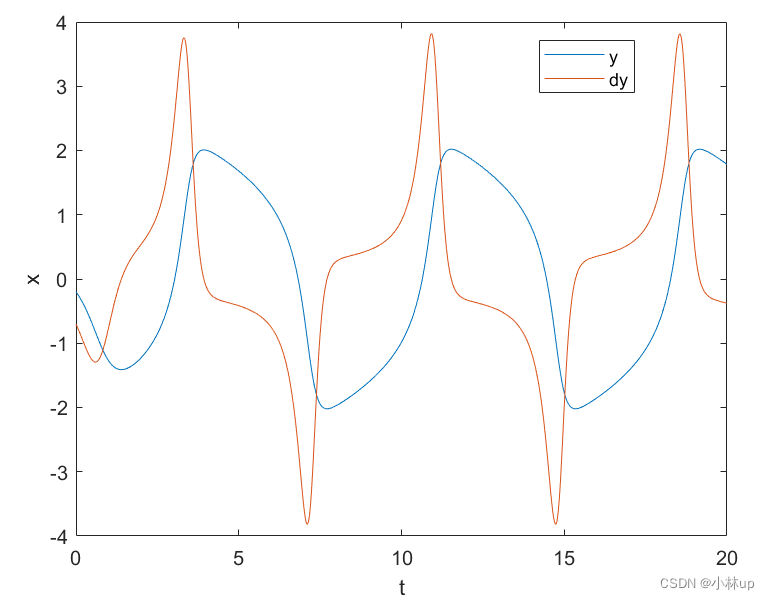
van der Pol方程
$$\ddot{y}(t)+2(y^2(t)-1)\dot{y}(t)+y(t)=0$$
初始条件为$y(0)=-0.2,\dot{y}(0)=-0.7$

按照前面所述选择$x_1(t)=y(t),x_2(t)=\dot{y}(t)$，转换为下面的形式：
$$\{\begin{array}{rl}{\dot{x}}_1(t)& =x_2(t)\\ {\dot{x}}_2(t)& =-2(x_1^2-1)x_2-x_1\end{array}$$

简单编写程序（这里采用匿名函数的写法）：

main

f=@(t,x)[x(2);-2*(x(1)^2-1)*x(2)-x(1)];
x0=[-0.2;-0.7];
opt=odeset;
opt.RelTol=1e-6;
[t,y]=ode45(f,[0,20],x0,opt);
figure;
h=gcf;
set(h,'Color','#FFFFFF')
plot(t,y);
legend({'y','dy'});
xlabel('t');
ylabel('x');

2.2.2 多个高阶微分方程组

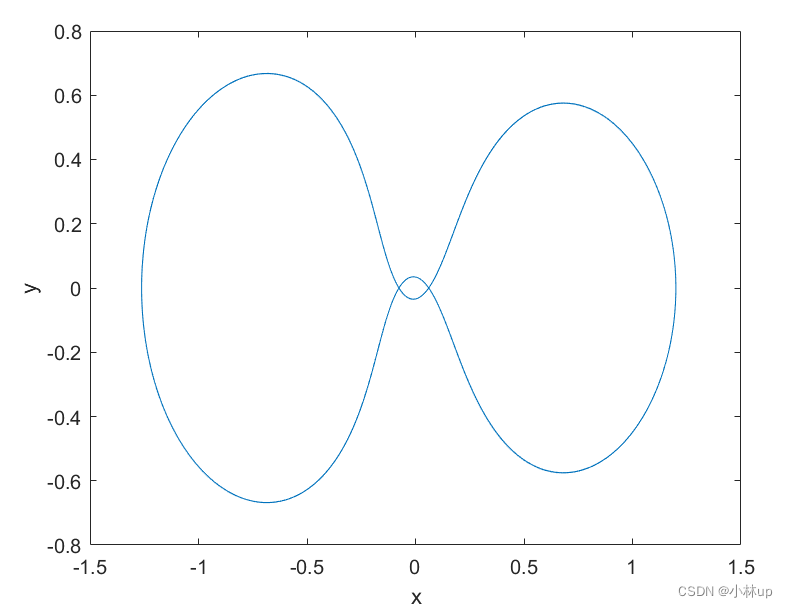
Apollo卫星运动轨迹$(x,y)$满足方程组：
$$\{\begin{array}{rl}\ddot{x}(t)& =2\dot{y}(t)+x(t)-{\mu }^{\ast }(x(t)+\mu )/r_1^3(t)-\mu (x(t)-{\mu }^{\ast })/r_2^3(t)\\ \ddot{y}(t)& =-2\dot{x}(t)+y(t)-{\mu }^{\ast }y(t)/r_1^3(t)-\mu y(t)/r_2(t{)}^3\end{array}$$
其中$\mu =1/82.45,{\mu }^{\ast }=1-\mu$,
$$r_1(t)=\sqrt{(x(t)+\mu {)}^2+y^2(t)},r_2(t)=\sqrt{(x(t)-{\mu }^{\ast }{)}^2+y^2(t)}$$
初始条件为：
$x(0)=1.2,\dot{x}(0)=0,y(0)=0,\dot{y}(0)=-1.04935751$

按照前面所述选择$x_1(t)=x(t),x_2(t)=\dot{x}(t),x_3(t)=y(t),x_4(t)=\dot{y}(t)$，转换为下面的形式：
$$\{\begin{array}{rl}{\dot{x}}_1(t)& =x_2(t)\\ {\dot{x}}_2(t)& =2x_4(t)+x_1(t)-{\mu }^{\ast }(x_1(t)+\mu )/r_1^3(t)-\mu (x_1(t)-{\mu }^{\ast })/r_2^3(t)\\ {\dot{x}}_3(t)& =x_4(t)\\ {\dot{x}}_4(t)& =-2x_2(t)+x_3(t)-{\mu }^{\ast }{x}_3(t)/r_1^3(t)-\mu x_3(t)/r_2(t{)}^3\end{array}$$
其中：
$$r_1(t)=\sqrt{(x_1(t)+\mu {)}^2+x_3^2(t)},r_2(t)=\sqrt{(x_1(t)-{\mu }^{\ast }{)}^2+x_3^2(t)}$$

微分方程组比较复杂，我们这里使用单独的函数func来写微分方程组：

func

function dx = func(t,x)
mu=1/82.45;mu1=1-mu;
r1=sqrt((x(1)+mu)^2+x(3)^2);
r2=sqrt((x(1)-mu1)^2+x(3)^2);
dx=[x(2);...
    2*x(4)+x(1)-mu1*(x(1)+mu)/r1^3-mu*(x(1)-mu1)/r2^3;...
    x(4);...
    -2*x(2)+x(3)-mu1*x(3)/r1^3-mu*x(3)/r2^3];
end

另外修改main函数为

main

x0=[1.2;0;0;-1.04935751];
opt=odeset;
opt.RelTol=1e-6;
[t,y]=ode45(@func,[0,100],x0,opt);
figure;
h=gcf;
set(h,'Color',	'#FFFFFF')
plot(y(:,1),y(:,3));
xlabel('x');
ylabel('y');

3. 常微分方程组解析求解案例

3.1 常系数线性微分方程求通解实例

$$\frac{{\mathrm{d}}^{4}y(t)}{\mathrm{d}{t}^4}+10\frac{{\mathrm{d}}^{3}y(t)}{\mathrm{d}{t}^3}+35\frac{{\mathrm{d}}^{2}y(t)}{\mathrm{d}{t}^2}+50\frac{\mathrm{d}y(t)}{\mathrm{d}t}+24y(t)={\mathrm{e}}^{-6t}\cos 5t+7{\mathrm{e}}^{-8t}+9$$

如果不给定初值，我们求的是一个通解，编写matlab代码如下

syms t y(t)
Y=dsolve(diff(y,4)+10*diff(y,3)+35*diff(y,2)+50*diff(y)+24*y==cos(5*t)*exp(-6*t)+7*exp(-8*t)+9);
pretty(simplify(Y))

3.2 常系数线性微分方程求特解实例

$$\frac{{\mathrm{d}}^{4}y(t)}{\mathrm{d}{t}^4}+10\frac{{\mathrm{d}}^{3}y(t)}{\mathrm{d}{t}^3}+35\frac{{\mathrm{d}}^{2}y(t)}{\mathrm{d}{t}^2}+50\frac{\mathrm{d}y(t)}{\mathrm{d}t}+24y(t)={\mathrm{e}}^{-6t}\cos 5t+7{\mathrm{e}}^{-8t}+9$$ 初始条件为$y(0)=5,\dot{y}(0)=0,\ddot{y}(0)=0,y^{(3)}(0)=0$

如果给定初值我们可以确定唯一解，我们加上初始条件，编写matlab代码如下

syms t y(t)
y1=diff(y);
y2=diff(y1);
y3=diff(y2);
Y=dsolve(diff(y,4)+10*y3+35*y2+50*y1+24*y==cos(5*t)*exp(-6*t)+7*exp(-8*t)+9,y(0)==5,y1(0)==0,y2(0)==0,y3(0)==0);
pretty(simplify(Y))

参考

1. 薛定宇《控制系统仿真与计算机辅助设计》P48-P51