某项目做了18次测试，每次测试发现的缺陷个数如下表所示：

测试序号	发现缺陷数
1	60
2	96
3	157
4	191
5	155
6	106
7	64
8	335
9	92
10	196
11	109
12	133
13	166
14	129
15	16
16	30
17	19
18	5

对上述的数据在ZenDAS中进行Gompertz曲线的拟合结果如下：

Gompertz模型

方法

曲线拟合算法：Levenberg-MarquardtGompertz

统计量描述

变量	N	累计值	轮次
发现缺陷数	18	2059	-
序号	18	-	18

求解Kab

Kab	估计值
K	2319.0866
a	0.0202
b	0.8092

快速上升的拐点识别

描述	值
缺陷快速上升的拐点t值	6.4323
缺陷快速上升的拐点y值	853.1443
当前测试的次数	18

缺陷目标值计算

描述	值
期望遗留缺陷率	5%
已发现的累计缺陷值	2059
应遗留的缺陷数	115.9543

实现目标的理想测试次数

描述	值
应发现的缺陷数	2203.1322
距离目标缺陷数差距	144.1322
还需测试的次数	3.4623

缺陷分析趋势图

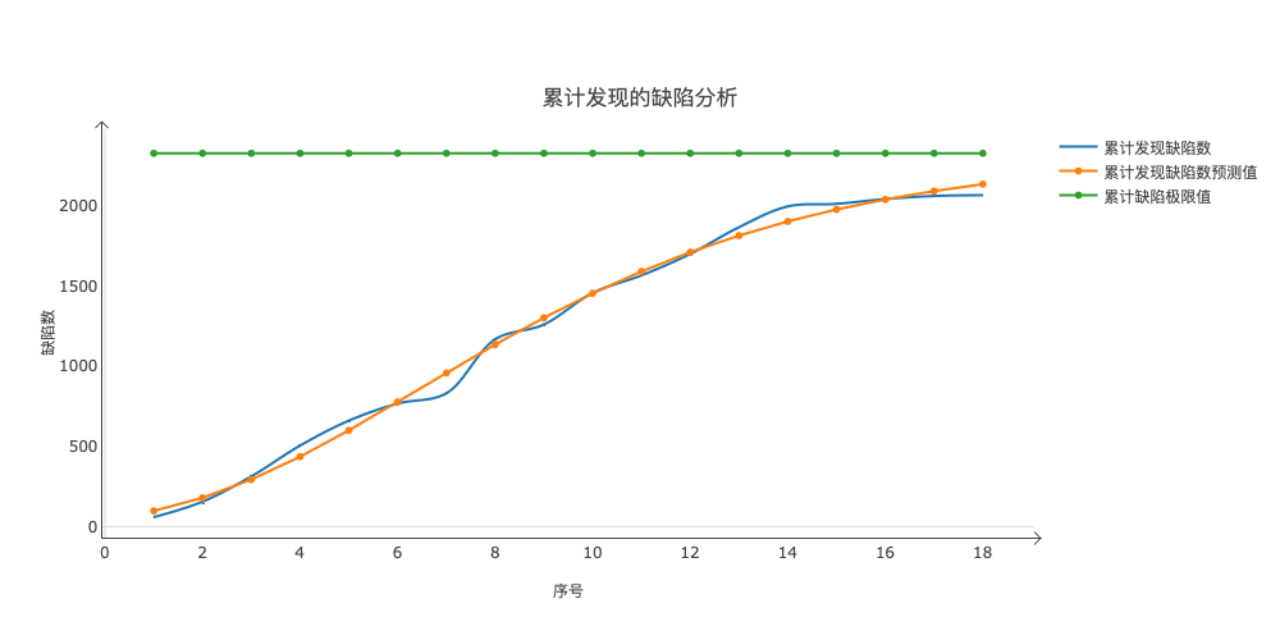
通过上述的分析可以发现：

1 软件中隐藏的缺陷数为：2319个。

2 如果设置缺陷遗留率为5%,则应该发现2203个缺陷。

3 当前已经发现了2059个缺陷，还需要再发现144个发现。

4 如果要再发现144个缺陷，还需要3-4次测试。

Gompertz模型的原理可以参考历史的这篇博客：

使用Gompertz模型预测非典的趋势_麦哲思科技任甲林的博客-CSDN博客