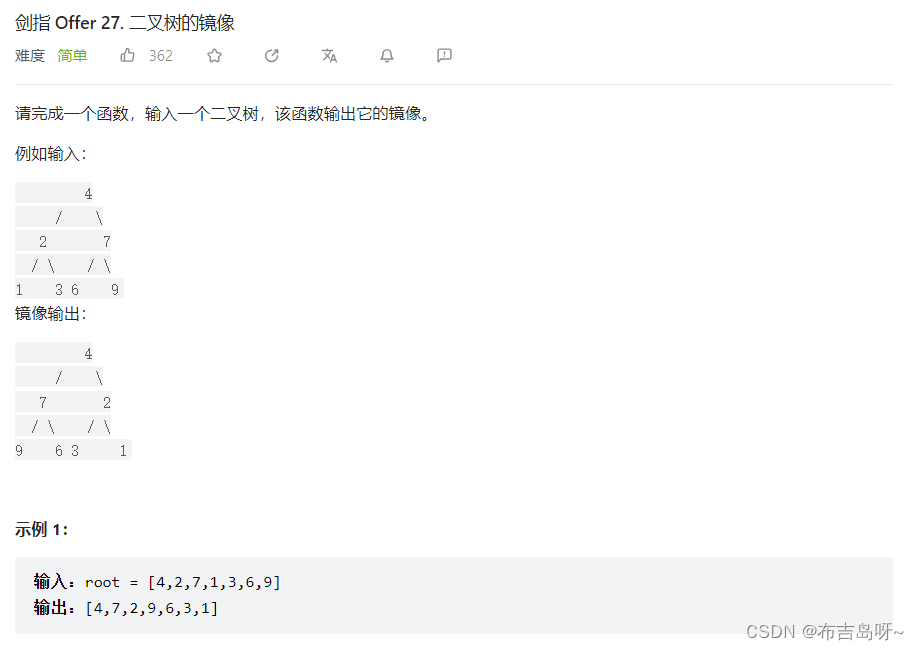
4.分割DP
对于分割类型题,动态规划的状态转移方程通常并不依赖相邻的位置,而是依赖于满足分割
条件的位置。
1)
力扣 https://leetcode.cn/problems/perfect-squares/举个例子对于8来说,要计算
完全平方数的最少数量 ,需要依次遍历:8-1*1, 8-2*2这两个数的
完全平方数的最少数量 ,选择最少的那个,然后加一,就是8的
完全平方数的最少数量 。
https://leetcode.cn/problems/perfect-squares/举个例子对于8来说,要计算
完全平方数的最少数量 ,需要依次遍历:8-1*1, 8-2*2这两个数的
完全平方数的最少数量 ,选择最少的那个,然后加一,就是8的
完全平方数的最少数量 。
所以转移方程是
dp[i] = 1 + min(dp[i-1*1], dp[i-2*2], dp[i-3*3], ......dp[i-j*j]) (i-j*j>=0)
class Solution {
public:
int numSquares(int n) {
vector<int> dp(n+1,INT_MAX);
dp[0] = 0;
for(int i=1;i<=n;i++){
for(int j=1;j*j<=i;j++){
dp[i] = min(dp[i], dp[i-j*j]+1);
}
}
return dp[n];
}
};2)
力扣![]() https://leetcode.cn/problems/decode-ways/当前元素的解码方法,取决于当前元素和前一个元素
https://leetcode.cn/problems/decode-ways/当前元素的解码方法,取决于当前元素和前一个元素
如果结合起来是一个11到26之间的数字 ,那说明当前元素有两种解码方法,一种是与前一个元素结合,一种是独立成为一个数字
如果结合起来是10,那说明当前元素只有一种解码方法,就是与前一个元素结合,因为0不能独立存在
如果结合起来是一个不在10到26之间的数字,那说明当前元素只有一种解码方法,就是独立成为一个数字
除此之外,再考虑一下不存在解码方法的情况就可以了。
class Solution {
public:
int numDecodings(string s) {
int n = s.size();
vector<int> dp(n+1,1);
if((s[0]-'0')==0) return 0;
if(n<2) return n;
int pre = s[0]-'0';
for(int i=2;i<=n;i++){
int cur = s[i-1] - '0';
if((pre==0||pre>2)&&cur==0){
return 0;
}
if((pre==1)||(pre==2 && cur<7)){
if(cur==0){
dp[i] = dp[i-2];
}else{
dp[i] = dp[i-1] + dp[i-2];
}
}else{
dp[i] = dp[i-1];
}
pre = cur;
}
return dp[n];
}
};3)
力扣![]() https://leetcode.cn/problems/word-break/
https://leetcode.cn/problems/word-break/
这道题比较清晰,每当子串与字典中的词相等时,当前的状态就会等于字符串中减掉字串的坐标的状态。这样两重遍历后,就可以得到结果。
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
int n = s.size();
vector<bool> dp(n+1, false);
dp[0] = true;
for(int i=1;i<=n;i++){
for(string w:wordDict){
int len = w.length();
if(i>=len && s.substr(i-len, len)==w){
dp[i] = dp[i] || dp[i-len];
}
}
}
return dp[n];
}
};