一、前言
DCT变换(离散余弦变换) 是数字图像处理过程中广泛采用的一种操作,用于将空域的图像转换为频域表示,从而能够更有效地进行压缩、滤波和特征提取等处理。它在许多应用领域中发挥着重要的作用,尤其在图像和视频压缩中,DCT变换常被用作预处理步骤。
例如在JPEG压缩中,一个关键步骤就是应用DCT变换。通过将图像划分为小的图像块,并对每个块进行DCT变换,可以将图像转换为频域表示。DCT变换能够将图像中的能量集中在较低频率分量上,这样就可以利用量化技术对高频分量进行更有效的压缩,从而实现较高的压缩比。
现在,介绍一种简单而有效的矩阵运算方法来实现DCT变换。
二、方法介绍
第一步:图像分块,将图像分成8×8的块。假设,现处理的图像块数据如下:
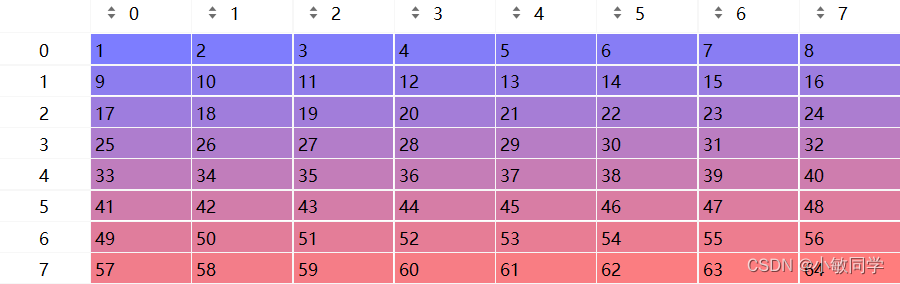
第二步:根据公式,计算DCT系数。算得,DCT系数矩阵如下:
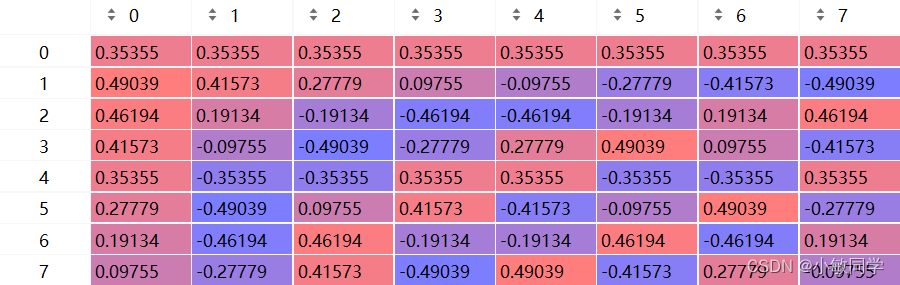
第三步:通过矩阵乘法实现每个图像块的DCT变换。流程如下:
首先,按照矩阵乘法规则,计算DCT系数矩阵×图像块矩阵

然后,将上述步骤得到的结果矩阵×DCT系数矩阵的转置矩阵

最后,得到该图像块的DCT变换结果
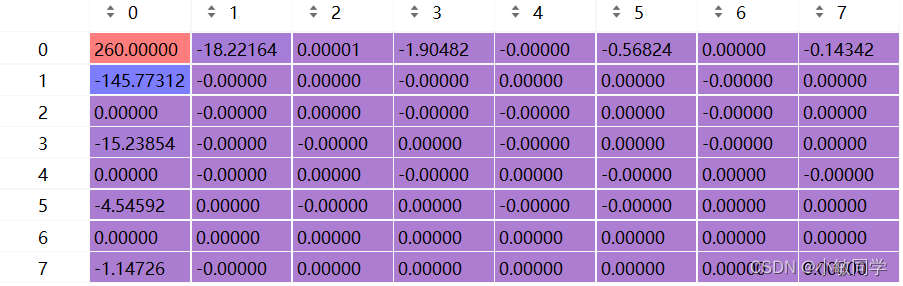
三、程序实现
import torch
import numpy as np
# 1.构造图像块伪数据
image = torch.arange(1, 65).reshape(1, 1, 8, 8)
image_dct_int = torch.cat(torch.cat(image.split(8, 2), 0).split(8, 3), 0)
image_dct = image_dct_int.float()
print("原始图像块:\n", image_dct)
# 2. 构造DCT变换系数
coff = torch.zeros((8, 8), dtype=torch.float)
coff[0, :] = 1 * np.sqrt(1 / 8)
for i in range(1, 8):
for j in range(8):
coff[i, j] = np.cos(np.pi * i * (2 * j + 1) / (2 * 8)) * np.sqrt(2 / 8)
# 3. 执行DCT变换
image_dct = torch.matmul(coff, image_dct)
coff_permute = coff.permute(1, 0)
image_dct1 = torch.matmul(image_dct, coff_permute)
image_dct2 = torch.cat(torch.cat(image_dct1.chunk(1, 0), 3).chunk(1, 0), 2)
print("DCT变换后的结果:\n", image_dct2)
四、对比验证
这里我们采用OpenCV的库函数实现同样的DCT变换,将其与以上结果进行对比验证。
import numpy as np
import cv2
image = np.arange(1, 65).reshape(8, 8)
image = np.float32(image)
print("原始图像块数据:\n", image)
dct_array = cv2.dct(image)
print("DCT变换结果:\n", dct_array)
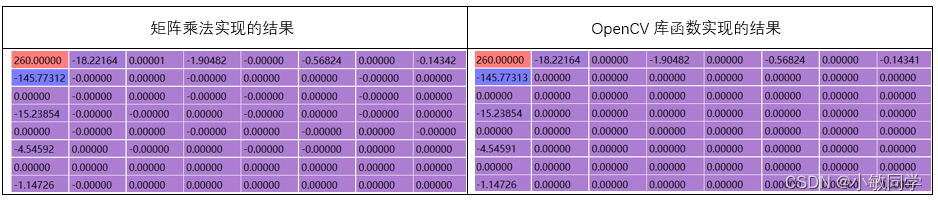
由上表可见,两种方式的计算结果都是相同的。因此,根据以上所介绍的方法,也能够正确实现图像块的DCT变换。