1.感知机(Perceptron)的原理及实现
声明:笔记来源于《白话机器学习的数学》
感知机是接受多个输入后将每个值与各自权重相乘,最后输出总和的模型。
单层感知机因过于简单,无法应用于实际问题,但它是神经网络和深度学习的基础模型。
单层感知机指的是感知机、多层感知机指的是神经网络(之前本人相关笔记:机器学习和AI底层逻辑、深度神经网络底层原理、卷积神经网络底层原理)
w ⋅ x = ∑ i = 1 n w i x i \boldsymbol{w}\cdot\boldsymbol{x}=\sum_{i=1}^{n}w_ix_i w⋅x=i=1∑nwixi

感知机的缺点是只能解决线性可分的问题

1.1 使用向量内积来表达直线(分类边界)
权重向量中的各个值就是我们说的未知参数
如何使用向量内积来表达直线?
向量内积衡量的是两个向量的相似程度
利用内积为0,则两个向量垂直,其中一个向量为权重向量,另一个向量所在的直线则可表示分类边界
假设权重向量
w
=
(
1
,
1
)
w=(1,1)
w=(1,1)

移项后为
x
2
=
−
x
1
x_2=-x_1
x2=−x1,
x
2
x_2
x2为纵轴、
x
1
x_1
x1为横轴

我们观察一下分类边界的两侧对应内积的情况
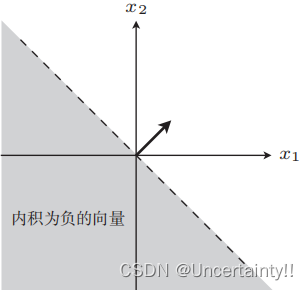 图1 内积为负 图1 内积为负
|
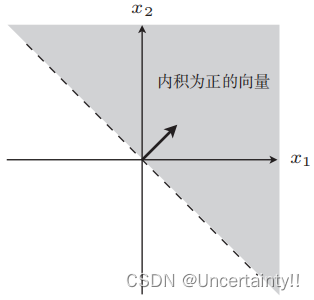 图2 内积为正 图2 内积为正
|
为什么是这种结果的呢?
w
⋅
x
=
∣
w
∣
⋅
∣
x
∣
cos
θ
\boldsymbol{w}\cdot\boldsymbol{x}=|\boldsymbol{w}|\cdot|\boldsymbol{x}|\cos\theta
w⋅x=∣w∣⋅∣x∣cosθ
其中
∣
w
∣
、
∣
x
∣
|\boldsymbol{w}|、|\boldsymbol{x}|
∣w∣、∣x∣均为正数,
若
w
⋅
x
<
0
\boldsymbol{w}\cdot\boldsymbol{x}\lt 0
w⋅x<0,则
cos
θ
<
0
\cos\theta\lt 0
cosθ<0,即
θ
\theta
θ范围为
[
90
°
,
180
°
]
[90°,180°]
[90°,180°],与权重向量夹角在此范围的内积为负
若
w
⋅
x
>
0
\boldsymbol{w}\cdot\boldsymbol{x}\gt 0
w⋅x>0,则
cos
θ
>
0
\cos\theta\gt 0
cosθ>0,即
θ
\theta
θ范围为
[
0
°
,
90
°
]
∪
[
270
°
,
360
°
]
[0°,90°]\cup[270°,360°]
[0°,90°]∪[270°,360°],与权重向量夹角在此范围的内积为正
上图中的两个范围作为两个类别,那一条直线就是分类边界,这个分类边界由权重向量表示
在权重向量已知的情况下(权重向量需要我们通过训练来得到),我们将数据代入,判断内积的正负即可完成分类的任务
我们为内积为负的区域类别设置标签为-1,为内积为正的区域类别设置标签为1

1.2 权重向量的更新表达式
f w ( x ( i ) ) f_{\boldsymbol{w}}(\boldsymbol{x}^{(i)}) fw(x(i))为判别函数、 y ( i ) y^{(i)} y(i)为对应的标签,标签代表该数据在哪个分类(可能是人工标注)
如果
f
w
(
x
(
i
)
)
≠
y
(
i
)
f_{\boldsymbol{w}}(\boldsymbol{x}^{(i)})\neq y^{(i)}
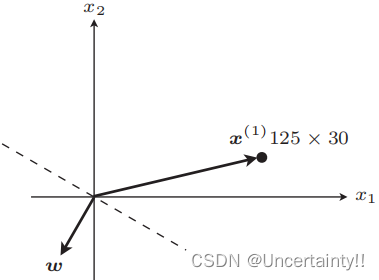
fw(x(i))=y(i)表示分类失败,例如某些应该在内积为负区域的值落在了正区域,则需要更新权重向量(图像上表现为权重向量的旋转)
如果
f
w
(
x
(
i
)
)
=
y
(
i
)
f_{\boldsymbol{w}}(\boldsymbol{x}^{(i)})= y^{(i)}
fw(x(i))=y(i)表示分类成功,则无需更新权重向量(位置保持不变)


| 
|
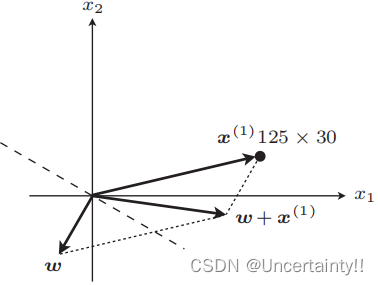
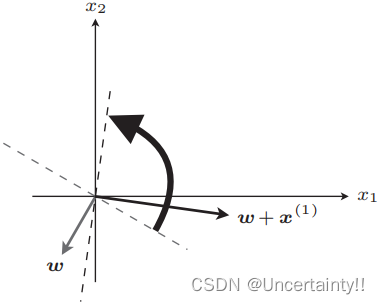
| 
|

旋转权重向量后,该数据判别结果与标签相等,分类成功,代入所有数据使得权重向量最终在这些数据的正确位置,其法线向量所在直线为分类边界
1.2 感知机(Perceptron)的实现
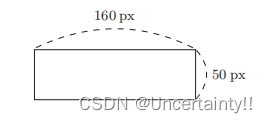
输入图像水平方向和竖直方向的像素,判断该图像是纵向的还是横向的?
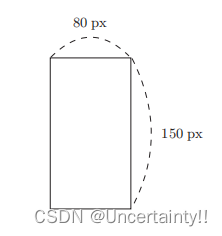
| 
|
x
1
x1
x1为水平方向像素、
x
2
x2
x2为竖直方向像素、
y
y
y为标签,
y
=
−
1
y=-1
y=−1代表该图像为纵向的,
y
=
1
y=1
y=1代表该图像为横向的

import numpy as np
import matplotlib.pyplot as plt
# 读入训练数据
train = np.loadtxt('~/Downloads/sourcecode-cn/images1.csv', delimiter=',', skiprows=1)
train_x = train[:,0:2]
train_y = train[:,2]
绘制训练数据
plt.plot(train_x[train_y == 1, 0], train_x[train_y == 1, 1], 'o')
plt.plot(train_x[train_y == -1, 0], train_x[train_y == -1, 1], 'x')
plt.axis('scaled')
plt.show()
x
1
x_1
x1为
x
x
x 轴,
x
2
x_2
x2为
y
y
y 轴

# 权重初始化
w = np.random.rand(2)
w = [ w 1 w 2 ] \boldsymbol{w}=\left [ \begin{matrix} w_1 \\ w_2 \\ \end{matrix} \right ] w=[w1w2]
# 判别函数
def f(x):
if np.dot(w, x) >= 0:
return 1
else:
return -1

# 重复次数
epoch = 10
# 更新次数
count = 0
感知机停止学习的标准最好根据精度来决定是否停止,我们这里暂时通过规定迭代次数作为循环的结束条件
# 学习权重
for _ in range(epoch):
for x, y in zip(train_x, train_y):
if f(x) != y:
w = w + y * x
# 输出日志
count += 1
print('第 {} 次 : w = {}'.format(count, w))


# 绘图确认
x1 = np.arange(0, 500)
plt.plot(train_x[train_y == 1, 0], train_x[train_y == 1, 1], 'o')
plt.plot(train_x[train_y == -1, 0], train_x[train_y == -1, 1], 'x')
plt.plot(x1, -w[0] / w[1] * x1, linestyle='dashed')
plt.show()
使权重向量成为法线向量的直线方程是内积为 0 的 x 的集合


验证