分割回文串-ii
题目链接:分割回文串-ii
思路:分割字符串s,使得子串都是回文串,最后获得最小分割次数。那么我们可以不断把字符串缩短,判断子串是否可以被分割成回文串,并且最小分割次数。这就是子问题分割了。所以我们可以使用动态规划。
状态:F(i):字符串s的前i个字符组成的子串的
最小分割次数
状态转移方程:
F(i):min(F(i),F(j)+1);j<i && s[j]~s[i] 是回文串
如果s[j]~s[i] 是回文串,因为要取最小分割次数,所以是F(i)当前分割次数和F(j)+1(前 j 个字符的分割次数+1)比较
而且每一次递推开始时,我们可以先判断当前子串自身是否是回文串,如果是,F(i) = 0,即不用分割
代码如下:
//判断字符串是否是回文串
bool Ispalindrome(string&& str)
{
int left = 0;
int right = str.size() - 1;
while (left < right)
{
if (str[left] != str[right])
return false;
++left;
--right;
}
return true;
}
//主函数
int minCut(string s)
{
//准备一个存放分割次数的数组,并都初始化为int的最大值
//因为0号字符串是不需要分割,即本身回文,所以0号位置不需要
//所以需要准备size+1个位置
vector<int>dp(s.size() + 1,INT_MAX);
//因为substr函数是左闭右开,所以要遍历到size位置
for (int i = 1; i <= s.size(); ++i)
{
//先判断当前子串是否是回文
if(Ispalindrome(string(s.substr(0,i))))
{
dp[i]=0;
continue;
}
//再分子串判断
for (int j = 1; j < i; ++j)
{
if (Ispalindrome(string(s.substr(j, i-j))))
dp[i] = min(dp[j] + 1,dp[i]);//取最小
}
}
return dp[s.size()];
}
优化:当前代码的时间复杂度时n^3:i,j循环+检查回文串
我们可以直接将所有检查回文子串的结果放到二维数组中,以空间换时间,时间复杂度就到了n^2
子状态:从第一个字符到第二个字符是不是回文串,第1-3,2-5…
F(i,j):字符区间[i,j]是否是回文串
状态转移方程:F(i,j)有三种情况
- i==j时,代表只有一个字符,此时是回文的
- i+1==j时,代表有两个字符,此时需要判断s[i] == s[j]
- 其他情况,需要先判断s[i]==s[j],如果是相同的,那么再根据F[i+1][j-1],即往中间缩短的字符串是否是回文串
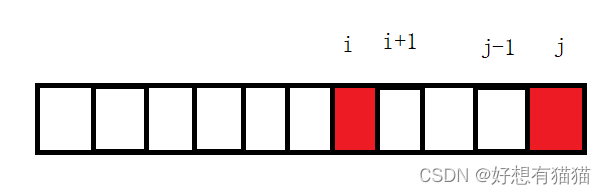
因为要依赖F[i+1][j-1]的结果,所以二维数组的更新是从右下角开始,并且是一个上对角矩阵

代码如下:
//动态规划的判断回文串
vector<vector<bool>> palindrome(string s)
{
int n=s.size();
vector<vector<bool>> pal(n,vector<bool>(n,false));
//从最后一行开始更新
for(int i=n-1;i>=0;--i)
{
for(int j=i;j<n;++j)
{
if(i==j)
pal[i][j]=true;
else if(i+1==j)
pal[i][j]=(s[i]==s[j]);
else
pal[i][j]=(s[i]==s[j])&&(pal[i+1][j-1]);
}
}
return pal;
}
int minCut(string s)
{
vector<int>dp(s.size() + 1);
//dp数组要初始化
//每个子串分割的最大次数就是下标-1
//[0]号位置必须被初始化为-1
//因为"aaaaa"这样的子串最小分割次数是-1+1=0
for(int i=0;i<=s.size();++i)
dp[i]=i-1;
//获取回文子串的二维数组
vector<vector<bool>> pal=palindrome(s);
//要遍历到size位置
for (int i = 2; i <= s.size(); ++i)
{
for (int j = 0; j < i; ++j)
{
//第j~i-1的子串是否是回文串
if (pal[j][i-1])
dp[i] = min(dp[j] + 1,dp[i]);//取最小
}
}
return dp[s.size()];
}