一、选择填空判断题

题1

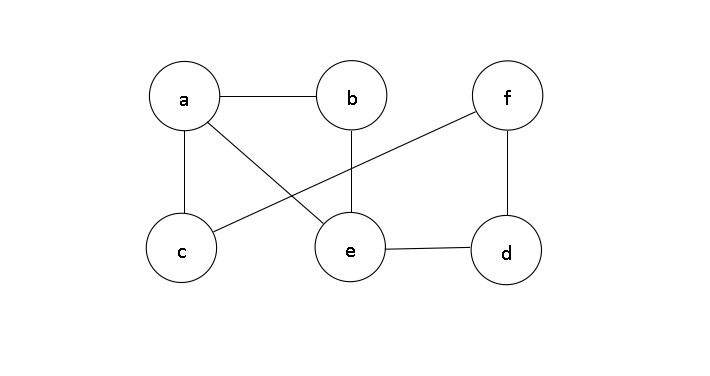
1、无向图G=（V，E），其中：V={a，b，c，d，e，f}，E={（a，b），（a，c），（a，e），（b，e），（c，f），（f，d），（e，d）}，以顶点a为源点对该图进行深度优先遍历，得到的顶点序列正确的是（）。
A、a，b，e，c，d，f
B、a，c，f，e，b，d
C、a，e，b，c，f，d
D、a，e，d，f，c，b

解析：（D）
如下可画出该无向图：

图的深度优先搜索（DFS）【类似树的先序遍历，先访问结点，然后递归向外层结点遍历，尽可能深地搜索一个图，都采用回溯算法】。
DFS算法是一个递归过程，其中需借助栈完成操作。首先选取图中某一顶点vi，访问后，任意选取一个与vi邻接的顶点，且该顶点未被访问，……，继续重复该过程，直到图中所有与vi连通的顶点都被访问到；若还有顶点未被访问到，则另外选取一个未被访问的顶点再次作为起始点，重复以上步骤，继续直至图中所有结点被访问。

以顶点a为源点对该图进行深度优先遍历，然后选择与a邻接的任一顶点，由于与a邻接的顶点有b，c，e，可有以下三种访问序列{a，b，……}或{a，c，……}或{a，e，……}，

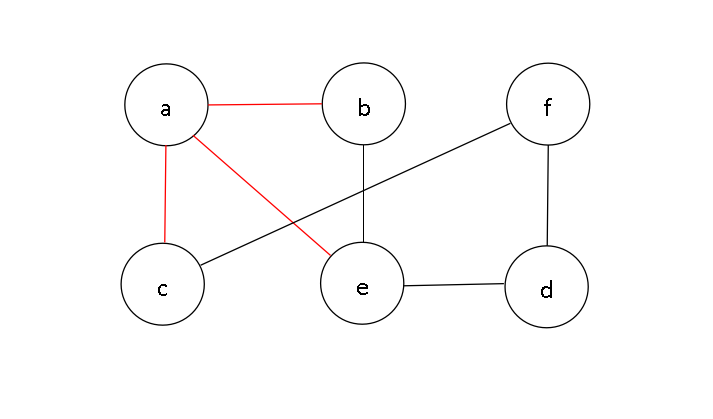
然后，选择访问顶点d，也可以选择还未被访问的顶点。由于先前选择访问的序列是{a，d}，此时访问与顶点d相邻的顶点f，得到序列{a，d，f}；再访问与顶点f相邻的顶点c，得到序列{a，d，f，c}；由于此时与c邻接的顶点a和f都被访问过，回退到f，继续检查d，与d邻接的顶点也被访问过，……，最后直到顶点d还未被访问，访问它，可得到序列{a，e，d，f，c，b}。

题2

2、如下所示的图进行从顶点1开始的广度优先搜索遍历，可得到的顶点访问序列为（）。
A、1，3，2，4，5，6，7
B、1，2，4，3，5，6，7
C、1，2，3，4，5，7，6
D、2，5，1，4，7，3，6

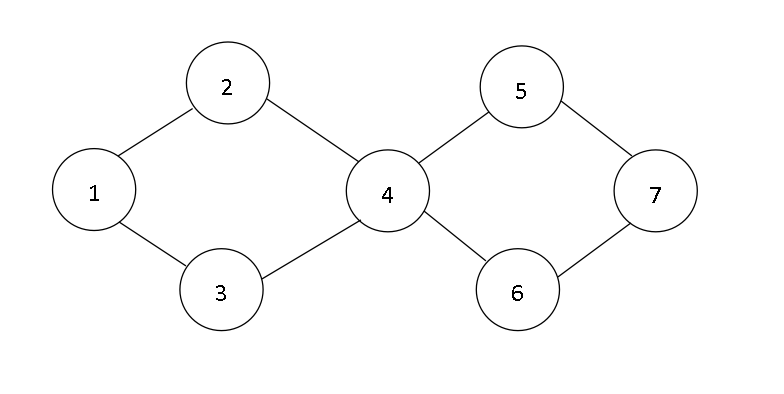
解析：（B）
图的广度优先搜索（BFS）【类似树的层序遍历，一层一层向外遍历】。
首先选取一个起始点顶点vi，访问后将其入队并标记为已访问（使用队列用于避免重复访问，存放已经访问过的各邻接顶点）；当队列不为空时检查出队顶点的所有邻接顶点，访问未被访问的邻接顶点并将其入队，……，继续重复该过程，直到图中所有与vi连通的顶点都被访问到；当队列为空时跳出循环，则此时遍历完成。

以顶点1为源点对该图进行广度优先遍历，选择与其邻接的所有顶点进行访问，有2和3，可得序列{1，2，3}或{1，3，2}；然后，再访问与2和3邻接的其他顶点，直到所有顶点被访问。例如，选择访问顶点2，然后访问与顶点2邻接的4；此时访问顶点4的邻接顶点，由于顶点2已经被访问，可选择访问顶点3和顶点5和顶点6，选择顶点3，此时的序列为{1，2，4，3}；再访问与顶点4邻接的顶点5和6，序列为{1，2，4，3，5，6}；最后还有顶点7还未访问，可得序列{1，2，4，3，5，6，7}。

题3

3、具有n个顶点的有向完全图有（）条边。
A、n（n-1）/2
B、n（n-1）
C、n（n+1）/2
D、n（n+1）

解析：（B）
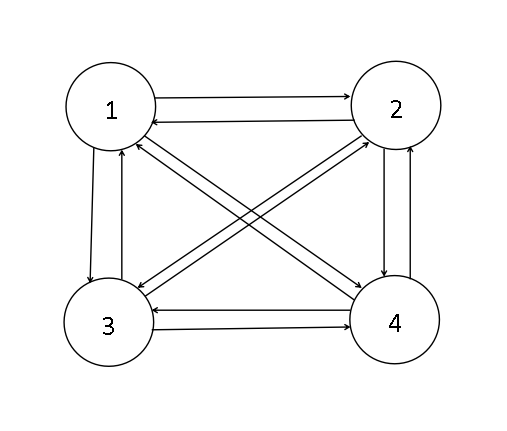
若一个有向图中，若每个顶点都有互相相反的两条弧连接，则称为有向完全图，在一个含有n个顶点的有向完全图中，共有n(n-1)条弧。

例如，含有4个顶点的有向完全图中，共有n(n-1)=4×3=12条弧，如下：

二、应用题

题1

题型：根据图的邻接表存储结构，画出图以及图的深度/广度优先生成树

1、设G=（V，E）以邻接表存储，如下图所示，画出该图的深度优先生成树和广度优先生成树。

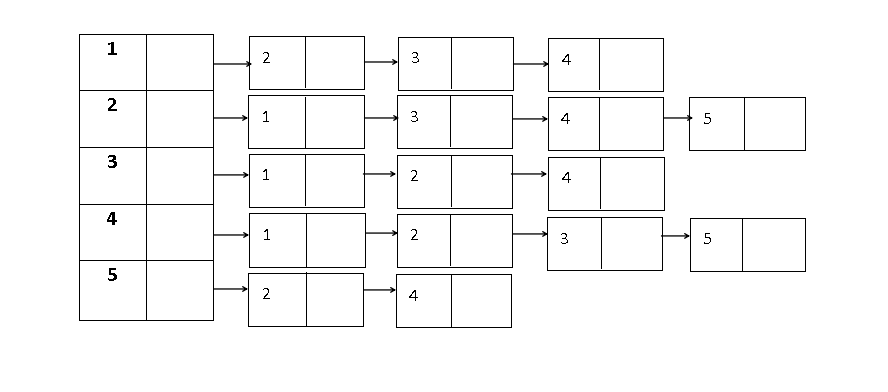
解：由该邻接表可知，顶点1与2，3，4邻接，顶点2与1，3，4，5邻接，顶点3与1，2，4邻接，顶点4与1，2，3，5邻接，顶点5与2，4邻接，画出该图：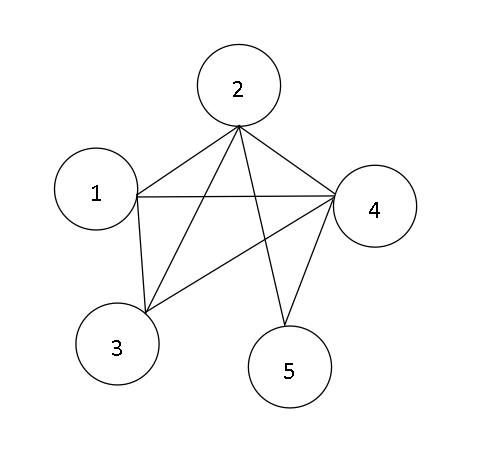
图的深度优先遍历序列步骤：
1、首先访问顶点1，访问后标记已访问过，此时序列为{1}；
2、查看单链表1，其第一个未访问的邻接顶点为2，再以顶点2为出发点继续深度遍历，此时序列为{1，2}；
3、查看单链表2，顶点1已经访问过，所以其未访问的邻接顶点为3，再以顶点3为出发点继续深度遍历，此时序列为{1，2，3}；
4、查看单链表3，顶点1和顶点2已经访问过，所以其未访问的邻接顶点为4，再以顶点4为出发点继续深度遍历，此时序列为{1，2，3，4}；
5、查看单链表4，顶点1、顶点2、顶点3已经访问过，所以其未访问的邻接顶点为5，再以顶点5为出发点继续深度遍历，此时序列为{1，2，3，4，5}；
6、已经不存在未访问的顶点，遍历完成。

图的广度优先遍历序列步骤：
1、首先访问顶点1，访问后标记已访问过，使其入队，然后删除当前队头结点，此时序列为{1}；
2、遍历单链表1，使其未访问的邻接顶点2、3、4入队并标记，此时序列为{1，2，3，4}；
3、遍历单链表2，使其未访问的邻接顶点5入队并标记，此时序列为{1，2，3，4，5}；
4、已经不存在未访问的顶点，遍历完成。

深度优先生成树：

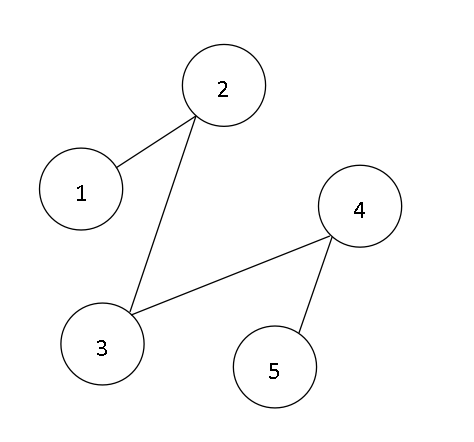
广度优先生成树：