交叉熵、Focal Loss以及其Pytorch实现

本文参考链接：https://towardsdatascience.com/focal-loss-a-better-alternative-for-cross-entropy-1d073d92d075

一、交叉熵

损失是通过梯度回传用来更新网络参数是之产生的预测结果和真实值之间相似。不同损失函数有着不同的约束作用，不同的数据对损失函数有着不同的影响。

交叉熵是常见的损失函数，常见于语义分割、对比学习等。其函数表达式如下，其中$Y_i和p_i$分别表示真实值和预测结果：
$$CrossEntropy=-\sum _{i=1}^{i=n}{Y}_{i}log(p_i)$$
因为$p_i$值在0~1之间，故交叉熵大于等于0。这个函数什么时候最小呢？数学证明结果表明当$Y_i=p_i$时交叉熵最小。下面，我们取二分类情况来进行简单证明：
$$BCELoss=-ylogx-(1-y)log(1-x)$$
对BCELoss求导可得：
$$-\frac{y}{x}+\frac{1-y}{1-x}=\frac{y-x}{x-x^2}$$
所以当$y=x$时，二分类交叉熵取最小值。

那么，交叉熵有啥子问题？

• 从表达式可以看出，交叉熵只针对单个像素进行比较，像素和像素之间并没有联系，这就需要我们在模型中使用空间注意力机制等使得特征在空间上进行交互。针对这个问题，不少论文提出了改进方案，如Context Prior for Scene Segmentation这篇论文就使用了和precision、recall等类似的损失函数（就像Dice loss和F1 score指标一样）。

• 类别不平衡：这个问题比较常见，语义分割中类别在图片上总像素占比是不平衡。如果类别不平衡比较严重，交叉熵损失就会偏向于占比较高的类别，导致对占比较少的类别预测结果较差。解决这一方法为给交叉熵损失添加权重（平衡交叉熵）等，如下式：
  $$BalancedCrossEntropy=-\sum _{i=1}^{i=n}{\alpha }_i{Y}_{i}log(p_i)$$

• 困难样本：首先，我们要知道困难样本是那些模型反复出现巨大损失的例子，而简单样本是那些容易分类的例子。交叉熵对于所有样本同等对待，导致无法辨别困难样本和简单样本。解决这一问题就是接下来的损失函数Focal loss

二、Focal loss

Focal loss关注的是模型出错的例子，而不是它可以自信地预测的例子，确保对困难的例子的预测随着时间的推移而改善，而不是对容易的例子变得过于自信。

这到底是怎么做到的呢？Focal loss是通过一个叫做Down Weighting的东西来实现的。下调权重是一种技术，它可以减少容易的例子对损失函数的影响，从而使人们更加关注困难的例子。这种技术可以通过在交叉熵损失中加入一个调节因子来实现。其表达式如下：
$$FocalLoss=-\sum _{i=1}^{i=n}(1-p_i{)}^{\gamma }log{p}_i$$
不同的$\gamma$对损失有什么影响呢？如下图所示

不同的$\gamma$对$(1-p_i{)}^{\gamma }$有什么影响呢，如下：

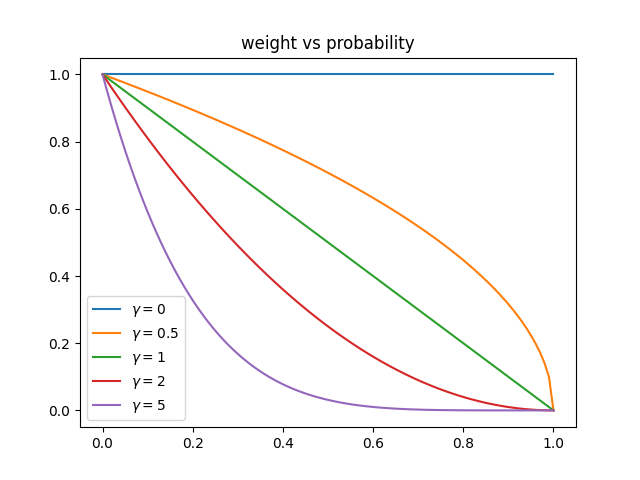
• 在误分类样本的情况下，$pi$很小，使得调制因子大约或非常接近于1，这使损失函数不受影响。此时，Focal Loss和交叉熵损失相似。
• 随着模型置信度的提高，即$pi\to 1$，调制因子将趋于0，从而降低了分类良好的例子的损失值。聚焦参数，$\gamma$≥1，将重新调整调制因子，使容易的例子比困难的例子降权更多，减少它们对损失函数的影响。例如，考虑预测概率为0.9和0.6。考虑到$\gamma$=2，对0.9计算出的损失值是4.5e-4，降权系数($1/(1-q_i{)}^2$)为100，对0.6则是3.5e-2，降权系数为6.25。从实验来看，$\gamma$=2来说效果最好。
• 当$\gamma$=0时，Focal Loss等同于Cross Entropy。

此外，加入平衡因子$\alpha$，用来平衡正负样本本身的比例不均：文中$\alpha$取0.25，即正样本要比负样本占比小，这是因为负例易分。其表达式如下：
$$FocalLoss=-\sum _{i=1}^{i=n}{\alpha }_i(1-p_i{)}^{\gamma }log{p}_i$$
Focal Loss自然地解决了阶级不平衡的问题，(1因为来自多数类别的例子通常容易预测，而来自少数类别的例子由于缺乏数据或来自多数类别的例子在损失和梯度过程中占主导地位而难以预测。由于这种相似性，Focal Loss可能能够解决这两个问题。

三、Pytorch

1.交叉熵

2.Focal loss

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable

class FocalLoss(nn.Module):
    def __init__(self, gamma=0, alpha=None, size_average=True):
        super(FocalLoss, self).__init__()
        self.gamma = gamma
        self.alpha = alpha
        if isinstance(alpha,(float,int,long)): self.alpha = torch.Tensor([alpha,1-alpha])
        if isinstance(alpha,list): self.alpha = torch.Tensor(alpha)
        self.size_average = size_average

    def forward(self, input, target):
        if input.dim()>2:
            input = input.view(input.size(0),input.size(1),-1)  # N,C,H,W => N,C,H*W
            input = input.transpose(1,2)    # N,C,H*W => N,H*W,C
            input = input.contiguous().view(-1,input.size(2))   # N,H*W,C => N*H*W,C
        target = target.view(-1,1)

        logpt = F.log_softmax(input)
        logpt = logpt.gather(1,target)
        logpt = logpt.view(-1)
        pt = Variable(logpt.data.exp())

        if self.alpha is not None:
            if self.alpha.type()!=input.data.type():
                self.alpha = self.alpha.type_as(input.data)
            at = self.alpha.gather(0,target.data.view(-1))
            logpt = logpt * Variable(at)

        loss = -1 * (1-pt)**self.gamma * logpt
        if self.size_average: return loss.mean()
        else: return loss.sum()