【C/C++数据结构】链表与快慢指针

news2024/11/24 16:59:45

目录

一、单链表

二、双向循环链表

三、判断链表是否带环

四、链表的回文结构判断

五、复制带随机指针的链表

一、单链表

优点：头部增删效率高，动态存储无空间浪费

缺点：尾部增删、遍历效率低，不支持随机访问节点

头结点：单链表头结点可有可无，带头结点更方便进行初始化

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>

typedef int NodeData;

typedef struct List 
{
    NodeData data;
    struct List* next;
}List;

void Init(List* list) 
{
    assert(list);
    list->next = (List*)malloc(sizeof(List));    // 空头结点
    list->next->next = NULL;
}

bool Empty(List* list) 
{
    assert(list);
    return list->next->next == NULL;
}

void Push(List* list, NodeData x) 
{
    assert(list);
    List* node = (List*)malloc(sizeof(List));
    if (node == NULL) 
    {
        perror("malloc");
        return;
    }
    node->data = x;
    node->next = list->next->next;
    list->next->next = node;
}

void Pop(List* list) 
{
    assert(list);
    if (!Empty(list)) 
    {
        List* cur = list->next->next;
        list->next = cur->next;
        free(cur);
        cur = NULL;
    }
}

size_t Size(List* list) 
{
    assert(list);
    size_t size = 0;
    List* cur = list->next->next;
    while (cur) 
    {
        ++size;
        cur = cur->next;
    }
    printf("the list size = %d\n", size);
    return size;
}

void PrintList(List* list) 
{
    assert(list);
    if (!Empty(list)) 
    {
        List* cur = list->next->next;
        printf("%d ", cur->data);
        while (cur->next) 
        {
            printf("-> %d ", cur->next->data);
            cur = cur->next;
        }
        printf("\n");
    }
}

int main() 
{
    List list;
    Init(&list);
    Push(&list, 1);
    Push(&list, 3);
    Push(&list, 5);
    Push(&list, 7);
    Size(&list);
    PrintList(&list);
    Pop(&list);
    Pop(&list);
    Pop(&list);
    Pop(&list);
    Pop(&list);
    Size(&list);
    PrintList(&list);
    return 0;
}

二、双向循环链表

特征：

  • 每个Node都有一个data值，一个prev前驱指针和一个next后置指针
  • C++的STL中封装的就是双向循环链表
  • 头部增删和尾部增删效率一样高，但依然不支持随机访问
  • 链表循环且带头结点，最后一个Node指向头结点，头结点也指向最后一个Node
  • 空链表的前驱和后置指针都指向头结点，头结点不存放数据

代码分析：

Push和Pop函数通过调用Insert和Erase函数对Node进行按址增删，减少了代码的复用

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>

typedef int NodeData;

typedef struct List 
{
    NodeData data;
    struct List* prev;
    struct List* next;
}List;

void Init(List* list) 
{
    assert(list);
    list->prev = list;
    list->next = list;
}

bool Empty(List* list) 
{
    assert(list);
    return list->next == list;
}

void Insert(List* list, NodeData x, List* pos) 
{
    assert(list && pos);
    List* prev = pos->prev;
    List* node = (List*)malloc(sizeof(List));
    if (node == NULL) 
    {
        perror("malloc");
        exit(1);
    }
    node->data = x;
    node->next = pos;
    pos->prev = node;
    node->prev = prev;
    prev->next = node;
}

void Erase(List* list, List* pos) 
{
    assert(list && pos);
    List* prev = pos->prev;
    List* next = pos->next;
    prev->next = next;
    next->prev = prev;
    free(pos);
    pos = NULL;
}

void PushFront(List* list, NodeData x) 
{
    assert(list);
    Insert(list, x, list->next);
}

void PushBack(List* list, NodeData x) 
{
    assert(list);
    Insert(list, x, list);
}

void PopFront(List* list) 
{
    assert(list);
    Erase(list, list->next);
}

void PopBack(List* list) 
{
    assert(list);
    Erase(list, list->prev);
}

size_t Size(List* list) 
{
    assert(list);
    size_t size = 0;
    List* cur = list->next;
    while (cur != list) 
    {
        ++size;
        cur = cur->next;
    }
    printf("the list size is %d\n", size);
    return size;
}

void PrintList(List* list) 
{
    assert(list);
    if (!Empty(list)) 
    {
        List* cur = list->next;
        printf("%d ", cur->data);
        while (cur->next != list) 
        {
            printf("-> %d ", cur->next->data);
            cur = cur->next;
        }
        printf("\n");
    }
}

int main() 
{
    List list;
    Init(&list);
    PushFront(&list, 1);
    PushFront(&list, 3);
    PushFront(&list, 5);
    PushBack(&list, 2);
    PushBack(&list, 4);
    PushBack(&list, 6);
    Size(&list);
    PrintList(&list);   //5 -> 3 -> 1 -> 2 -> 4 -> 6

    PopFront(&list);
    PopBack(&list);
    PopBack(&list);
    PushFront(&list, 10);
    PushBack(&list, 20);
    Size(&list);
    PrintList(&list);   //10 -> 3 -> 1 -> 2 -> 20
    return 0;
}

三、判断链表是否带环

链表带环：尾结点指向链表的某个节点

函数设计：设置快慢指针，根据链表头结点head，判断链表是否带环，返回bool值

bool IsCircle(struct ListNode* head) 
{
    struct ListNode* fast = head;
    struct ListNode* slow = head;
    while (fast && fast->next) 
    {
        fast = fast->next->next;
        slow = slow->next;
        if (fast == slow) 
            return true;
    }
    return false;
}

四、链表的回文结构判断

函数要求：时间复杂度为O(n), 额外空间复杂度为O(1), 返回bool值

函数设计：

  1. 用快慢指针找到链表中间节点
  2. 将中间节点之后的链表逆置
  3. 设置头指针和中间节点指针进行回文判断
  4. 将中间节点之后的链表再次逆置, 还原链表结构
struct ListNode* MidNode(struct ListNode* head) 
{
    struct ListNode* fast = head;
    struct ListNode* slow = head;
    while (fast && fast->next) 
    {
        fast = fast->next->next;
        slow = slow->next;
    }
    return slow;
}

struct ListNode* ReverseList(struct ListNode* head) 
{
    struct ListNode* p1 = NULL;
    struct ListNode* p2 = head;
    struct ListNode* p3 = NULL;
    if (p2 != NULL) 
        p3 = head->next;
    while (p3) 
    {
        p2->next = p1;
        p1 = p2;
        p2 = p3;
        p3 = p3->next;
    }
    p2->next = p1;
    p1 = p2;
    p2 = p3;
    return p1;
}

bool ChkPalindrome(struct ListNode* A) 
{
    struct ListNode* mid = MidNode(A);
    mid = ReverseList(mid);
    struct ListNode* front = A;
    struct ListNode* back = mid;
    struct ListNode* cur = back;
    int flag = 1;
    while (back && front != cur) 
    {
        if (front->val != back->val) 
        {
            flag = 0;
            break;
        }
        front = front->next;
        back = back->next;
    }
    mid = ReverseList(mid);    //再次逆置，防止链表结构被破坏
    if (flag == 0)
        return false;
    return true;
}

五、复制带随机指针的链表

函数要求：

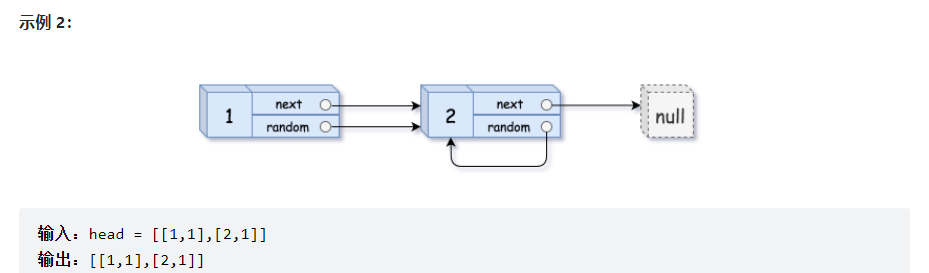
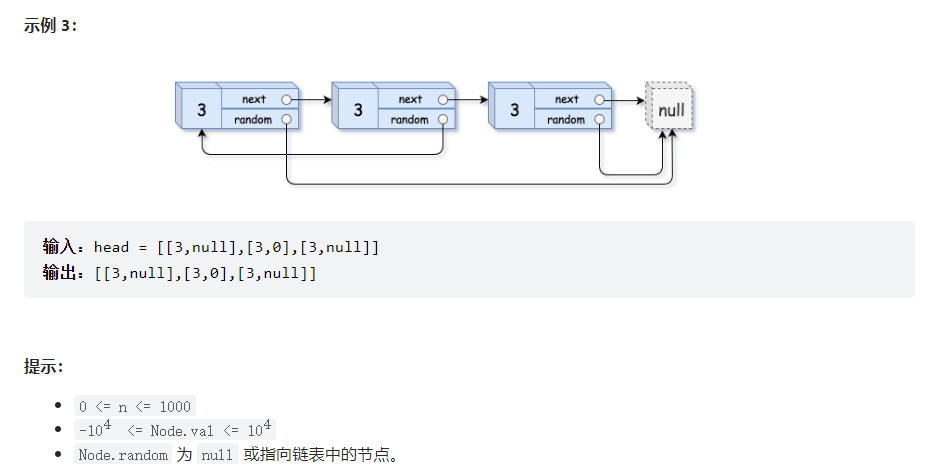
给你一个长度为 n 的链表，每个节点包含一个额外增加的随机指针 random ，该指针可以指向链表中的任何节点或空节点。

构造这个链表的深拷贝。 深拷贝应该正好由 n 个全新 节点组成，其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点，并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。

例如，如果原链表中有 X 和 Y 两个节点，其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ，同样有 x.random --> y 。

返回复制链表的头节点。

用一个由 n 个节点组成的链表来表示输入/输出中的链表。

每个节点用一个 [val, random_index] 表示：

        val：一个表示 Node.val 的整数。

        random_index：随机指针指向的节点索引（范围从 0 到 n-1）；如果不指向任何节点，则为 null 。

你的代码只接受原链表的头节点 head 作为传入参数。

函数设计：

  1. 在每个节点后面复制一个一模一样的copy节点
  2. copy->random = cur->random->next
  3. 将copy部分和原节点断开
struct Node* copyRandomList(struct Node* head) 
{
    //1. 在每个节点后面复制一个相同的节点
    struct Node* cur = head;
    if (cur == NULL) 
        return NULL;
    while (cur) 
    {
        struct Node* copy = (struct Node*)malloc(sizeof(struct Node));
        copy->val = cur->val;
        copy->next = cur->next;
        cur->next = copy;
        cur = copy->next;
    }
 
    //2. copy->random = cur->random->next
    cur = head;
    while (cur) 
    {
        struct Node* copy = cur->next;
        if (cur->random == NULL) 
            copy->random = NULL;
        else 
            copy->random = cur->random->next;
        cur = copy->next;
    }
 
    //3. 将copy部分和原链表断开
    cur = head;
    struct Node* copy = cur->next;
    struct Node* copytail = copy;
    while (cur) 
    {
        struct Node* next = copytail->next;
        cur->next = next;
        if (next) 
            copytail->next = next->next;
        cur = next;
        copytail = copytail->next;
    }
 
    return copy;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/685174.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【Linux | Shell】bash shell 基础命令

【Linux | Shell】bash shell 基础命令

目录 一、概述二、启动shell2.1 用户的默认 Shell 程序2.2 Shell 提示符 三、 基础命令3.1、man 命令3.2、cd 命令3.3、ls命令 一、概述 很多 Linux 发行版的默认 shell 是 GNU bash shell。本文将介绍 bash shell 的基本特性&#xff0c;比如 bash 手册、命令行补全以及如何显…
阅读更多...
JavaWeb 第一个Servlet程序

JavaWeb 第一个Servlet程序

1.Servlet Servlet是Java编写的用于Web应用程序的服务器端程序。 它可以接收来自Web浏览器的HTTP请求并生成响应。 Servlet通常用于创建动态Web内容&#xff0c;例如网页、表单处理、登录和数据库访问等。 Servlet是Java EE&#xff08;Enterprise Edition&#xff09;规范…
阅读更多...
[补充]托福口语21天——day2 课堂内容

[补充]托福口语21天——day2 课堂内容

day1 课堂&#xff1a;http://t.csdn.cn/cyvZm day1 语料&#xff1a;http://t.csdn.cn/syTBy 目录 1 时间准备 2 例题 3 答题步骤 3.1 范例 3.2 范例 4 连接词 5 完整回答 5.1 范例 5.2 范例 6 总结 背背背&#xff01; 1. 如今的生活成本非常高。人们要付…
阅读更多...
学习系统编程No.25【核心转储实战】

学习系统编程No.25【核心转储实战】

引言&#xff1a; 北京时间&#xff1a;2023/6/16/8:39&#xff0c;实训课中&#xff0c;大一下学期最后有课的一天&#xff0c;还有两天就要期末考啦&#xff01;目前什么都还没有复习&#xff0c;不到星期天晚上&#xff0c;咱不慌&#xff0c;小小挂科&#xff0c;岂能拦得…
阅读更多...
postgresql_internals-14 学习笔记（六）—— 统计信息

postgresql_internals-14 学习笔记（六）—— 统计信息

不完全来自这本书&#xff0c;把查到的和之前的文章重新汇总整理了一把。 一、 统计信息的收集 1. 主要参数 其中最主要的是track_counts&#xff0c;开启才会收集统计信息。 postgres# select name,setting,short_desc,context from pg_settings where name like track%; na…
阅读更多...
LeetCode 周赛 351（2023/06/25）T2 有点意思

LeetCode 周赛 351（2023/06/25）T2 有点意思

本文已收录到 AndroidFamily&#xff0c;技术和职场问题&#xff0c;请关注公众号 [彭旭锐] 和 [BaguTree Pro] 知识星球提问。 往期回顾&#xff1a;LeetCode 单周赛第 348 场 数位 DP 模版学会了吗&#xff1f; T1. 美丽下标对的数目&#xff08;Easy&#xff09; 标签&am…
阅读更多...
python爬虫并做可视化分析--前程无忧

python爬虫并做可视化分析--前程无忧

一.数据采集 1.采集逻辑 2.数据schema 招聘信息Schema { "岗位名称": "财务会计主管", "薪资":"1.3-2万", "地址": "*******", "经验要求": "5-7年", "公司名": "***…
阅读更多...
JDK8新特性-上部

JDK8新特性-上部

文章目录 一、Java发展史1.1 发展史1.2 OpenJDK和OracleJDK1.3 Open JDK 官网介绍 二、Lambda表达式2.1 需求分析2.2 Lamada表达式的体验2.3 Lambda表达式的语法规则2.3.1 Lambda表达式练习2.3.2 Lambda表达式练习 2.4 Lambda表达式的使用前提2.5 FunctionalInterface注解2.6 L…
阅读更多...
MATLAB | 如何使用MATLAB获取顶刊《PNAS》绘图(附带近3年图像)

MATLAB | 如何使用MATLAB获取顶刊《PNAS》绘图(附带近3年图像)

千呼万唤始出来&#xff0c;《PNAS》绘图获取的代码来啦&#xff0c;不过这次研究了半天也没想到如何获取付费文章的绘图&#xff0c;就只下载了免费文章(主要也怕侵权)&#xff0c;不过光免费文章的图片三年了也有接近1.7w张了&#xff0c;同时使用代码下载时依旧需要科学上网…
阅读更多...
【Redis】Redis的数据结构

【Redis】Redis的数据结构

【Redis】Redis的数据结构 文章目录 【Redis】Redis的数据结构1. 动态字符串SDS2. IntSet2.1 IntSet升级 3. Dict3.1 Dict的扩容3.2 Dict的收缩3.3 Dict的rehash 4. ZipList4.1 ZipList中的Entry4.1.1 Encoding编码 4.2 ZipList的连锁更新问题4.3 特性 5. QuickList 1. 动态字符…
阅读更多...
【软考网络管理员】2023年软考网管初级常见知识考点（7）-生成树协议

【软考网络管理员】2023年软考网管初级常见知识考点（7）-生成树协议

涉及知识点 STP的原理&#xff0c;端口的状态&#xff0c;RSTP协议&#xff0c;MSTP协议&#xff0c;软考网络管理员常考知识点&#xff0c;软考网络管理员网络安全&#xff0c;网络管理员考点汇总。 原创于&#xff1a;CSDN博主-《拄杖盲学轻声码》&#xff0c;更多考点汇总可…
阅读更多...
模拟电路系列分享-运放的关键参数2

模拟电路系列分享-运放的关键参数2

目录 概要 整体架构流程 技术名词解释 1.输入偏置电流&#xff1a; 2.输入失调电流 技术细节 总结; 概要 提示&#xff1a;这里可以添加技术概要 实际运放与理想运放具有很多差别。理想运放就像一个十全十美的人&#xff0c;他学习100 分&#xff0c;寿命无限长&#xff0c;长…
阅读更多...
Modal对话框（antd-design组件库）展示所有配置选项和onChange的作用

Modal对话框（antd-design组件库）展示所有配置选项和onChange的作用

1.Modal对话框 模态对话框。 2.何时使用 需要用户处理事务&#xff0c;又不希望跳转页面以致打断工作流程时&#xff0c;可以使用 Modal 在当前页面正中打开一个浮层&#xff0c;承载相应的操作。 另外当需要一个简洁的确认框询问用户时&#xff0c;可以使用 App.useApp 封装的…
阅读更多...
创建微信小程序的几种方式

创建微信小程序的几种方式

创建微信小程序的几种方式 1. 使用原生方式 在官网上下载微信开发者工具&#xff0c;之后使用微信开发者工具新建项目即可。 微信这边提供了多个模板&#xff0c;可以直接下载模板快速搭建上线&#xff0c;也可以使用空白模板根据需求自行编写。 空白模板项目结构&#xff1…
阅读更多...
C语言：打印0-100000中的自幂数（水仙花数是其中一种）

C语言：打印0-100000中的自幂数（水仙花数是其中一种）

题目&#xff1a; 求出 0&#xff5e;100000 之间的所有 自幂数 并输出。 自幂数是指一个n位数&#xff0c;其各位数字的n次方之和恰好等于该数本身&#xff0c; 如:153&#xff1d;1^3&#xff0b;5^3&#xff0b;3^3&#xff0c; 则153是一个自幂数。 思路&#xff1a; 总体…
阅读更多...
【数据网格架构】分布式数据网格作为集中式数据单体的解决方案

【数据网格架构】分布式数据网格作为集中式数据单体的解决方案

企业数据架构师不应构建大型集中式数据平台&#xff0c;而应创建分布式数据网格。 ThoughtWorks 的首席技术顾问 Zhamak Dehghani 在旧金山 QCon 的演讲和相关文章中表示&#xff0c;这种方法的改变需要范式转变。随着数据变得越来越普遍&#xff0c;传统的数据仓库和数据湖架构…
阅读更多...
Linux基础+命令操作+mysql、tomcat、nginx、RabbitMQ、Redis，ElasticSearch

Linux基础+命令操作+mysql、tomcat、nginx、RabbitMQ、Redis，ElasticSearch

配置代理 一、永久设置 //编辑配置文件 vi /etc/profile //在该配置文件的最后添加代理配置 export http_proxyhttp://f1336515:password10.137.255.169:3128 //代理服务器ip地址和端口号 export https_proxyhttp://f1336515:password10.137.255.169:3128 //代理服务器ip…
阅读更多...
【软考网络管理员】2023年软考网管初级常见知识考点（11）-TCP和UDP详解

【软考网络管理员】2023年软考网管初级常见知识考点（11）-TCP和UDP详解

涉及知识点 传输控制协议TCP是什么&#xff0c;三次握手的概念理解&#xff0c;用户数据报协议UDP是什么&#xff0c;软考网络管理员常考知识点&#xff0c;软考网络管理员网络安全&#xff0c;网络管理员考点汇总。 原创于&#xff1a;CSDN博主-《拄杖盲学轻声码》&#xff0…
阅读更多...
AntV G6新版源码浅析

AntV G6新版源码浅析

前言 AntV是蚂蚁金服全新一代数据可视化解决方案&#xff0c;其中G6主要用于解决图可视领域相关的前端可视化问题&#xff0c;其是一个简单、易用、完备的图可视化引擎。本文旨在通过简要分析G6 5.x版本源码来对图可视领域的一些底层引擎进行一个大致了解&#xff0c;同时也为…
阅读更多...
【玩转Linux操作】详细讲解expr,read,echo,printf,test,[]等命令

【玩转Linux操作】详细讲解expr,read,echo,printf,test,[]等命令

&#x1f38a;专栏【玩转Linux操作】 &#x1f354;喜欢的诗句&#xff1a;更喜岷山千里雪 三军过后尽开颜。 &#x1f386;音乐分享【free loop】 大一同学小吉&#xff0c;欢迎并且感谢大家指出我的问题&#x1f970; 文章目录 &#x1f354;expr命令⭐表达式说明 &#x1f3…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023