题目:
求出 0~100000 之间的所有 自幂数 并输出。
自幂数是指一个n位数,其各位数字的n次方之和恰好等于该数本身,
如:153=1^3+5^3+3^3,
则153是一个自幂数。
=========================================================================
思路:
总体思路:
(一).
计算 i 的位数:
使用 for循环 产生 0~100000 的数(变量i)
使用一个变量 tmp 代替 i ,防止后续操作改变循环变量 i:
int tmp = i;
开始计算 i 的位数:
一个数 至少也是 一位数,所以 n 起始为 1 :
n = 1;
使用 while循环,如果 tmp/10 不为0,说明有位数,位数加一,n+1,直到 tmp/10 == 0
(二).
求每一位的 n次方之和:
因为上一步 tmp /= 10 改变了 tmp 的值,所以要再替换一次 i :
tmp = i;
创建变量 sum 存放每位次方后的和:
int sum = 0;
使用 while循环,如果 tmp 不等于 0 就继续取出当前位进行计算:
sum += pow(tmp % 10, n);
pow()函数为求第一个参数的第二个参数次方,需要<math.h>头文件
%10 取出当前位后,求出当前位的n次方,再求和赋给sum
计算完当前位后,移至该数的下一位:
tmp /= 10;
(三).
判断 sum 是不是自幂数,是则进行打印
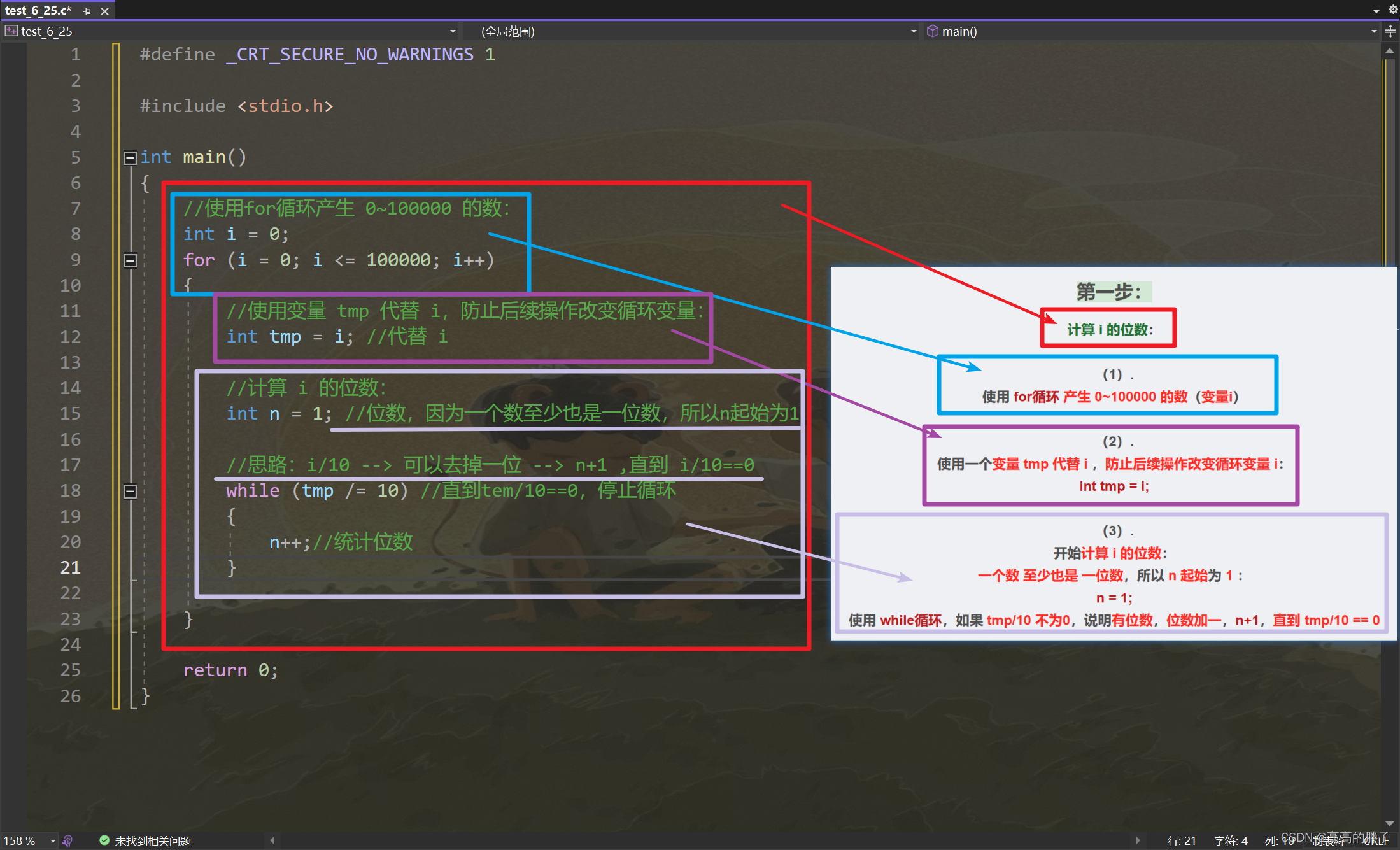
第一步:
计算 i 的位数:
(1).
使用 for循环 产生 0~100000 的数(变量i)
(2).
使用一个变量 tmp 代替 i ,防止后续操作改变循环变量 i:
int tmp = i;
(3).
开始计算 i 的位数:
一个数 至少也是 一位数,所以 n 起始为 1 :
n = 1;
使用 while循环,如果 tmp/10 不为0,说明有位数,位数加一,n+1,直到 tmp/10 == 0
实现代码:
#include <stdio.h> int main() { //使用for循环产生 0~100000 的数: int i = 0; for (i = 0; i <= 100000; i++) { //使用变量 tmp 代替 i,防止后续操作改变循环变量: int tmp = i; //代替 i //计算 i 的位数: int n = 1; //位数,因为一个数至少也是一位数,所以n起始为1 //思路:i/10 --> 可以去掉一位 --> n+1 ,直到 i/10==0 while (tmp /= 10) //直到tem/10==0,停止循环 { n++;//统计位数 } } return 0; }实现图片:
第二步:
求每一位的 n次方之和:
(1).
因为上一步 tmp /= 10 改变了 tmp 的值,所以要再替换一次 i :
tmp = i;
(2).
创建变量 sum 存放每位次方后的和:
int sum = 0;
(3).
使用 while循环,如果 tmp 不等于 0 就继续取出当前位进行计算:
sum += pow(tmp % 10, n);
pow()函数为求第一个参数的第二个参数次方,需要<math.h>头文件
%10 取出当前位后,求出当前位的n次方,再求和赋给sum
计算完当前位后,移至该数的下一位:
tmp /= 10;
实现代码:
#include <stdio.h> #include <math.h> int main() { //使用for循环产生 0~100000 的数: int i = 0; for (i = 0; i <= 100000; i++) { //使用变量 tmp 代替 i,防止后续操作改变循环变量: int tmp = i; //代替 i //计算 i 的位数: int n = 1; //位数,因为一个数至少也是一位数,所以n起始为1 //思路:i/10 --> 可以去掉一位 --> n+1 ,直到 i/10==0 while (tmp /= 10) //直到tem/10==0,停止循环 { n++;//统计位数 } //因为上面改变了 tmp /= 10 ,改变了 tmp 的值, //所以要再替换一次 i : tmp = i; //创建变量 sum 存放该数每一位次方的和: int sum = 0; //只要 i 不等于0,就继续取出下一位: while (tmp) { //%10,取出一位后,求出该位的n次方,再求和 sum += pow(tmp % 10, n); //计算下一位: tmp /= 10; } } return 0; }实现图片:
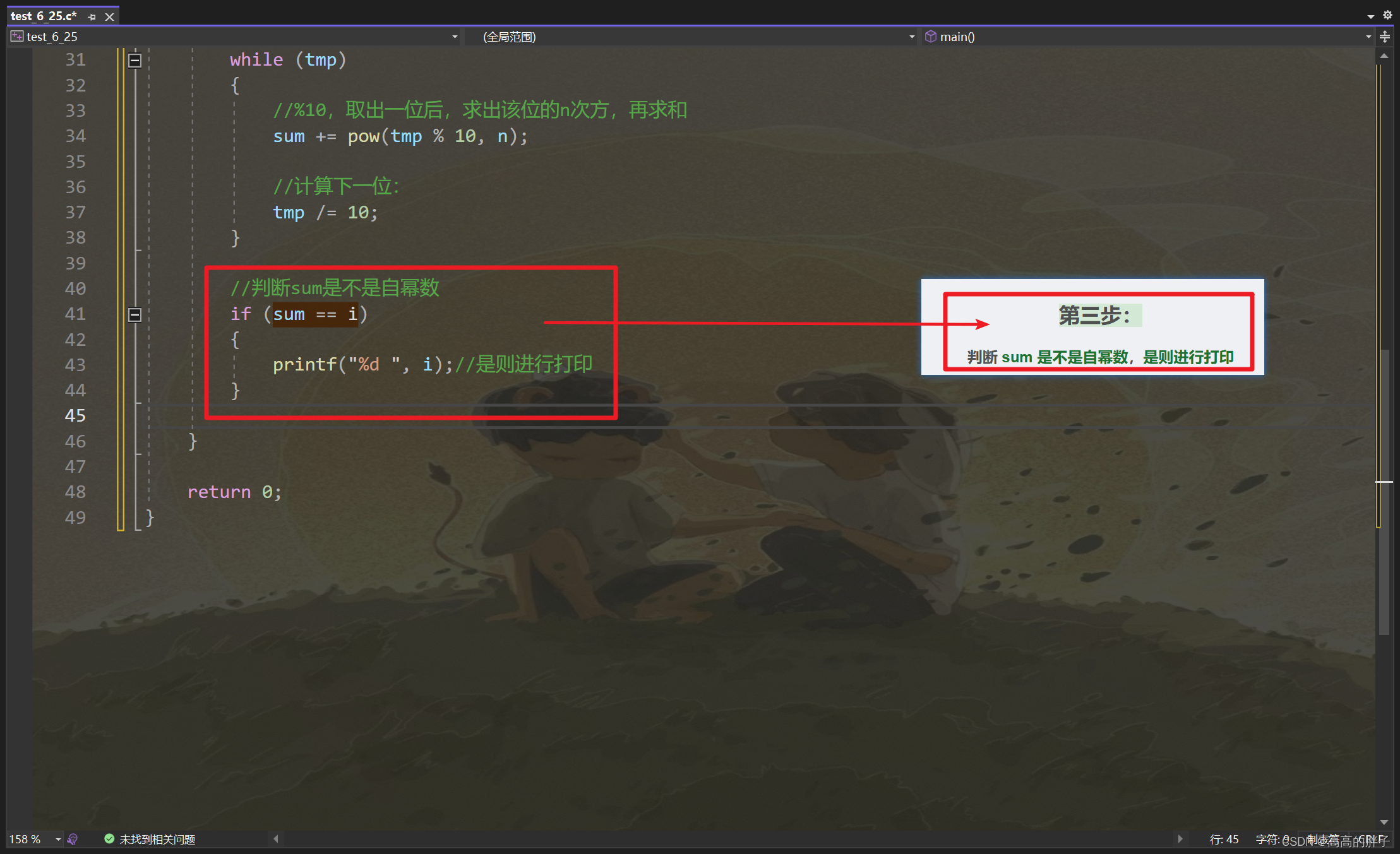
第三步:
判断 sum 是不是自幂数,是则进行打印
实现代码:
#include <stdio.h> #include <math.h> int main() { //使用for循环产生 0~100000 的数: int i = 0; for (i = 0; i <= 100000; i++) { //使用变量 tmp 代替 i,防止后续操作改变循环变量: int tmp = i; //代替 i //计算 i 的位数: int n = 1; //位数,因为一个数至少也是一位数,所以n起始为1 //思路:i/10 --> 可以去掉一位 --> n+1 ,直到 i/10==0 while (tmp /= 10) //直到tem/10==0,停止循环 { n++;//统计位数 } //因为上面改变了 tmp /= 10 ,改变了 tmp 的值, //所以要再替换一次 i : tmp = i; //创建变量 sum 存放该数每一位次方的和: int sum = 0; //只要 i 不等于0,就继续取出下一位: while (tmp) { //%10,取出一位后,求出该位的n次方,再求和 sum += pow(tmp % 10, n); //计算下一位: tmp /= 10; } //判断sum是不是自幂数 if (sum == i) { printf("%d ", i);//是则进行打印 } } return 0; }实现图片:
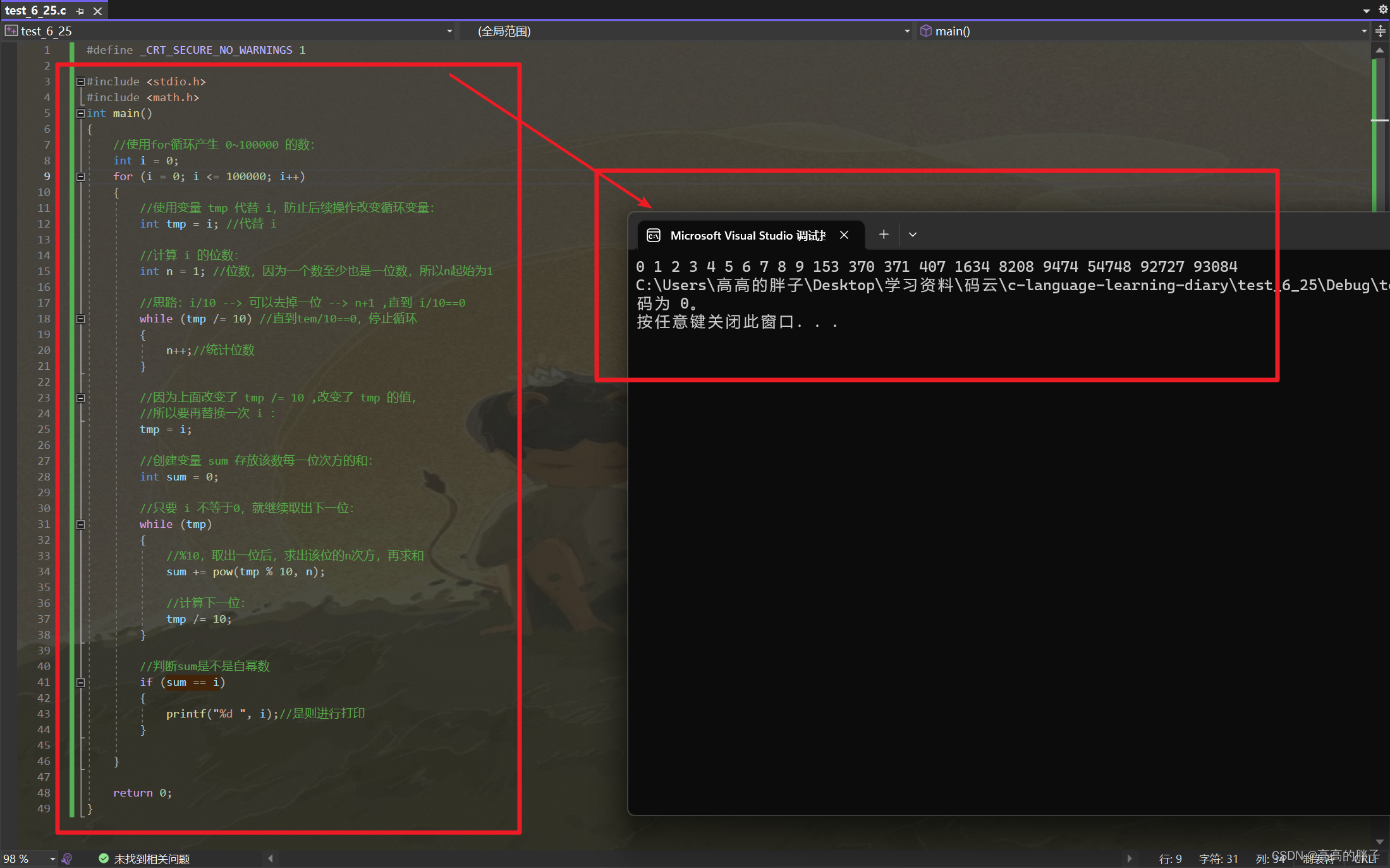
最终代码和实现效果
最终代码:
#include <stdio.h> #include <math.h> int main() { //使用for循环产生 0~100000 的数: int i = 0; for (i = 0; i <= 100000; i++) { //使用变量 tmp 代替 i,防止后续操作改变循环变量: int tmp = i; //代替 i //计算 i 的位数: int n = 1; //位数,因为一个数至少也是一位数,所以n起始为1 //思路:i/10 --> 可以去掉一位 --> n+1 ,直到 i/10==0 while (tmp /= 10) //直到tem/10==0,停止循环 { n++;//统计位数 } //因为上面改变了 tmp /= 10 ,改变了 tmp 的值, //所以要再替换一次 i : tmp = i; //创建变量 sum 存放该数每一位次方的和: int sum = 0; //只要 i 不等于0,就继续取出下一位: while (tmp) { //%10,取出一位后,求出该位的n次方,再求和 sum += pow(tmp % 10, n); //计算下一位: tmp /= 10; } //判断sum是不是自幂数 if (sum == i) { printf("%d ", i);//是则进行打印 } } return 0; }实现效果:





![【玩转Linux操作】详细讲解expr,read,echo,printf,test,[]等命令](https://img-blog.csdnimg.cn/435ac06145bc478ba4e7a7fa70623766.png)