动态规划

记住动归5部曲：
1.确定dp数组（dp table）以及下标的含义

2.确定递推公式

3.dp数组如何初始化

4.确定遍历顺序

5.举例推导dp数组

开撸——基础题目

1. lc509 斐波那契数

描述：

斐波那契数（通常用 F(n) 表示）形成的序列称为斐波那契数列。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。给定 n ，请计算 F(n) 。其中F(0) = 0，F(1) = 1

示例：

输入：n = 3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2

Solution：
按照以前的写法，直接递归就完事了，但是这样算法复杂度肯定高。注意到其实在整个递归过程有重复计算的；

比如F（6）= F(5）+F（4），然后分别计算F（5）和F（4），但是计算F（5）时还会遇到计算F（4），但此时他们俩已经彼此分开了。

其实这就是我们说的某一问题有很多重叠子问题

public int fib(int n) {
        if(n<=1)
        return n;
        // 1.dp数组的含义：第i个数的斐波那契数值是dp[i]
        int[] dp = new int[n+1];
        
        // 2. 递推公式
        // dp[i]=dp[i-1]+dp[i-2];

        // 3.初始化
        dp[0]=0;
        dp[1]=1;
        
        // 4.遍历顺序
        for(int i=2;i<n+1;i++)
        {
            dp[i]=dp[i-1]+dp[i-2];
        }
        return dp[n];
    }

2. lc746 使用最小花费爬楼梯

描述：

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。请你计算并返回达到楼梯顶部的最低花费。

示例：

输入：cost = [1,100,1,1,1,100,1,1,100,1]
输出：6

Solution：

 public int minCostClimbingStairs(int[] cost) {
        int len = cost.length;
        // 1.dp数组含义：到达第i台阶所花费的最少体力为dp[i]

        // 2.递推公式
        // dp[i] = Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
         
        int[] dp = new int[len+1];
        // 3. 初始化
        dp[0] = 0;
        dp[1] = 0;
        // 4. 遍历
        for(int i=2;i<=len;i++)
        {
            dp[i] = Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
        }
        return dp[len];
    }

3. lc63 不同路径II

描述：

一个机器人每次只能向下或者向右移动一步，试图达到网格的右下角，现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？网格中的障碍物和空位置分别用 1 和 0 来表示

示例：

输入：obstacleGrid = [ [0,0,0],[0,1,0],[0,0,0] ]
输出：2

Solution：
相比较62题多了个“障碍”

 public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;

        int[][] dp = new int[m][n];

         //如果在起点或终点出现了障碍，直接返回0
        if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) {
            return 0;
        }

        for(int i=0;i<m && obstacleGrid[i][0]==0;i++)
        {
            dp[i][0]=1;
        }

        for(int i=0;i<n && obstacleGrid[0][i]==0;i++)
        {
            dp[0][i]=1;
        }
        

        for(int i=1;i<m;i++)
        {
            for(int j=1;j<n;j++)
            {
                if(obstacleGrid[i][j]==1)
                dp[i][j]=0;
                else
                dp[i][j] = dp[i][j-1]+dp[i-1][j];
            }
        }
        return dp[m-1][n-1];
    }

4. lc343 整数拆分

lc343 链接

描述：

给定一个正整数 n ，将其拆分为 k 个正整数的和（ k >= 2 ），并使这些整数的乘积最大化。返回你可以获得的最大乘积

示例：

输入：输入: n = 10
输出: 36 （10 = 3 + 3 + 4, 3 × 3 × 4 = 36）

Solution：
注意看递推公式：
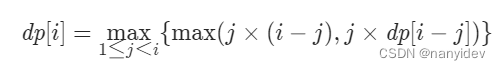
在这里插入图片描述

public int integerBreak(int n) {
        int[] dp = new int[n+1];

        if(n==2)
           dp[n]=1;
   
        for(int i=3;i<=n;i++)
        {
            int curMax=0;
            for(int j=1;j<i;j++)
            {
                curMax = Math.max(curMax,Math.max(j*(i-j),j*dp[i-j]));
            }
            dp[i] = curMax;
        }

        return dp[n];
    }