目录
LDA降维
思想
matlab代码
fisherface
思想
matlab代码
人脸识别
思想
matlab代码
LDA降维
思想
首先,代码通过使用dir函数获取指定路径下所有以".bmp"结尾的文件,并存储在变量pictures中。
然后,定义了一些参数:people表示人数,personPictureNumber表示每个人的图像数量,Dimension表示图像的维度大小,pictureNumber表示总图像数量。
接下来,创建一个空矩阵sample,用于存储所有图像的向量表示。然后利用循环遍历每个图片,并将其读取、转换为双精度类型,并将其转换为列向量picture。最后将该列向量添加到sample矩阵中。
接下来是LDA部分的代码。首先定义了两个空的矩阵Sb和Sw,分别表示类间散度矩阵和类内散度矩阵。然后,通过循环遍历每个人的图像,计算出每个人图像的均值向量,并计算出类间散度矩阵Sb。同时,将每个人图像的均值向量存储在meanPerson中。接下来,计算类内散度矩阵Sw,循环遍历每个图像,计算出每个图像与其对应人的均值向量之差,并计算出类内散度矩阵Sw。
然后根据不同模型进行不同处理构建协方差矩阵,然后提取特征向量。
matlab代码
pictures=dir('C:\Users\Yezi\Desktop\机器学习\face10080\*.bmp');
people=15;
personPictureNumber=11;
Dimension=100*80;
pictureNumber=people*personPictureNumber;
sample=[];
for i=1:pictureNumber
picture=imread("C:\Users\Yezi\Desktop\机器学习\face10080\"+pictures(i).name);
picture=double(picture);
picture=picture(:);
sample=[sample,picture];
end
% LDA
meanPerson=[];
meanTotal=mean(sample,2);
Sb=zeros(Dimension,Dimension);
for i=0:people-1
temp=sample(:,i*personPictureNumber+1:(i+1)*personPictureNumber);
one=mean(temp,2)-meanTotal;
Sb=Sb+one*one';
meanPerson=[meanPerson,mean(temp,2)];
end
Sb=Sb/people;
Sw=zeros(Dimension,Dimension);
for i=1:pictureNumber
one=sample(:,i)-meanPerson(floor((i-1)/personPictureNumber)+1);
Sw=Sw+one*one';
end
Sw=Sw/pictureNumber;
% 经典
covMatrix=pinv(Sw)*Sb;
% 正则
% Sb=Sb+eye(Dimension)*10^-6;
% covMatrix=pinv(Sw)*Sb;
% 减法
% covMatrix=Sb-Sw;
[egienvectors,diagonalMatrix]=eig(covMatrix);
egienvalues=diag(diagonalMatrix);
[egienvalues,order]=sort(egienvalues,'descend');
egienvectors=egienvectors(:,order);fisherface
思想

首先,将样本矩阵sample中的第一列取出,表示选择了一个人脸图像作为重建的源图像,存储在变量oneFace中。
然后,通过循环遍历特征维度,从1到8逐渐增加。在每个循环中,选取特征向量矩阵egienvectors中的前dimension列,表示选择了部分特征向量用于重建。这些特征向量被存储在变量egienvector中。
接下来,通过将特征向量矩阵egienvector与其转置的乘积与源图像oneFace相乘,得到重建的人脸图像rebuildFace。然后,通过reshape函数将rebuildFace重新变换回100x80的图像矩阵。
然后,使用subplot函数将多个子图排列在一个2x4的网格上,其中每个子图显示一个特征维度下的重建人脸图像。imshow函数显示重建的人脸图像,并使用mat2gray函数将图像数据转换为灰度范围[0,1]内的值。xlabel函数设置子图的标题,显示当前特征维度。
通过以上的循环和绘图操作,代码可以展示在不同的特征维度下,对原始人脸图像的重建效果。随着特征维度的增加,重建图像将逐渐接近源图像,并展示出更多的细节和结构信息。
matlab代码
oneFace=sample(:,1);
for dimension=1:1:8
egienvector=egienvectors(:,1:dimension);
rebuildFace=egienvector*(egienvector'*oneFace);
rebuildFace=reshape(rebuildFace,100,80);
subplot(2,4,dimension);
imshow(mat2gray(rebuildFace));
xlabel(sprintf("dimension=%d",dimension));
end人脸识别
思想
首先,定义训练样本数trainNumber和测试样本数testNumber,并创建了空的训练数据矩阵trainData和测试数据矩阵testData。
然后,通过两个循环将样本矩阵sample中的数据按照一定规则划分为训练数据和测试数据。第一个循环根据不同的人数进行迭代,并将每个人的前trainNumber个图像添加到trainData中。第二个循环同样根据不同的人数进行迭代,并将每个人的后面的testNumber个图像添加到testData中。
接下来,定义了空的结果矩阵result,用于存储不同特征维度下的分类准确率。
然后,通过两个嵌套循环遍历K近邻算法的参数:knnK和dimension。在每个循环中,选择特征向量矩阵egienvectors中的前dimension列,表示选择了部分特征向量进行降维。这些特征向量被存储在变量egienvector中。
接下来,通过矩阵乘法运算将训练数据和测试数据投影到特征向量所构成的子空间中,得到降维后的训练数据trainDataTemp和测试数据testDataTemp。
然后,定义了变量error用于记录分类错误的样本数量。通过计算测试数据的数量和训练数据的数量,进行两个嵌套循环遍历测试数据。在每个测试样本中,计算与所有训练样本之间的欧式距离,并对距离进行排序。然后,根据K近邻算法的思想,选择距离最近的knnK个训练样本作为邻居。
接下来,根据邻居的类别信息,判断测试样本的类别。如果邻居中只有一个类别出现次数最多,则将该类别作为测试样本的预测类别;否则,使用出现次数最多的类别作为预测类别。
最后,统计错误分类的样本数量,并计算分类准确率。将准确率存储在结果矩阵result中。
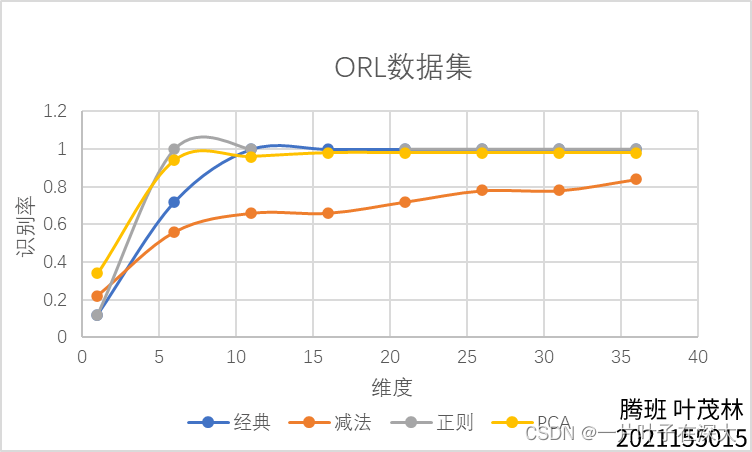
最后,通过调用plot函数,将特征维度dimension作为横轴,分类准确率result作为纵轴进行绘图,展示不同特征维度下的分类准确率曲线。
matlab代码
trainNumber=4;
testNumber=3;
trainData=[];
testData=[];
for i=0:people-1
trainData=[trainData,sample(:,i*personPictureNumber+1:i*personPictureNumber+trainNumber)];
end
for i=0:people-1
testData=[testData,sample(:,i*personPictureNumber+trainNumber+1:i*personPictureNumber+personPictureNumber)];
end
result=[];
for knnK=1:1
for dimension=1:1:10
egienvector=egienvectors(:,1:dimension);
trainDataTemp=egienvector'*trainData;
testDataTemp=egienvector'*testData;
error=0;
testDataNumber=size(testDataTemp,2);
trainDataNumber=size(trainDataTemp,2);
for i=1:testDataNumber
distances=[];
for j=1:trainDataNumber
distance=0;
for k=1:dimension
distance=distance+(testDataTemp(k,i)-trainDataTemp(k,j))^2;
end
distances=[distances,distance];
end
[distances,index]=sort(distances);
rightIndex=floor((i-1)/testNumber)+1;
testIndex=0;
knn=[];
for k=1:knnK
knn=[knn,floor((index(k)-1)/trainNumber)+1];
end
[modeIndex,times]=mode(knn);
if times==1
testIndex=knn(1);
else
testIndex=modeIndex;
end
if testIndex~=rightIndex
error=error+1;
end
end
rate=(testDataNumber-error)/testDataNumber;
result=[result,rate];
end
end
X=1:1:10;
plot(X,result);