DAY29：回溯算法（四）组合总和+组合总和Ⅱ

文章目录

- 39.组合总和
- - 思路
  - 伪代码
  - - 为什么传入i而不是i+1，不会导致无限循环
  - 完整版
  - 剪枝优化
  - 剪枝修改完整版
  - - 补充：std::sort升降序的问题（默认升序）
- 40.组合总和Ⅱ
- - 思路
  - 最开始的写法
  - debug测试：逻辑错误
  - 修改完整版：去重
  - - used数组的作用，为什么不能删掉
  - debug测试：
  - - 1. Char 9: runtime error: reference binding to null pointer of type 'int' (stl_vector.h)
    - 2. Line 1034: Char 34: runtime error: addition of unsigned offset to 0x603000000070 overflowed to 0x60300000006c (stl_vector.h)
  - 总结
  - - vector的动态特性补充

39.组合总和

因为本题没有组合数量要求，仅仅是总和的限制，所以递归没有层数的限制，只要选取的元素总和超过target，就返回！

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的所有不同组合，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates = [2], target = 1
输出: []

提示：

1 <= candidates.length <= 30
2 <= candidates[i] <= 40
candidates 的所有元素互不相同
1 <= target <= 40

思路

本题没有重复元素，所以暂且不涉及去重问题。

与组合的一个很大区别就是，本题没有涉及到k，也就是没有规定一定要K个元素总和为target。而本题没有限制K，是靠目标和sum的值来控制树的深度。

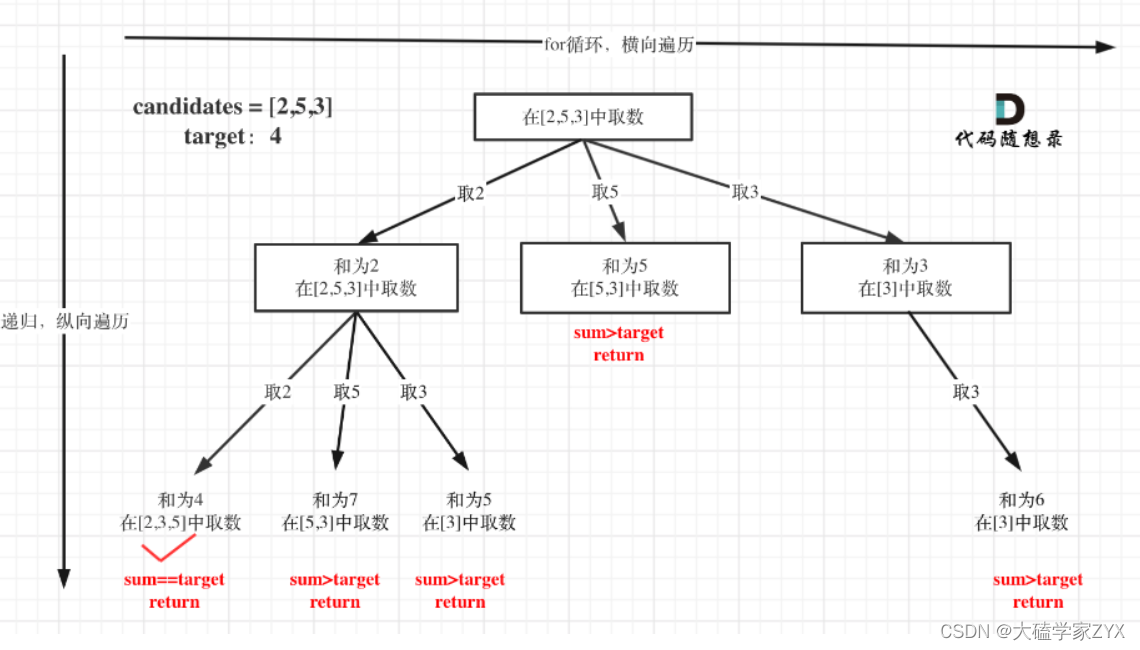
另外，题目中说candidates 中的 同一个 数字可以 无限制重复被选取 ，这也就是说，组合里可以存在重复的元素！也就是说绘制树形结构的时候，剩下的元素不能去掉当前元素本身。树形图示例如下：

在这里插入图片描述
这里有一个问题，因为元素本身被选取的次数是不限制的，一共选取的元素个数也是不限制的，那么应该如何限制本身被选了多少次呢？因为自身如果一直被选择下去，就会死循环了，唯一的限制就是和targetSum这个值。

因为1 <= candidates[i] <= 200，所以说并不存在出现0的情况，也就是说我们可以根据这条分支的sum值大于target数值，直接进行return遍历下一个分支！也就是下图中粉色线条删除的部分，后面一定是在这个分支上继续累加，因为没有0和负数，所以sum只会越来越大。

在这里插入图片描述

伪代码

组合问题基本都是定义一个一维组合数组，一个二维结果数组
因为本题是组合问题而不是子集问题，本题是从一个集合里面搜索符合条件的所有组合，因此需要startIndex来控制搜索的起点！
如果已经大于了，就没有必要再往组合里面添加元素了！应该直接return，return了就可以进行元素修改了！
元素本身在组合里可重复选择，区别就在于startIndex这里，下层依然是i开始，而不是i+1。注意startIndex只是个参数，参数是根据i来改变的！

void backtracking(vector<vector<int>>&result,vector<int>&path,vector<int>&candidates,int target,int sum,int startIndex){
    //终止条件，这里不能只写if(sum==target)，因为本题没有K的限制，如果一直没有，会一直搜索下去！
    //如果大于，后面就没必要再添加元素了，应该进行修改元素
    if(sum>target){
        return;
    }
    if(sum==target){
        result.push_back(path);
        return;
    }
    //单层搜索
    for(int i=startIndex;i<candidate.size();i++){
        sum += candidates[i];
        path.push_back(candidates[i]);
        //本身可重复，区别就在递归传入startIndex参数这里！这里下层依然是i开始，而不是i+1!
        backtracking(result,path,candidates,target,sum,i);
        //回溯
        sum -= candidates[i];
        path.pop_back();
    }
    
}

为什么传入i而不是i+1，不会导致无限循环

因为递归的时候，我们传入的循环开始参数是i而不是i+1，因此会考虑到递归能不能进行下去，会不会导致无限循环的问题。

backtracking(result,path,candidates,target,sum,i);

当我们传递i作为startIndex，我们允许下一次递归从相同的位置开始，从而包含当前正在处理的元素。因此，如果当前元素可以被多次选择以达到目标值，那么这种情况也会被考虑到。如果我们传递i+1作为startIndex，那么下一次递归将会跳过当前元素，不再考虑重复选择当前元素的情况。

然而，我们需要注意的是，这个递归算法并不会陷入无限循环，因为我们有两个明确的终止条件：当我们的总和超过目标值或者等于目标值时，我们将停止递归。例如下图的情况：
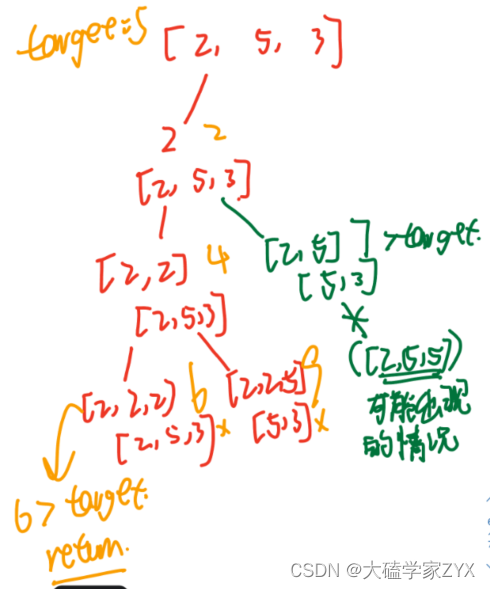
在这里插入图片描述

另外，另一个误区是，尽管我们在递归调用中传递了i（这意味着我们可能会多次选择同一个元素），但这并不会阻止递归进行下去。因为在for循环中，for循环会在pop本层不符合条件的i之后，继续尝试i+1的选项。

在这个回溯算法中，我们是在**for循环中遍历candidates数组的每一个元素。当我们在一次递归调用中传递了i而不是i+1，我们实际上仅仅是在允许算法选择当前的元素candidates[i]多次**。然而，这并不会阻止大的for循环在后续的迭代中尝试其他的元素。

完整版

class Solution {
public:
    void backtracking(vector<int>&path,vector<vector<int>>&result,vector<int>& candidates, int target,int sum,int startIndex){
        //终止条件
        if(sum>target){
            return;
        }
        if(sum==target){
            result.push_back(path);
            return;
        }
        //单层搜索
        for(int i=startIndex;i<candidates.size();i++){
            sum += candidates[i];
            path.push_back(candidates[i]);
            //递归,注意本身元素可重复，应当传入i而不是i+1！
            backtracking(path,result,candidates,target,sum,i);
            sum -= candidates[i];
            path.pop_back();
        }
    }
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector<int>path;
        vector<vector<int>>result;
        int sum=0;
        int startIndex=0;
        backtracking(path,result,candidates,target,sum,startIndex);
        return result;
    }
};

剪枝优化

我们先看一下代码随想录里完整的树形结构：
在这里插入图片描述
组合问题的剪枝基本都是在for循环的搜索范围上做文章。

本题的剪枝操作是对candidates数组进行排序操作，如果前面的分支，例如[2,3]结果已经大于目标值，后面的[2,5]就没必要再搜索了！

也就是说，对总集合排序之后，如果下一层的sum（就是本层的 sum + candidates[i]）已经大于target，就可以结束本轮for循环的遍历。

如图：

在这里插入图片描述
for循环剪枝代码：

for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++){}

剪枝重点就是当前遍历的candidates[i]+sum>target的时候，后面可以直接全部剪掉！

剪枝修改完整版

class Solution {
public:
    void backtracking(vector<int>&path,vector<vector<int>>&result,vector<int>& candidates, int target,int sum,int startIndex){
        //终止条件
        if(sum>target){
            return;
        }
        if(sum==target){
            result.push_back(path);
            return;
        }
        //单层搜索
        for(int i=startIndex;i<candidates.size()&&candidates[i]+sum<=target;i++){
            sum += candidates[i];
            path.push_back(candidates[i]);
            //递归,注意本身元素可重复，应当传入i而不是i+1！
            backtracking(path,result,candidates,target,sum,i);
            sum -= candidates[i];
            path.pop_back();
        }
    }
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector<int>path;
        vector<vector<int>>result;
        int sum=0;
        int startIndex=0;
        //直接库函数排序，sort默认从小到大
        sort(candidates.begin(),candidates.end());
        //传入排序好的
        backtracking(path,result,candidates,target,sum,startIndex);
        return result;
    }
};

补充：std::sort升降序的问题（默认升序）

注意，在C++中，std::sort函数默认的排序方式是从小到大，也就是升序排序。这个函数会对输入范围内的元素进行排序，使得排序后的元素序列是非递减的。

如果要实现降序排序，你可以给std::sort函数提供第三个参数，即一个自定义的比较函数或者lambda表达式。这个比较函数定义了两个元素的比较规则。

例如，如果想对candidates数组进行降序排序，你可以这样做：

std::sort(candidates.begin(), candidates.end(), std::greater<int>());

在这个代码中，std::greater<int>()是一个函数对象，它定义了一个规则，使得sort函数会按照这个规则进行排序，也就是降序排序。

另一种方式是使用lambda表达式来定义比较规则：

std::sort(candidates.begin(), candidates.end(), [](int a, int b) {return a > b;});

在这个代码中，[](int a, int b) {return a > b;}是一个lambda表达式，它接受两个参数a和b，如果a > b，则返回true，这样sort函数就会按照这个规则进行降序排序。

40.组合总和Ⅱ

本题最重要的一点是去重！并且本题只有树层去重，树枝不能去重，此时要靠单独的次数统计数组来防止树枝也被去重
防止访问vector数组下标-1越界，涉及到下标-1运算的都必须检查越界问题

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

注意：解集不能包含重复的组合。

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

示例 2:

输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]

提示:

1 <= candidates.length <= 100
1 <= candidates[i] <= 50
1 <= target <= 30

思路

这道题和组合总和区别就在于：

不包含本身。因为题目写的是candidates 中的每个数字在每个组合中只能使用一次。
candidates是有重复的！因此不能直接简单的把组合的写法改为递归i+1，还要进行去重操作！否则输出结果会出现一模一样元素的组合（详见debug测试），因为candidates后面还有和前面重复的元素！
用map或者set去重很容易超时，所以需要搜索的过程中就进行去重！

同时，题目中说，candidates` 中的每个数字在每个组合中只能使用一次。这里很容易理解错误，实际上，candidates集合中本来就重复的元素，只需要在树层里去重，树枝并不需要去重。可以看示例1的输出，包含了[1,1,6]，说明本题是按照candidates前后两个1不一样来算的。

树层去重和树枝去重如下图所示。

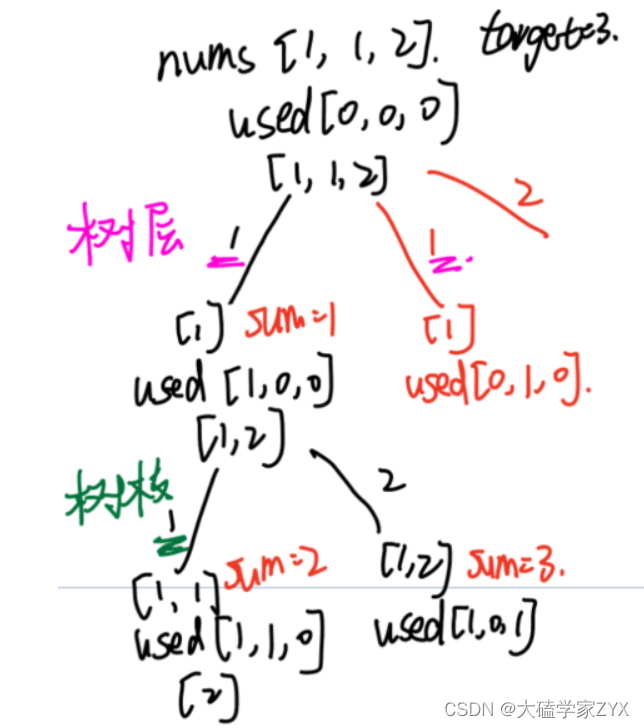
在这里插入图片描述
类似上图，由于第一个1往后会取到所有的数字，所以第二个1往后取，一定会和第一个1发生重复。

但是树枝上有重复，是允许的，因为示例有组合出现数值相同的元素的例子。

最开始的写法

class Solution {
public:
    void backtracking(vector<int>&path,vector<vector<int>>&result,vector<int>& candidates,int sum,int target,int startIndex){
        //终止条件
        if(sum>target){
            return;
        }
        if(sum==target){
            result.push_back(path);
            return;
        }
        //单层搜素
        for(int i=startIndex;i<candidates.size();i++){
            sum += candidates[i];
            path.push_back(candidates[i]);
            backtracking(path,result,candidates,sum,target,i+1);
            sum -= candidates[i];
            path.pop_back();
        }
    }
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
		vector<int>path;
        vector<vector<int>>result;
        int sum=0;
        int startIndex=0;
        backtracking(path,result,candidates,sum,target,startIndex);
        return result;
    }
};

debug测试：逻辑错误

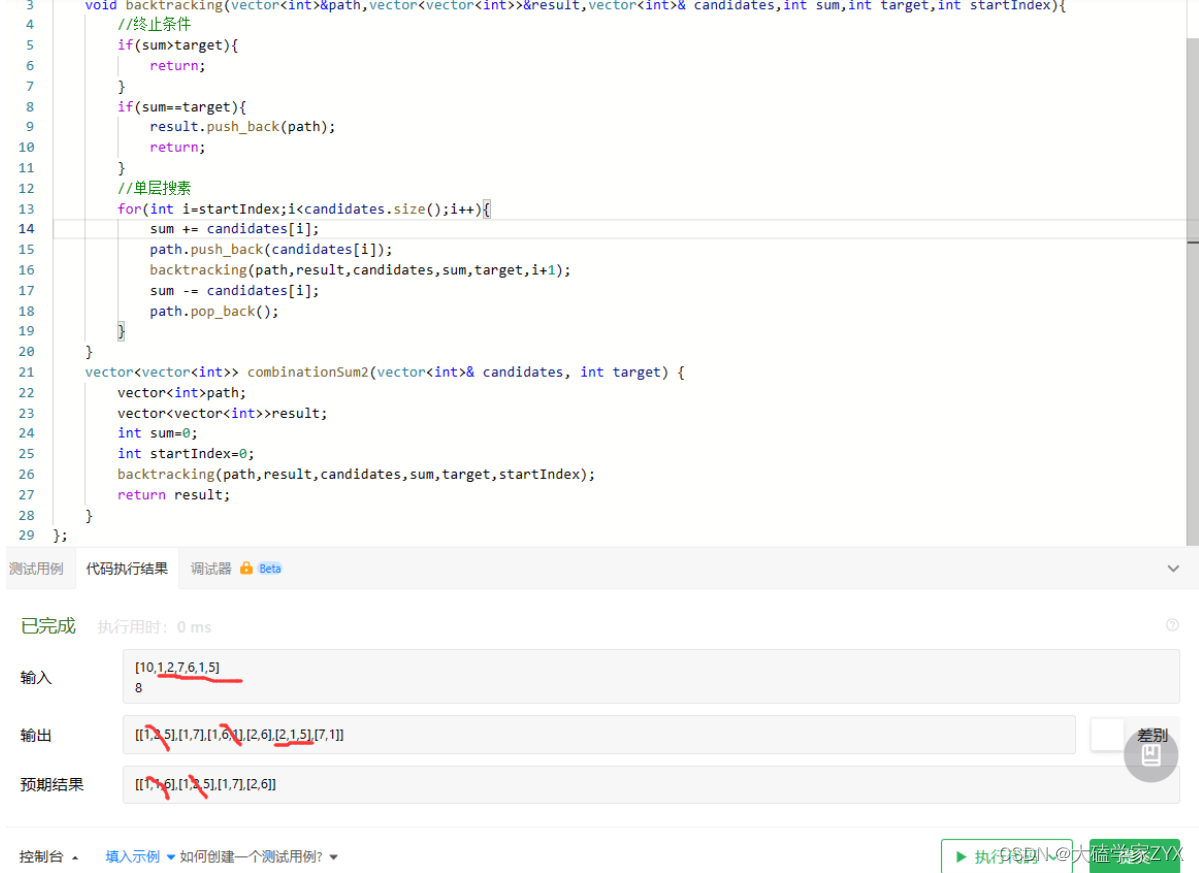
在这里插入图片描述
仔细看一下输入，发现本题的candidates是有重复的！也就是说candidates里面，备选集合会有重复，但是结果不能有重复。

用map或者set去重很容易超时，所以需要搜索的过程中就进行去重！

修改完整版：去重

去重需要传入一个used数组，来统计哪些元素被使用过。used数组的目的就是为了区分是树层还是树枝。
去重之前要做一个排序，使得重复的元素都放在一起，方便去重的时候进行判断！
防止访问数组下标-1越界，涉及到下标-1运算的都必须检查越界问题

class Solution {
public:
    void backtracking(vector<int>&path,vector<vector<int>>&result,vector<int>& candidates,int sum,int target,vector<int>&used,int startIndex){
        //终止条件
        if(sum>target){
            return;
        }
        if(sum==target){
            result.push_back(path);
            return;
        }
        //单层搜索
        for(int i=startIndex;i<candidates.size();i++){
            //防止访问下标-1越界，涉及到下标-1的都必须检查越界问题
            if(i>=1&&candidates[i]==candidates[i-1]&&used[i-1]==0){
                continue; //直接不处理，跳到for循环的下一个
            }
            sum += candidates[i];
            path.push_back(candidates[i]);
            //记录use过当前的i
            used[i]=1;
            //开始递归
            backtracking(path,result,candidates,sum,target,used,i+1);
            //回溯，重置use
            sum -= candidates[i];
            path.pop_back();
            used[i]=0;
        }
    }
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
		vector<int>path;
        vector<vector<int>>result;
        //注意这种带有初始大小和初始值的vector数组定义方式！需要访问used下标所以必须初始化
        vector<int>used(candidates.size(),0);
        int sum=0;
        int startIndex=0;
        sort(candidates.begin(),candidates.end());
        backtracking(path,result,candidates,sum,target,used,startIndex);
        return result;
    }
};

used数组的作用，为什么不能删掉

used数组的作用就是用来区分上层的树层和树枝的。本题树层必须去重，而树枝不能去重。

去重的逻辑：

if(candidates[i]==candidates[i-1]&&used[i-1]==0){
     //判断出i-1的used下标是0，也就是i-1并没有使用过，是树层而不是树枝！  
    continue;
}

我们继续以原数组[1,1,2]作为例子。

如果used[i-1]不为0，而是1的话，也就可能会是下图黄色笔标出的的情况：

在树枝里，递归到[1,1]这一层的时候，第二个1也满足candidates[i]==candidates[i-1]，如果不用used，递归到下层开始把下层的i加入path的时候。第二个1的分支就会直接continue被跳过，相当于整个[1,1]这一个分支都被剪掉了！此时会直接开始[1,2]这个分支，而原本的[1,1]分支作为树枝其实是被允许的，这个分支里的答案就漏掉了。

本质上，也就是每一层递归，i都是那一层树对应的值！

在这里插入图片描述
use需要重置的原因，本质上也是因为回溯回去的时候，需要把原来的元素拿出来，再放进去下一个元素。

debug测试：

1. Char 9: runtime error: reference binding to null pointer of type ‘int’ (stl_vector.h)

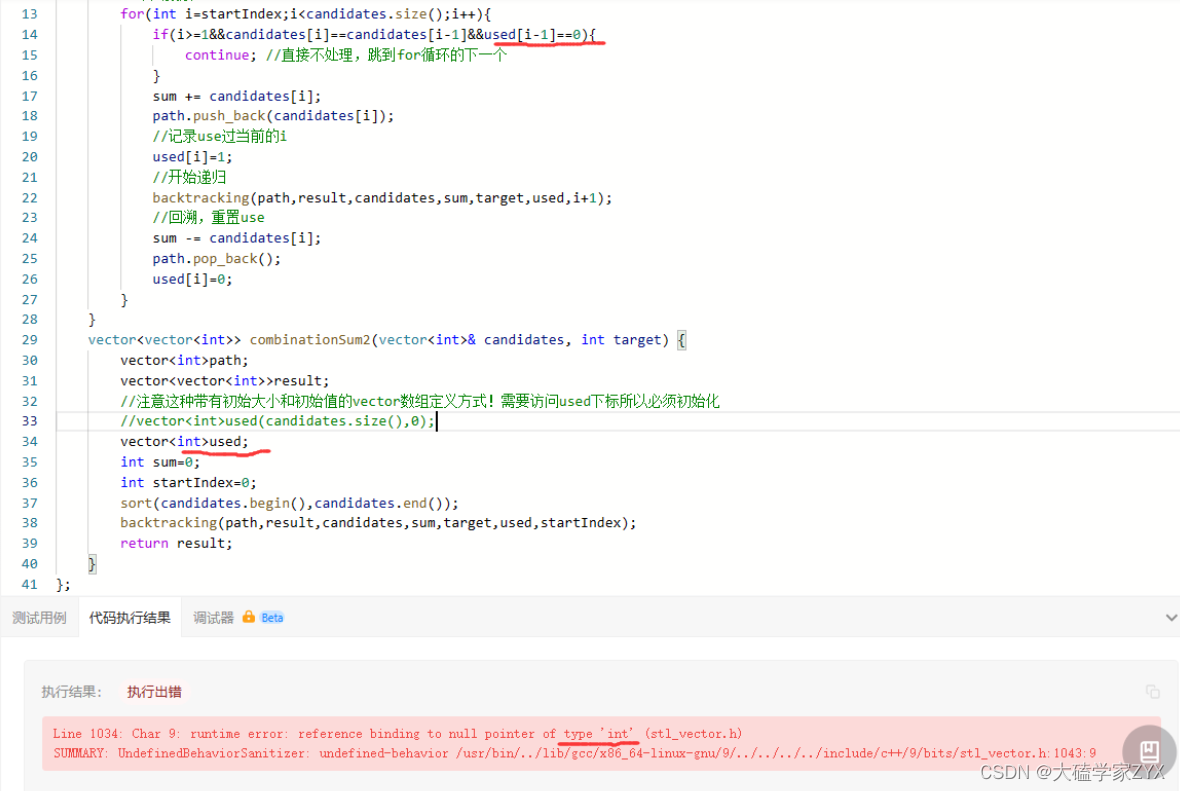
在这里插入图片描述
这个错误的发生是因为used没有初始化，而程序访问了used的下标。

“reference binding to null pointer of type ‘int’” 这个错误信息表示你试图访问一个int类型的空指针。在原版代码中，我们尝试在未初始化的used数组中使用下标操作符[]来访问或修改元素。int类型的空指针指的就是used数组为空。

used[i]=1和used[i]=0试图访问used的某个位置，但是由于used的大小为0，所以这将导致运行时错误。

应该在调用backtracking函数之前，将used的大小设置为candidates的大小，并将所有元素初始化为0。

vector<int>used(candidates.size(),0);

注意这种带有初始大小和初始值的vector数组定义方式！

2. Line 1034: Char 34: runtime error: addition of unsigned offset to 0x603000000070 overflowed to 0x60300000006c (stl_vector.h)

修改了used的初始化之后依旧报错，这个时候的问题出在i-1这里
在这里插入图片描述
当 i 等于0的时候，candidates[i-1]和used[i-1]会试图访问数组的负索引，这是未定义的行为，可能导致运行时错误。

你需要确保在进行这种操作之前检查 i 是否大于0：

if(i > 0 && candidates[i]==candidates[i-1]&&used[i-1]==0)

总结

上面这种报错：**Char 34: runtime error: addition of unsigned offset to 0x603000000070 overflowed to 0x60300000006c (stl_vector.h)**是因为数组下标越界，或者数组下标被访问的时候没有初始化造成的。

在大多数情况下，这种类型的错误信息表示尝试访问了数组的某个位置，而这个位置不在数组的有效范围内，也就是说，你的代码试图进行越界访问。当试图访问未初始化的数组元素或者超出数组范围的下标时，都可能发生这种错误。

具体来看

runtime error: addition of unsigned offset to 0x603000000070 overflowed to 0x60300000006c (stl_vector.h)

这是一个运行时错误，它表示在执行到stl_vector.h文件中的某一行时，发生了溢出。具体来说，这是一个无符号整数溢出错误，说明程序尝试将一个正值（无符号偏移）加到一个地址上，但结果却比原地址小，这表明发生了溢出。

一般情况下，这可能是由于在访问vector的元素时使用了负索引，而在C++中，vector的索引必须是非负的，所以导致了越界错误。尤其是在这个代码中，如果 i 为0，那么 candidates[i-1] 和 used[i-1] 就会尝试访问负索引，导致这个错误。所以必须在访问这些元素之前先检查 i 是否大于0。

而另一个报错Char 9: runtime error: reference binding to null pointer of type ‘int’ (stl_vector.h)，是因为试图访问一个int类型的空指针。

"int类型的空指针"是指在尝试访问或操作一个没有有效内存地址的 int 指针。这通常发生在试图访问或操作一个未初始化或者已经被销毁的指针。

vector的动态特性补充

std::vector 是一种动态数组，它只为它的元素分配内存。如果你没有给 std::vector 添加任何元素，或者你试图访问超出它当前大小的下标，就会访问到无效的内存地址，从而引发错误。这就是为什么需要在使用 std::vector<int> 的下标访问元素之前，先确保它有足够的空间，并初始化它的元素。