gcd 和 lcm

gcd 和 lcm 分别是最大公约数（Greatest common divisor）和最小公因数（Least Common Multiple）。

常用的 gcd 算法使用的是欧几里得算法，也就是辗转相除算法。原理如下：

1.有两个数a和b，我们把较大的数传给maxn,较小的数传给minx
2.用maxn对minx进行取余运算，如果余数为0，那么a,b的最大公约数为a,
3.若余数不为0，a,b的最大公约数为minx和余数的最大公约数，我们在循环到第一步进行计算。

将算法描述翻译成代码如下：

public int gcd(int a, int b) {
    if (a < b) return gcd(b, a);    // 确保 a 是较大的数字
    while (a % b != 0) {	// 一直相除到余数为 0
        int t = a % b;		// 求余数
        a = b;	// 
        b = t;	// 
    }
    return b;
}

推荐写法 ：
经过精简之后可以写成如下形式（原理是一样的，只不过从迭代改成了递归的形式，代码会更短一些。）（或者可以这样来理解这种写法基于的一个事实：对于任何两个整数a和b，gcd(a, b)和gcd(b, a % b)是相同的）

public int gcd(int a, int b) {
    return b != 0? gcd(b, a % b): a;
}

此外还有一种 if + while + 位运算的写法：

public int gcd(int a, int b) {
    if (b != 0) {
        while ((a %= b) != 0 && (b %= a) != 0);
    }
    return a + b;
}

通过使用 System.currentTimeMillis() 来测算程序运行的时间，可以发现后两种写法的耗时要短一些。（后两种的速度差不多都是第一种 while 循环的两倍左右）

最大公约数与质数的关系：通过判断两个或者多个整数之间的公约数只有1，就可以说它们是互质的。

lcm 的写法在 gcd 的基础之上，即两个数相乘然后除最大公约数即为最小公倍数。

public int lcm(int a, int b) {
    return a * b / gcd(a, b);
}

参考资料：
gcd和lcm(最大公约数，最小公倍数)
【C++】gcd函数的写法
D351周赛复盘：美丽下标对数目（互质/数学运算）+数组划分若干子数组

取模运算 %

如果让你计算 $1234 * 6789$ 的个位数，你会如何计算？
由于只有个位数会影响到乘积的个位数，因此 $4 * 9 = 36$ 的个位数 6 就是答案。

将这个结论抽象成数学等式如下：

$\bmod m = ((a \bmod m) + (b \bmod m)) \bmod m$
$\bmod m = ((a \bmod m) * (b \bmod m)) \bmod m$

在这里插入图片描述
参考资料：
https://leetcode.cn/problems/movement-of-robots/solution/nao-jin-ji-zhuan-wan-pai-xu-tong-ji-pyth-we55/

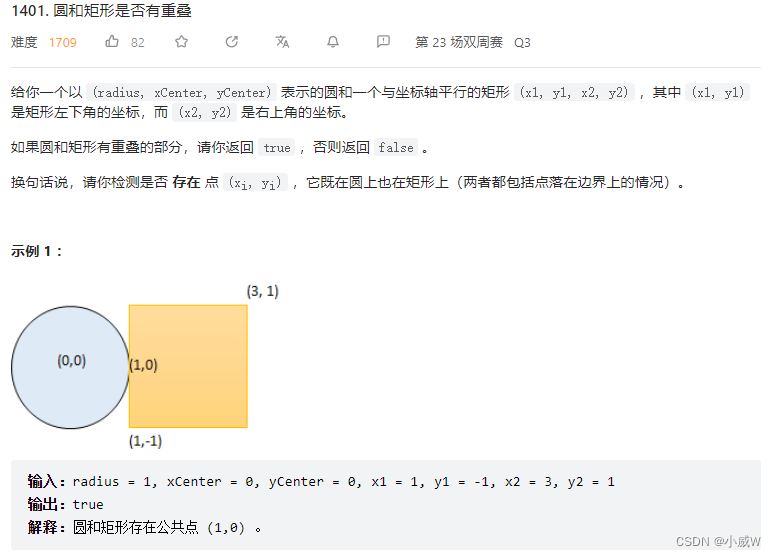
求一个点和一片矩形区域之间的最短距离

以一道题目为例：https://leetcode.cn/problems/circle-and-rectangle-overlapping/

在这里插入图片描述

class Solution {
    public boolean checkOverlap(int radius, int xCenter, int yCenter, int x1, int y1, int x2, int y2) {
        double dist = 0;
        if (xCenter < x1 || xCenter > x2) {
            dist += Math.min(Math.pow(x1 - xCenter, 2), Math.pow(x2 - xCenter, 2));
        }
        if (yCenter < y1 || yCenter > y2) {
            dist += Math.min(Math.pow(y1 - yCenter, 2), Math.pow(y2 - yCenter, 2));
        }
        return dist <= radius * radius;
    }
}