计数排序

以升序排序为例

什么是计数排序

• 计数排序是一个非基于比较的排序算法，该算法于1954年由 Harold H. Seward 提出
• 基本思想：是对于给定的输入序列中的每一个元素x，确定该序列中值小于x的元素的个数（此处并非比较各元素的大小，而是通过对元素值的计数和计数值的累加来确定）。一旦有了这个信息，就可以将x直接存放到最终的输出序列的正确位置上。例如，如果输入序列中只有17个元素的值小于x的值，则x可以直接存放在输出序列的第18个位置上。当然，如果有多个元素具有相同的值时，我们不能将这些元素放在输出序列的同一个位置上，因此，上述方案还要作适当的修改。——百度百科

实现思路

• 根据待排序列的最大值和最小值，向系统申请一块空间

• 空间内每个位置就代表着待排序列最小值到最大值每个数据的映射

• 遍历待排序序列，统计每个数据出现的次数，并记录于申请的空间内

• 最后根据空间中记录的每个数据出现的次数，实现对待排序列的排序

具体步骤

• 我们以数组{101,105,102,107,105,106}为例
• 首先，我们遍历整个乱序序列，找到最大值max，最小值min，从而求出待排序列的数据范围range

for (int i = 0; i < numsSize; i++)
{
    if (nums[i] > max)
        max = nums[i];
    if (nums[i] < min)
        min = nums[i];
}

int range = max - min + 1;

• 向内存中申请range * sizeof(数据类型)大小的空间，并将其初始化为0（这块空间记录的是range范围内每个数据出现的次数，因此初始值为0）

int* count = (int*)malloc(sizeof(int) * range);		//申请内存
memset(count, 0, range * sizeof(int));		//初始化为0

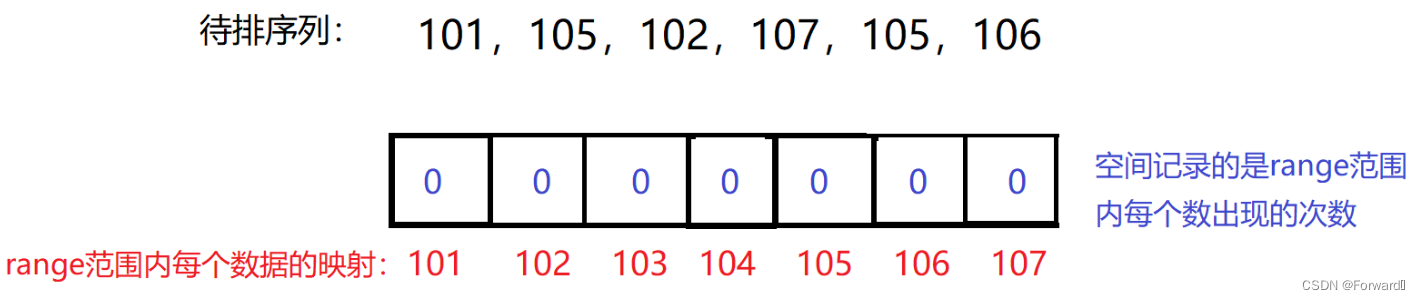
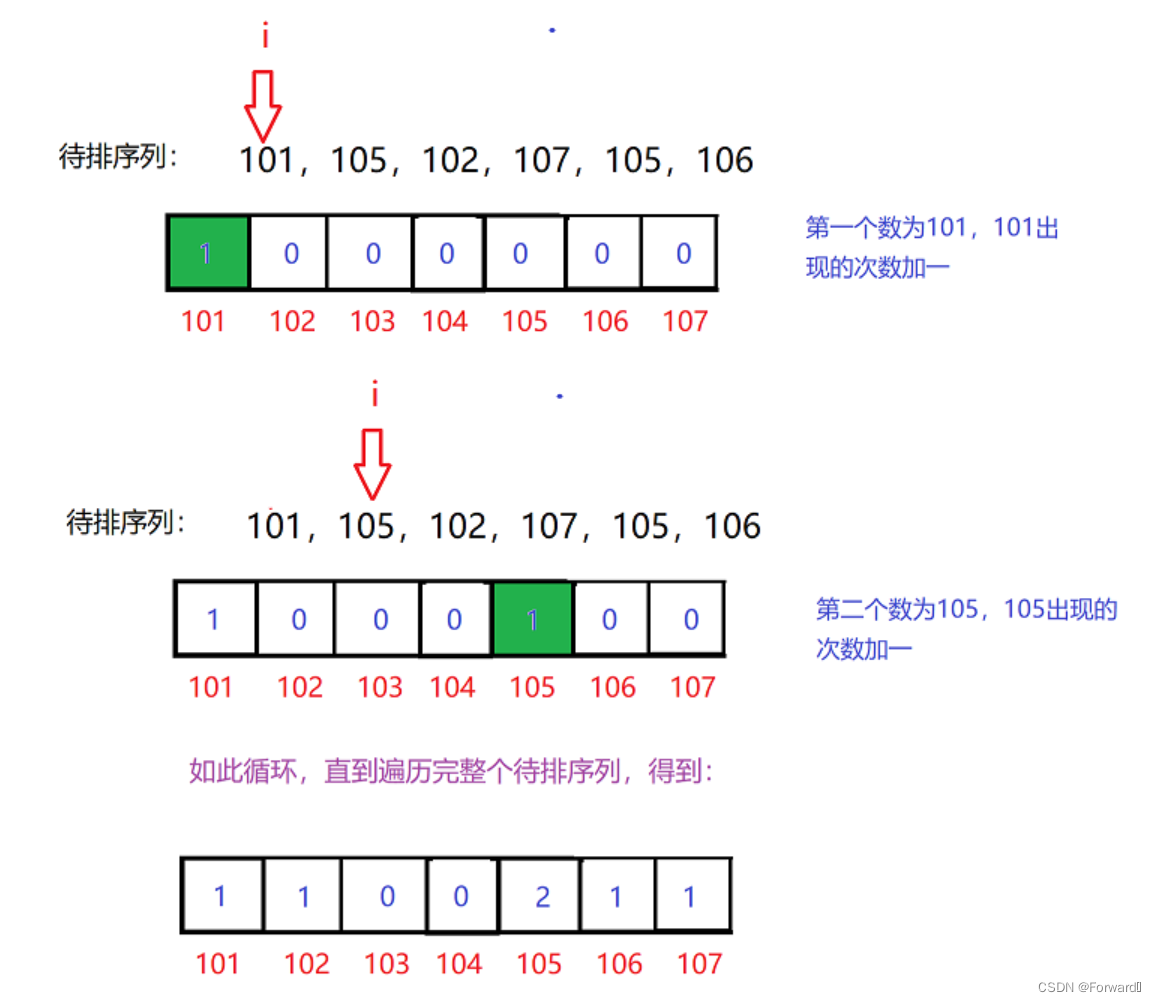
• 遍历乱序序列，记录每个数据出现的次数，并记录到申请的空间中
• 那么问题来了，我们怎么得到每个数据在申请的空间中的位置呢？由上面的分析可以得到吗，空间的第一个位置即下标0处代表着最小值min（例子中的101），102就是101后面的一个数，下标就是102-101 = 1，103就是101后面的第二个数，下标就是103-101 = 2…………，因此数据nums[i]在count中的位置就是nums[i] - min

for (int i = 0; i < numsSize; i++)
		count[nums[i] - min]++;

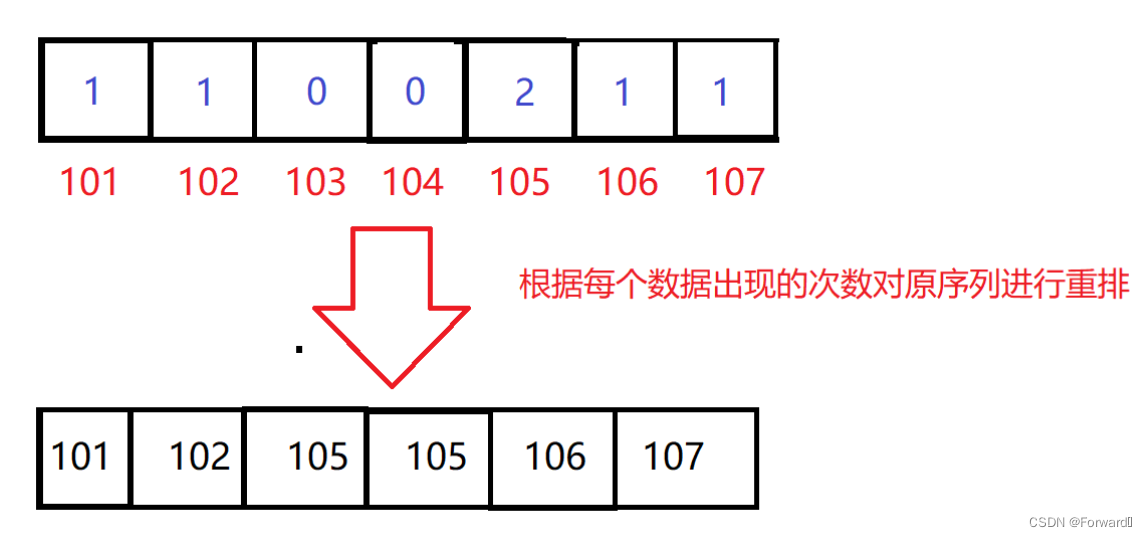
• 由于申请的空间是range范围内从小到大的映射，这已经是一个升序序列，因此最后我们只需要根据空间中记录的每个数据出现的次数，将这些数据重新按顺序放到原序列中就可以实现升序排序了。

int cur = 0;
for (int i = 0; i < range; i++)
{
    while (count[i]--)
        nums[cur++] = i + min;
}

实现代码

void CountSort(int* nums, int numsSize)
{
	int max = nums[0];
	int min = nums[0];

	for (int i = 0; i < numsSize; i++)
	{
		if (nums[i] > max)
			max = nums[i];
		if (nums[i] < min)
			min = nums[i];
	}

	int range = max - min + 1;
	int* count = (int*)malloc(sizeof(int) * range);
	memset(count, 0, range * sizeof(int));

	for (int i = 0; i < numsSize; i++)
		count[nums[i] - min]++;

	int cur = 0;
	for (int i = 0; i < range; i++)
	{
		while (count[i]--)
			nums[cur++] = i + min;
	}
    
    free(count);
}

时间复杂度和局限性

时间复杂度

• 计数排序的时间复杂度为：O(N + K)，其中N为待排序列元素个数，K为待排序列数据范围（即range）
• 是线性的时间复杂度，快于任何比较排序算法

局限性

• 计数排序只能对整数排序
• 如果数据范围range过大，那么不适合用计数排序来排
  • 例如，要对5个数排序，但这20个数的数据范围是一千万，这样像内存申请的空间就会很大，从而造成空间浪费
• 当range > NlogN时，计数排序的效率反而不如基于比较的排序算法，因为堆排序、希尔排序、快速排序、归并排序等排序时间复杂度的理论下限为O(NlogN)