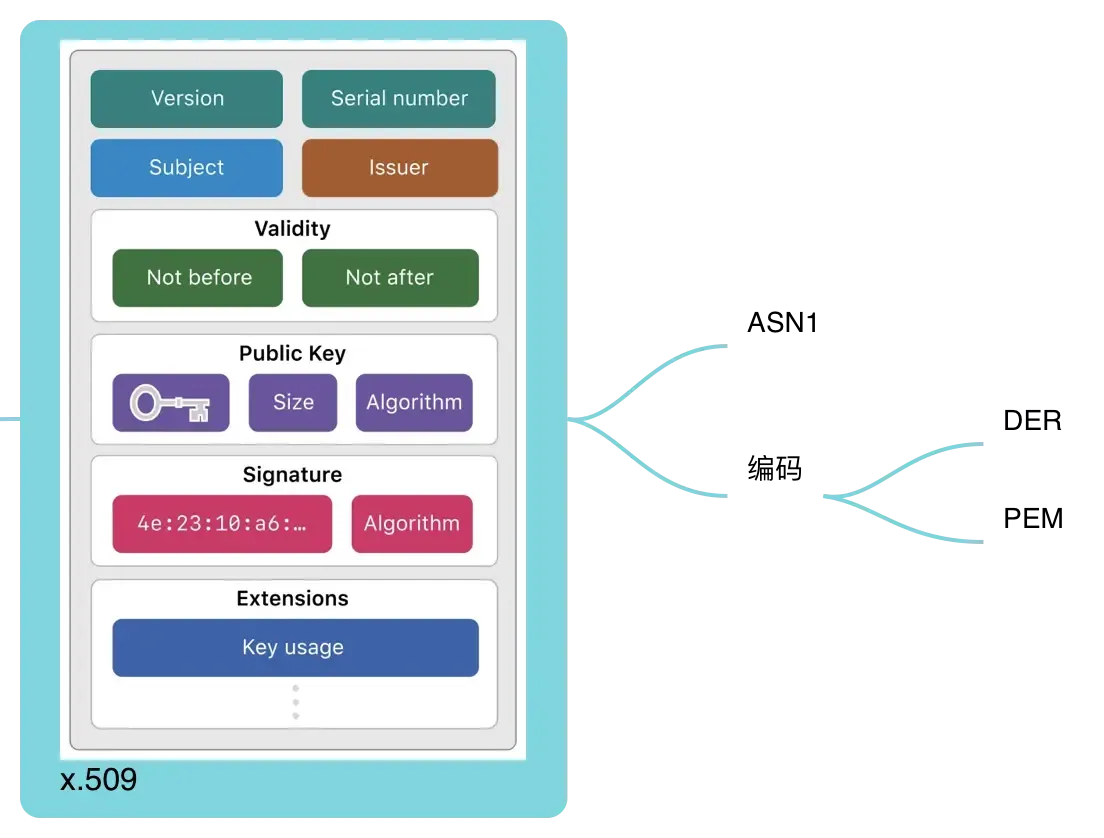
数学建模常用算法之主成分分析
- 引言
- 步骤
- 实例以及代码
引言
主成分分析是一种降维算法,它能将多个指标转换为少数几个主成分,这些主成分是原始变量的线性组合,且彼此之间互不相关,且能反映出原始数据的大部分信息。
一般来说,当研究的问题涉及到多变量且变量之间存在很强的相关性时,我们可以考虑使用主成分分析的方法对数据进行简化。(用较少的新变量替换原来较多的旧变量,并且使这些较少的新变量尽可能多的保留原来变量所反映的信息)
步骤
对数据进行标准化—>计算标准化样本的协方差矩阵—>计算R的特征值和特征向量—>计算主成分贡献率以及累计贡献率——>写出主成分——>根据系数分析主成分代表的意义
-
对数据进行标准化
原始数据:

标准化数据:

-
计算标准化样本的协方差矩阵

-
计算R的特征值和特征向量
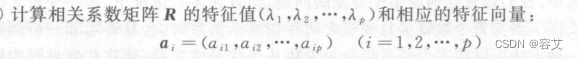
-
计算主成分贡献率以及累计贡献率
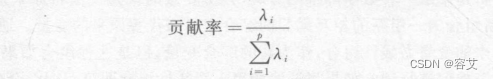
-
写出主成分
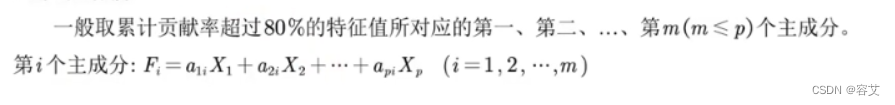
-
根据系数分析主成分代表的意义

实例以及代码
实例:企业综合实力排序
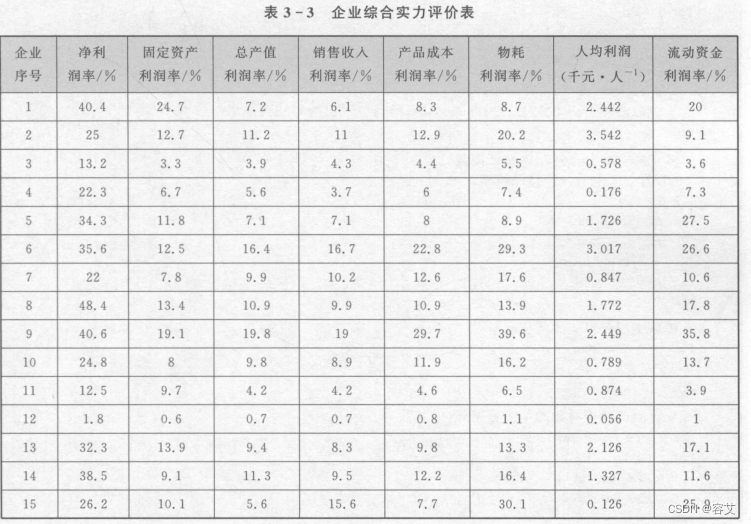
clc
clear all
A = xlsread("Coporation_evaluation.xlsx","B2:I16");
%数据标准化处理
a = size(A,1);
b = size(A,2);
for i=1:b
SA(:,i)=(A(:,i)-mean(A(:,i)))/std(A(:,i));%SA是标准化之后的数据
end
%计算相关系数并计算特征值和特征向量
CM = corrcoef(SA);%相关系数
[V,D]=eig(CM);%V是特征向量矩阵,D是特征值对角矩阵
%disp(D)观察D中数据
for i=1:b
DS(i,1)=D(b+1-i,b+1-i);%按D中数据进行降序排列
end
for i=1:b
DS(i,2)=DS(i,1)/sum(DS(:,1));%计算贡献值
DS(i,3)=sum(DS(1:i,1))/sum(DS(:,1));%计算累积贡献值
end
%选择主成分以及对应的特征向量
T = 0.9;%保留的信息
for i=1:b
if(DS(i,3)>=T)
Com_num=i;
break;
end
end
%提取对应特征向量
for i=1:Com_num
PV(:,i)=V(:,b+1-i);
end
%计算得分
new_score=SA*PV;
for i=1:a
total_score(i,1)=sum(new_score(i,:));%计算总得分
total_score(i,2)=i;%标记编号
end
result_score=[new_score,total_score];
result_score=sortrows(result_score,-4);%按总分降序
disp("特征值,贡献率,累计贡献率")
DS
disp('阀值T对应的主成分数与特征向量:')
Com_num
PV
disp('主成分分数,其中第4列是总得分')
result_score
结果如下
特征值,贡献率,累计贡献率
DS =
5.7361 0.7170 0.7170
1.0972 0.1372 0.8542
0.5896 0.0737 0.9279
0.2858 0.0357 0.9636
0.1456 0.0182 0.9818
0.1369 0.0171 0.9989
0.0060 0.0007 0.9997
0.0027 0.0003 1.0000
阀值T对应的主成分数与特征向量:
Com_num =
3
PV =
0.3334 0.3788 0.3115
0.3063 0.5562 0.1871
0.3900 -0.1148 -0.3182
0.3780 -0.3508 0.0888
0.3853 -0.2254 -0.2715
0.3616 -0.4337 0.0696
0.3026 0.4147 -0.6189
0.3596 -0.0031 0.5452
主成分分数,其中第4列是总得分
result_score =
5.1936 -0.9793 0.0207 4.2350 9.0000
0.7662 2.6618 0.5437 3.9717 1.0000
1.0203 0.9392 0.4081 2.3677 8.0000
3.3891 -0.6612 -0.7569 1.9710 6.0000
0.0553 0.9176 0.8255 1.7984 5.0000
0.3735 0.8378 -0.1081 1.1033 13.0000
0.4709 -1.5064 1.7882 0.7527 15.0000
0.3471 -0.0592 -0.1197 0.1682 14.0000
0.9709 0.4364 -1.6996 -0.2923 2.0000
-0.3372 -0.6891 0.0188 -1.0075 10.0000
-0.3262 -0.9407 -0.2569 -1.5238 7.0000
-2.2020 -0.1181 0.2656 -2.0545 4.0000
-2.4132 0.2140 -0.3145 -2.5137 11.0000
-2.8818 -0.4350 -0.3267 -3.6435 3.0000
-4.4264 -0.6180 -0.2884 -5.3327 12.0000
结果:第9家最强,第12家最弱





![[230608] 阅读TPO58汇总|7:30-9:00+17:05](https://img-blog.csdnimg.cn/cba0e007d19c40d48231d90ce59106c6.png)