系列文章目录

第一章 AlexNet网络详解

第二章 VGG网络详解

第三章 GoogLeNet网络详解 

第四章 ResNet网络详解 

第五章 ResNeXt网络详解 

第六章 MobileNetv1网络详解 

第七章 MobileNetv2网络详解 

第八章 MobileNetv3网络详解 

第九章 ShuffleNetv1网络详解 

第十章 ShuffleNetv2网络详解 

第十一章 EfficientNetv1网络详解 

第十二章 EfficientNetv2网络详解 

第十三章 Transformer注意力机制

第十四章 Vision Transformer网络详解 

第十五章 Swin-Transformer网络详解 

第十六章 ConvNeXt网络详解 

第十七章 RepVGG网络详解 

第十八章 MobileViT网络详解 

文章目录

• 0. 摘要
• 1. 前言
• 2.   
  • 1.  
  • 2.
• 总结

---

0、摘要

主导的序列转换模型基于包含编码器和解码器的复杂递归或卷积神经网络。表现最好的模型还通过注意机制将编码器和解码器连接起来。我们提出了一种新的简单网络架构——Transformer，仅基于注意机制，完全放弃了递归和卷积。在两个机器翻译任务上的实验表明，这些模型在质量方面更优秀，同时更具并行性，需要的训练时间显著减少。在WMT 2014英德翻译任务中，我们的模型达到了28.4 BLEU分数，比现有最佳结果（包括集合模型）高出2 BLEU分数。在WMT 2014英法翻译任务中，我们的模型在8个GPU上训练3.5天后，建立了一个新的单模型最先进的BLEU分数记录（41.0），其训练成本只是文献中最佳模型的一小部分。

 

1、前言

递归神经网络、长期短期记忆[12]和门控循环[7]神经网络已经被确立为序列建模和转换问题（如语言建模和机器翻译[29,2,5]）的最先进方法。此后，已经进行了大量的努力，推动递归语言模型和编码器-解码器架构的极限[31,21,13]。

递归模型通常会将计算沿着输入和输出序列的符号位置进行分解。将位置与计算时间步对齐，生成隐藏状态序列ht作为先前隐藏状态ht−1和位置t的输入的函数。这种固有的顺序性质使得训练示例内部无法并行化，在处理较长序列长度时变得至关重要，因为内存限制会限制跨示例进行分组。最近的工作通过分解技巧[18]和条件计算[26]实现了计算效率的显着提高，同时在后一种情况下提高了模型性能。然而，顺序计算的基本约束仍然存在。注意力机制已经成为在各种任务中引人注目的序列建模和转换模型的重要组成部分，使得可以对依赖性进行建模，而不考虑它们在输入或输出序列中的距离[2,16]。但除了少数情况[22]之外，这些注意力机制通常与递归网络一起使用。在这项工作中，我们提出了Transformer，这是一种完全避免递归并完全依赖于注意机制来绘制输入和输出之间全局依赖关系的模型架构。Transformer允许更多的并行化，并经过仅在8个P100 GPU上训练约12个小时后可以达到翻译质量的新水平。

2 背景

减少串行计算的目标也是 Extended Neural GPU [20]、ByteNet [15] 和 ConvS2S [8] 的基础，它们都使用卷积神经网络作为基本构件，在所有输入和输出位置并行计算隐藏表示。在这些模型中，在任意两个输入或输出位置之间关联信号所需的操作数随着位置之间的距离增加而增加，对于 ConvS2S 是线性的，对于 ByteNet 是对数的。这使得学习远距离位置之间的依赖关系变得更加困难 [11]。在 Transformer 中，这被减少到恒定数量的操作，尽管由于平均注意加权位置而导致有效分辨率降低的代价，我们通过第 3.2 节中所述的 Multi-Head Attention 进行抵消。 自注意力（有时称为内部注意力）是一种关注机制，它关联单个序列的不同位置以计算该序列的表示。自注意力已经成功地用于各种任务，包括阅读理解、抽象概括、文本蕴含和学习任务无关的句子表示 [4,22,23,19]。端到端的存储器网络基于循环注意机制，而不是序列对齐循环，已经表现出在简单语言问答和语言建模任务上表现良好 [28]。然而，据我们所知，Transformer 是第一种完全依赖自注意力来计算其输入和输出表示而不使用序列对齐 RNN 或卷积的转换模型。在接下来的章节中，我们将描述 Transformer，解释自注意力并讨论它在[14,15]和[8]模型中的优势。

2.正文分析

3 模型架构

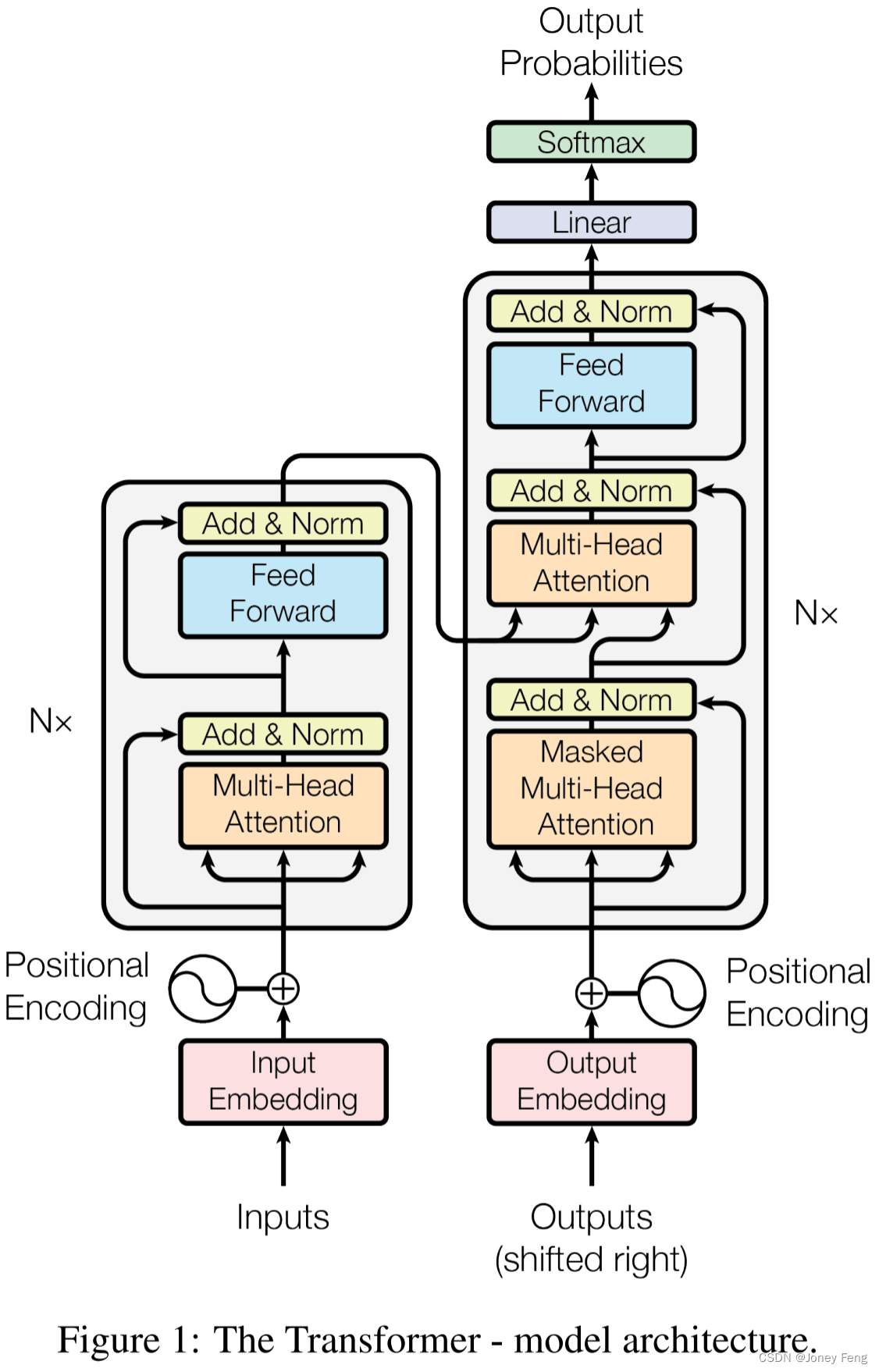
大多数竞争力的神经序列转导模型都具有编码器-解码器结构[5,2,29]。在这种情况下，编码器将符号表示的输入序列（x1; :::; xn）映射到连续表示序列z = （z1; :::; zn）。给定z，解码器随后一次生成一个符号输出序列（y1; :::; ym）。在每个步骤中，模型都是自回归的[9]，在生成下一个符号时使用先前生成的符号作为附加输入。Transformer使用堆叠自注意力和逐点，完全连接的层来实现编码器和解码器，分别显示在图1的左半部分和右半部分。

 3.1 编码器和解码器堆栈编码器：

编码器由N = 6个相同层堆叠而成。每个层有两个子层。第一个是多头自我关注机制，第二个是简单的位置连接全连接前馈网络。我们在每个子层周围采用残差连接[10]，然后进行层规范化[1]。也就是说，每个子层的输出是 LayerNorm（x + Sublayer（x）），其中 Sublayer（x）是子层本身实现的功能。为了方便这些残差连接，模型中的所有子层以及嵌入层都产生512维的输出。

解码器：解码器也由N = 6个相同的层组成。除了每个编码器层中的两个子层外，解码器还插入了第三个子层，该子层对编码器堆栈的输出执行多头关注。与编码器类似，我们在每个子层周围采用残差连接，然后进行层规范化。我们还修改了解码器堆栈中的自我关注子层，以防止位置关注后续位置。这种屏蔽结合事实，即输出嵌入被偏移一个位置，确保位置i的预测只能依赖于小于i的已知输出。

3.2 注意力机制 注意力机制可以被描述为将一个查询和一组键值对映射到一个输出，其中查询、键、值和输出都是向量。输出被计算为值的加权和，其中分配给每个值的权重是由查询与相应键的兼容函数计算得出的。

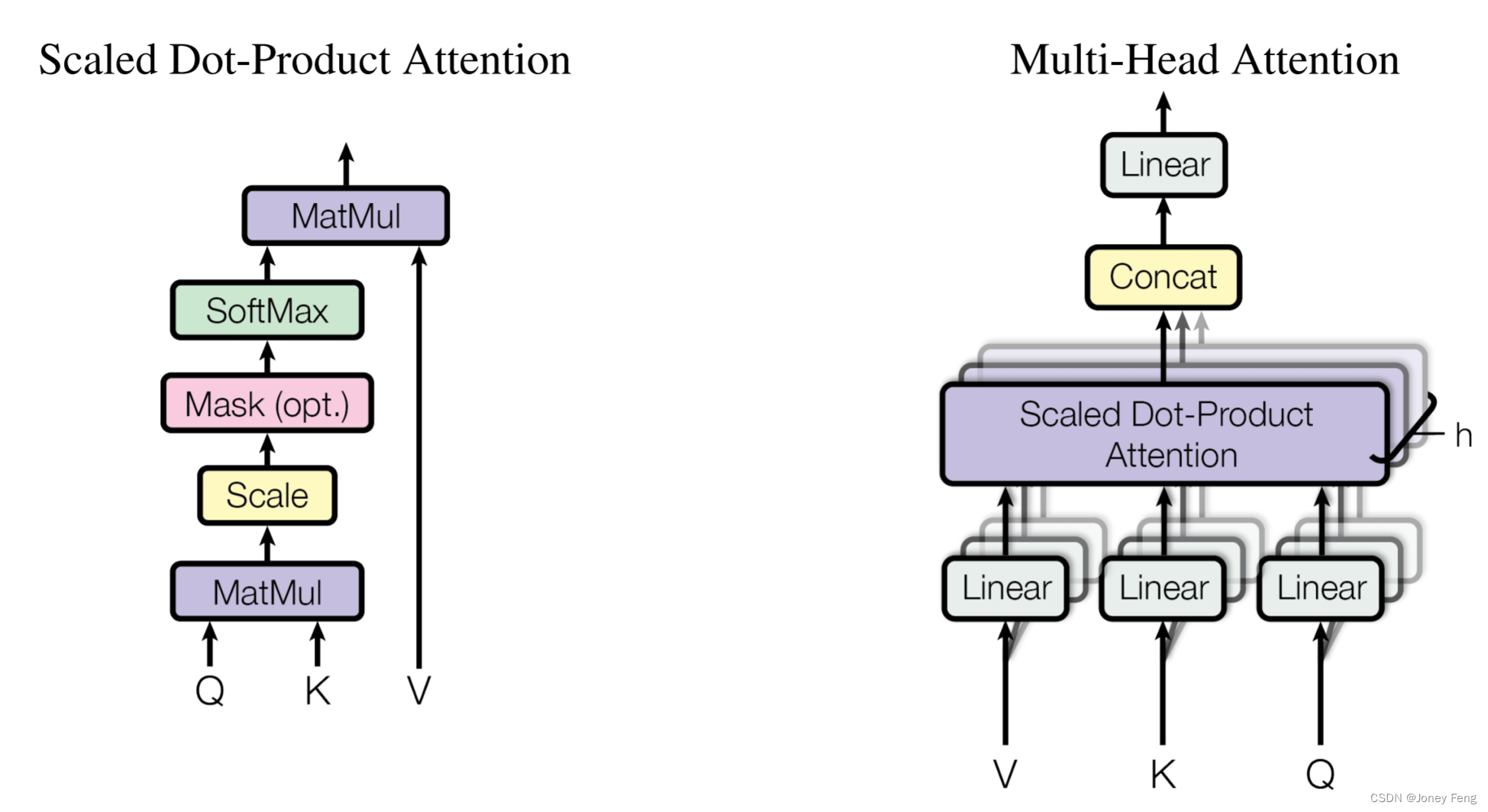
 (图2: (左) 缩放点积自注意力. (右) 多头注意力由多个并行运行的注意力层组成)

3.2.1 缩放点积注意力

我们将我们特定的注意力称为“缩放点积注意力”（图2）。输入由查询和维度为dk的键以及维度为dv的值组成。我们计算查询与所有键的点积，将每个点积除以pdk，并应用softmax函数以获得值的权重。在实践中，我们同时在一组查询上计算注意力函数，将它们打包成一个矩阵Q。键和值也被打包成矩阵K和V。我们计算输出矩阵如下:Attention(Q;K;V )=softmax(QK pdkT )V (1)两种最常用的注意力函数是加性注意力[2]和点积（乘法）注意力。点积注意力与我们的算法相同，除了缩放因子p1dk。加性注意力使用具有单个隐藏层的前馈神经网络计算兼容性函数。虽然在理论复杂度上两者相似，但是在实践中，点积注意力更快速和更节省空间，因为它可以使用高度优化的矩阵乘法代码来实现。对于较小的dk值，这两种机制的表现相似，但对于较大的dk值，加性注意力在没有缩放的情况下优于点积注意力[3]。我们怀疑，对于大的dk值，点积过大，将softmax函数推入具有极小梯度的区域4。为了抵消这种效应，我们将点积缩放为p1dk。

3.2.2 多头注意力

我们发现，与使用 dmodel维键、值和查询执行单一的注意函数相比，将查询、键和值进行 h 次不同的学习线性变换，分别从 dmodel 维投影到 dk，dk 和 dv 维，可以更有益地运用信息。然后我们对每个映射版本的查询、键和值并行执行注意函数，产生 dv 维输出值。这些值被串联在一起，再次进行投影，得到最终的值，如图 2 所示。多头注意力使模型能够同时查看来自不同表示子空间不同位置的信息。使用单个注意头时，平均会阻碍这一过程。MultiHead(Q;K;V )=Concat(head1;:::;headh)WO，其中 headi=Attention(QWiQ;KWiK;V WiV)。投影是参数矩阵WiQ 2 Rdmodel×dk,WiK 2 Rdmodel×dk,WiV 2 Rdmodel×dv和 WO 2 Rhdv×dmodel。在本次工作中，我们使用了8个并行的注意力层或头。对于每个头，我们使用 dk=dv=dmodel=h=64。由于每个头的减少维度，总的计算成本与单头注意力的完整维度相似。

3.2.3 我们模型中注意力的应用

Transformer 在三个不同的方面使用多头注意力：

•在“编码解码注意力”层中，查询（queries）来自上一个解码（decoder）层，而存储的键（keys）和值（values）来自编码器（encoder）的输出。这允许解码器中的每个位置关注输入序列中的所有位置。这类似于序列到序列模型（如[31, 2, 8]）中的典型编码解码注意力机制。

•编码器包含自注意力层。在自注意力层中，所有的键、值和查询都来自同一个位置，即编码器中的上一层的输出。编码器中的每个位置都可以关注编码器中先前一层的所有位置。

•同样地，解码器中的自注意力层允许解码器中的每个位置关注到该位置及之前的所有位置。我们需要防止左向信息在解码器中流动，以保留自回归属性。我们通过在缩放的点积注意力中将所有值中对应非法连接的输入设置为-1来实现这一点。详见图2。

3.3.3 按位置前馈网络

除了注意力子层之外，我们编码器和解码器中的每个层都包含全连接的前馈网络，该网络对每个位置分别和相同地应用。它由两个线性转换和一个 ReLU 激活层组成。FFN（x）=max（0，xW1 + b1）W2 + b2（2） 虽然线性变换在不同的位置上都是相同的，但它们在不同的层之间使用不同的参数。另一种描述方法是使用内核大小为1的两个卷积。输入和输出的维度为dmodel =512，内部层的维度为dff=2048。

3.4 嵌入和Softmax

与其他序列转导模型类似，我们使用学习到的嵌入将输入标记和输出标记转换为维度为dmodel的向量。我们还使用通常的学习线性转换和softmax函数将解码器输出转换为预测的下一个标记的概率。在我们的模型中，我们在两个嵌入层和预softmax线性变换之间共享相同的权重矩阵，类似于[24]。在嵌入层中，我们将这些权重乘以pdmodel。

3.5 位置编码

由于我们的模型不包含重复和卷积，为了让模型利用序列的顺序，我们必须注入一些关于令牌在序列中相对或绝对位置的信息。为此，我们在编码器和解码器堆栈的底部添加“位置编码”到输入嵌入中。位置编码与嵌入相同的维度dmodel,因此可以将两者相加。有许多学习和固定的位置编码选择[8]。在这项工作中，我们使用不同频率的正弦和余弦函数：PE（pos；2i）=sin（pos=100002i=dmodel）PE（pos；2i+1）=cos（pos=100002i=dmodel），其中pos是位置，i是维度，即位置编码的每个维度对应一个正弦波。波长从2π到10000·2π形成等比数列。我们选择这个函数，因为我们假设它可以让模型轻松地通过相对位置来学习注意力，因为对于任何固定偏移k，PEpos+k可以表示为PEpos的线性函数。我们还尝试使用学习的位置嵌入[8]，并发现两个版本产生了几乎相同的结果（见表3行（E））。我们选择正弦曲线版本，因为它可以允许模型推广到比训练时遇到的序列长度更长的序列。

如表1所示，自我关注层将所有位置连接到一个恒定数量的顺序执行操作，而循环层则需要O（n）个顺序执行操作。在计算复杂性方面，当序列长度n小于表示维度d（这通常是机器翻译中最先进模型使用的句子表示，例如单词片段[31]和字节对[25]表示）时，自我关注层比循环层更快。为了提高涉及非常长序列的任务的计算性能，自我关注可以仅考虑输入序列中以相应输出位置为中心的大小为r的邻域。这将增加最大路径长度为O（n=r）。我们计划在未来的工作中进一步研究这种方法。

4为什么需要自我关注：

在本节中，我们比较自我关注层与常用于将一个可变长度的符号表示序列（x1；...；xn）映射到另一个等长度序列（z1；...；zn）的递归和卷积层的各个方面，其中xi；zi 2 Rd，如典型序列传导编码器或解码器中的隐藏层。在使用自我关注的动机下，我们考虑三个需要满足的条件。第一是每层的总计算复杂度。第二是可以并行计算的计算量，按所需的最少顺序操作数量来衡量。第三是网络中长距离依赖之间的路径长度。在许多序列传导任务中，学习长距离依赖是一个关键挑战。影响学习此类依赖关系能力的一个关键因素是向前和向后信号在网络中所需经过的路径长度。这些输入和输出序列之间的任意位置组合之间路径越短，学习长距离依赖关系就越容易[11]。因此，我们还比较了由不同层类型组成的网络中任意两个输入和输出位置之间的最大路径长度。

当卷积层的核宽度k<n时，单个卷积层无法连接所有输入和输出位置的对应关系。为了解决这个问题，需要堆叠O(n/k)个卷积层（对于连续的卷积核情况），或者堆叠O(logk(n))个卷积层（对于扩张卷积情况），这会增加网络中任意两个位置之间最长路径的长度。相比循环层，卷积层通常更加昂贵，因为需要乘以一个系数k。但是，基于可分离卷积的方法可以显著降低复杂度，变为O(k·n·d+n·d^2)。即使在k=n的情况下，可分离卷积的复杂度仍然等于自注意力层和逐点前馈层的组合，这也是我们模型中采用的方法。作为附带好处，自注意力可以产生更可解释的模型。我们检查了模型中的注意力分布，并在附录中呈现和讨论了一些例子。不仅单个注意力头明显学习了不同的任务，许多注意力头似乎表现出与句子的句法和语义结构相关的行为。

5 训练

本节介绍我们的模型培训技术。

5.1 培训数据与分组

我们使用了包含约450万句子对的标准 WMT 2014 英德数据集进行训练。句子采用字节对编码进行编码[3]，使用约37000个共享源/目标单词表。对于英法，我们使用规模更大的WMT 2014 英法数据集，包含 3600万个句子，并将标记分成了32000个词素[31]。句子对按照近似序列长度分组，每个训练批次含有大约25000个源标记和25000个目标标记的句子对。

5.2 硬件和日程

我们在一台拥有8个 NVIDIA P100 GPU的机器上进行了模型训练。对于使用本文中描述的超参数的基础模型，每个训练步骤耗时约为0.4秒。我们总共训练了100,000步或12小时。对于大模型（按表3的底部行描述），每个步骤的时间为1.0秒。大模型训练了300,000步（3.5天）。

5.3 优化器 我们使用了Adam优化器[17]，β1 =0.9，β2 =0.98，ε=10−9。我们根据以下公式调整了学习率：lrate =d−0.5 model ·min(step_num−0.5;step_num ·warmup_steps−1.5)(3)，其中d为模型尺度，step_num为当前步数，warmup_steps=4000。这相当于在线性增加学习率的前warmup_steps个训练步骤内，以及在其后按照步数的倒数平方根成比例递减。

5.4 正则化

我们在训练过程中采用了三种类型的正则化： 残差随机失活 在每个子层的输出加到子层输入和正则化之前，我们对其应用失活[27]。另外，我们对编码器和解码器堆栈中的嵌入和位置编码的总和也进行了失活处理。对于基础模型，我们使用Pdrop =0.1的失活率。 标签平滑化 在训练过程中，我们采用了值为ls =0.1的标签平滑化[30]。这会降低困惑度，因为模型会变得更加不确定，但可以提高准确性和BLEU分数。

6 结果

6.1 机器翻译 在 WMT 2014 英译德任务中，大型 Transformer 模型（表2 中的 Transformer（big））的表现优于之前报告的最佳模型（包括集成模型）超过 2.0 BLEU，创下了 28.4 的最新 BLEU 得分纪录。该模型的配置列在表3 的底行中。训练使用 8 块 P100 GPU 进行了 3.5 天。即使是我们的基本模型，也超过了以前发表的所有模型及集成模型，在培训成本的一小部分的情况下。在 WMT 2014 英译法任务中，我们的大型模型取得了 41.0 的 BLEU 得分，在以前发表的所有单一模型之上，而培训成本还不到以前最新模型的四分之一。英译法的 Transformer（big）模型使用了丢弃率 Pdrop = 0.1，而非 0.3。对于基本模型，我们使用了平均最后 5 个检查点得到的单一模型，这些模型是以 10 分钟间隔编写的。对于大型模型，我们平均最后的 20 个检查点。我们使用了带有 4 个束搜索和长度惩罚 α = 0.6（31）的搜索。这些超参数是通过开发集的实验选择的。我们将推断期间的最大输出长度设置为输入长度 +50，但尽可能早地终止（31）。表2 总结了我们的结果，并将我们的翻译质量和培训成本与文献中的其他模型架构进行了比较。我们估计训练模型使用的浮点操作数量，方法是将训练时间、GPU 数量和每个 GPU 的单精度浮点容量的可持续估计相乘（5）。

6.2 模型变异

为了评估Transformer不同组件的重要性，我们以不同方式变异了我们的基础模型，在开发集newstest2013上测量了英德翻译的性能变化。我们使用了前一节中描述的beam search，但未进行检查点平均化。我们在表3中呈现了这些结果。在表3的(A)行中，我们变化了注意力头数以及注意力键和值的维度，保持了计算量不变，如3.2.2节所述。虽然单头注意力比最佳设置差0.9 BLEU，但过多的头数也会降低质量。

在表3的行（B）中，我们观察到减少注意键大小dk会影响模型质量。这表明确定兼容性并不容易，而比点积更复杂的兼容性函数可能会更有益。我们进一步观察到，如预期所料，模型越大越好，在（C）和（D）行中进行投放可以有效避免过拟合。在行（E）中，我们用学习的位置嵌入替换了我们的正弦位置编码，并观察到几乎与基准模型相同的结果。

表1：不同层类型的最大路径长度、每层复杂度和最小顺序操作数量。n为序列长度，d为表示维度，k为卷积核大小，r为受限自注意力邻域大小

Table 1:Maximum path lengths,per-layer complexity and minimum number of sequential operations for different layer types.n is the sequence length,d is the representation dimension,k is the kernel size of convolutions and r the size of the neighborhood in restricted self-attention

Layer Type	Complexity per Layer	Sequential Operations	Maximum Path Length
Self-Attention	O(n2.d)	O(1)	O(1)
Recurrent	O(n.d2)	O(n)	O(n)
Convolutional	O(k.n.d2)	O(1)	O(logk(n))
Self-Attention(restricted)	O(r.n.d)	O(1)	O(n/r)

顺序操作是指必须按特定顺序执行一系列操作。这些操作相互依赖，不能同时执行。例如，如果您想要烤蛋糕，需要按照顺序执行几个步骤 - 准备面糊，倒入烤盘，然后放入烤箱烤制。

最大路径长度是指连接两个节点的图形或网络中的最长路径。最大路径长度是通过计算起始节点和终止节点之间边缘的长度之和得出的。它可以用于确定网络或系统的效率，因为较长的路径可能需要更多的时间和资源才能完成。在计算机科学中，可以使用最大路径长度来优化算法的性能，从而减少执行它们所需的时间。

这个表格主要是用来比较不同类型的神经网络层的复杂度和最大路径长度，以及每个层类型所需的最少顺序操作数。其中，n表示序列长度，d表示表示维度，k表示卷积核大小，r表示限制性自注意力机制中邻域的大小。

表格说明了不同类型的神经网络层有着不同的复杂度和最大路径长度。其中，Self-Attention的复杂度是O(n2·d)，最大路径长度和最少顺序操作数都是O(1)；Recurrent层的复杂度是O(n·d2)，最大路径长度和最少顺序操作数都是O(n)；Convolutional层的复杂度是O(k·n·d2)，最大路径长度是O(logk(n))，最少顺序操作数是O(1)；Restricted Self-Attention层的复杂度是O(r·n·d)，最大路径长度是O(n=r)，最少顺序操作数是O(1)。

综上所述，这个表格表明了不同类型的神经网络层的复杂度和最大路径长度有所不同。其中Self-Attention层的复杂度最高，但是最大路径长度和最少顺序操作数最小；Convolutional层的复杂度相对较低，但是最大路径长度较大；Restricted Self-Attention层的复杂度和最大路径长度都比Self-Attention层低，但是最少顺序操作数比Self-Attention层高；Recurrent层的复杂度和最大路径长度都比较高，但是最少顺序操作数和序列长度成正比。这些信息可以帮助我们在构建神经网络时选择合适的层类型，以满足不同的需求。

Self-Attention层是一种基于注意力机制的神经网络层，适用于序列到序列的任务，如机器翻译、文本生成等。它通过对输入序列中不同位置之间的关系进行建模，来实现对输入的理解和编码。在Self-Attention层中，每个输入位置都与其他输入位置计算相似度，并按照相似度权重对其他输入位置进行加权求和，得到每个位置的向量表示。

Recurrent层是一种经典的神经网络层，适用于处理序列数据。它通过在时间步之间共享权重，来实现对序列的建模和编码。在Recurrent层中，每个时间步的输入和前一时间步的状态向量进行合并，经过一个非线性变换后得到当前时间步的状态向量。

Convolutional层是一种常用的神经网络层，适用于处理图像和序列数据。它通过卷积核在输入上进行滑动，来提取局部特征，并通过池化操作来减小特征图的大小。在序列数据中，卷积核沿着时间轴进行滑动。

Self-Attention (restricted)层是一种限制性自注意力机制，是对Self-Attention层的改进。在Self-Attention (restricted)层中，每个位置只与它周围一定范围内的位置计算相似度，而不是与所有位置计算相似度。这种限制可以减少计算量和内存占用，同时保持较好的性能。

表2：Transformer在英德和英法newstest2014测试中比之前最先进的模型实现了更好的BLEU得分，并且训练成本只占一小部分。

Table 2:The Transformer achieves better BLEU scores than previous state-of-the-art models on the English-to-German and English-to-French newstest2014 tests at a fraction of the training cost.

Model	BLEU		Training Cost(FLOPs)
	EN-DE	EN-FR	EN-DE	EN-FR
ByteNet	23.75	-	-
Deep-Att+PosUnk	-	39.2	-	1.0·1020
GNMT+RL	24.6	39.92	2.3·1019	1.4·1020
ConvS2S	25.16	40.46	9.6·1018	1.5·1020
MoE	26.03	40.56	2.0·1019	1.2·1020
Deep-Att+PosUnk Ensemble	-	40.4	-	8.0·1020
GNMT+RL Ensemble	26.30	41.16	1.8·1020	1.1·1021
ConvS2S Ensemble	26.36	41.29	7.7·1019	1.2·1021
Transformer(base model)	27.3	38.1	3.3·1018
Transformer(big)	28.4	41.0	2.3·1018

这个表格主要展示了在英语到德语和英语到法语新闻测试集上，各个神经机器翻译模型的BLEU分数和训练成本的比较。BLEU分数是机器翻译中广泛使用的评估指标，用于衡量机器翻译输出与人工参考翻译之间的相似程度，数值范围为0到100。训练成本是指训练模型所需的计算资源，通常用浮点操作次数(FLOPs)来衡量。

各个参数的含义和作用如下：

Model: 模型名称

BLEU: 在英语到德语和英语到法语新闻测试集上的BLEU分数

Training Cost: 训练成本，通常用浮点操作次数(FLOPs)来衡量。表示训练模型所需的计算资源。

EN-DE: 表示在英语到德语翻译任务上的性能指标。

EN-FR: 表示在英语到法语翻译任务上的性能指标。

从表格可以看出，Transformer模型在英语到德语和英语到法语翻译任务上取得了更好的BLEU分数，且训练成本只有其他模型的一小部分。在各个模型中，Deep-Att+PosUnk Ensemble和GNMT+RL Ensemble的BLEU分数也比较高，但训练成本较高。此外，MoE模型的BLEU分数也不错，但训练成本较高。另外，ConvS2S模型的BLEU分数较低，且训练成本较高。

综上所述，Transformer模型在神经机器翻译任务中具有较好的性能和效率。

表3：Transformer 架构的变化。未列出的值与基础模型相同。所有指标都是根据英德翻译开发集 newstest2013 计算得出的。列出的困惑度是按照我们的字节对编码每个单词拼合计算得出的，并且不应与按单词计算的困惑度进行比较。

Table 3:Variations on the Transformer architecture.Unlisted values are identical to those of the base model.All metrics are on the English-to-German translation development set,newstest2013.Listed perplexities are per-wordpiece,according to our byte-pair encoding,and should not be compared to per-word perplexities.

	N	dmodel	dff	h	dk	dv	Pdrop	€ls	Train steps	PPL(dev)	BLEU(dev)	Params ×106
base	6	512	2048	8	64	64	0.1	0.1	100k	4.92	25.8	65
(A)				1	512					5.29	24.9
				4	128					5.00	25.5
				16	32					4.91	25.8
				32	16					5.01	25.4
(B)					16					5.16	25.1	58
					32					5.01	25.4	60
(C)	2									6.11	23.7	36
	4									5.19	25.3	50
	8									4.88	25.5	80
		256			32	32				5.75	24.5	28
		1024			128	128				4.66	26.0	168
			1024							5.12	25.4	53
			2096							4.75	26.2	90
(D)							0.0			5.77	24.6
							0.2			4.95	25.5
								0.0		4.67	25.3
								0.2		5.47	25.7
(E)	Positional embedding instead of sinusoids									4.92	25.7
big	6	1024	4096	16			0.3		300k	4.33	26.4	213

在表格3的B行中，我们观察到减小注意力键的大小会损害模型的质量。这表明确定兼容性并不容易，比点积更复杂的兼容性函数可能有益。我们进一步观察到，在C和D行中，随着模型变得更大，效果更好。丢弃技巧对避免过拟合也非常有帮助。在E行中，我们将正弦位置编码替换为学习得到的位置嵌入，观察到与基准模型几乎相同的结果。

这个表格主要展示了在Transformer模型架构的不同变体中，各个超参数对翻译性能的影响。表格中的各个变体都是在英语到德语翻译任务的开发集newstest2013上进行评估的。各个参数的含义和作用如下：

N: 表示Transformer中encoder和decoder中多头自注意力机制中的注意力头数。

dmodel: 表示Transformer中encoder和decoder中的词向量维度，也是注意力机制中Q、K、V矩阵的维度。

dff: 表示Transformer中encoder和decoder中全连接层的隐层单元数。

h: 表示Transformer中encoder和decoder中多头自注意力机制的注意力头数。

dk: 表示Transformer中encoder和decoder中Q、K矩阵的维度，通常等于dmodel/h。

dv: 表示Transformer中encoder和decoder中的V矩阵的维度，通常等于dmodel/h。

Pdrop: 表示Transformer中encoder和decoder中dropout的概率。

€ls: 表示Transformer中decoder中的label smoothing的系数。

train steps: 表示训练模型所需的步数。

PPL: 表示在开发集上的perplexity，用于衡量模型对数据的拟合程度。值越小表示模型性能越好。

BLEU: 表示在开发集上的BLEU分数。

params: 表示模型的参数数量。

steps: 表示在开发集上的训练步数。

从表格可以看出，不同的超参数组合对翻译性能产生了不同的影响。例如，将注意力头数h增加到16，可以显著提高BLEU分数；将词向量维度dmodel增加到1024，也可以提高BLEU分数。此外，采用不同的position embedding方法，也会对翻译性能产生一定的影响。总体来说，通过调整不同的超参数，可以优化Transformer模型的性能。

总结

结论：本文介绍了Transformer这一基于注意力完全替代Encoder-Decoder中常见的循环层的序列传递模型。在翻译任务中，与基于循环或卷积层的结构相比，Transformer训练速度更快。在WMT 2014英德和英法翻译任务中，我们取得了最新的最优性能。在前一个任务中，我们的最佳模型甚至胜过以前报告的所有集合。我们对基于注意力的模型的未来感到兴奋，并计划将其应用于其他任务。我们计划将Transformer扩展到涉及文本以外的输入和输出模态的问题，并研究局部、受限制的注意力机制以有效处理诸如图像、音频和视频等大型输入和输出。使生成过程不那么序列化是我们另一个研究目标。我们用于训练和评估模型的代码可在 "https://github.com/tensorflow/tensor2tensor"上获得。