堆——“数据结构与算法”

news2024/12/30 2:05:51

各位CSDN的uu们你们好呀，今天小雅兰的内容仍旧是二叉树，此刻分享的内容是一种特殊的二叉树，也就是堆了。下面，让我们进入堆的世界吧！！！

typedef int HeapDataType;
typedef struct Heap
{
	HeapDataType* a;
	int size;
	int capacity;
}Heap;

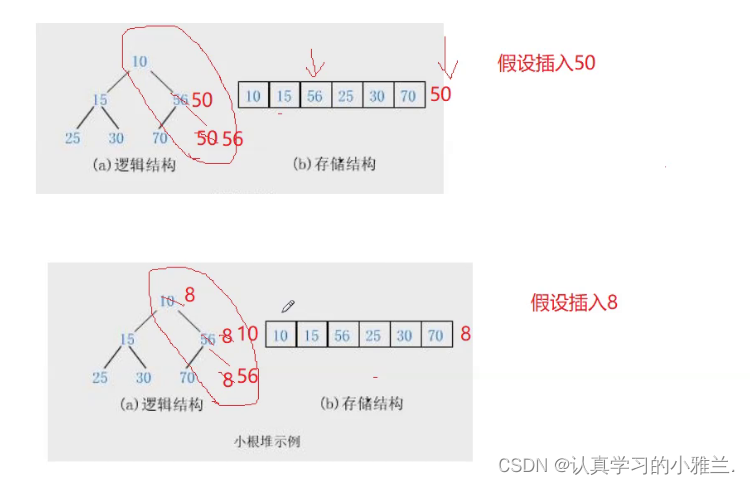
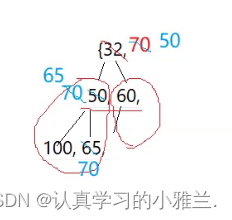
插入数据

需要用到一种特别的算法——向上调整算法

//插入数据
void HeapPush(Heap* php, HeapDataType x)
{
	assert(php);
	//扩容
	if (php->size == php->capacity)
	{
		int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HeapDataType* tmp = (HeapDataType*)realloc(php->a, newcapacity * sizeof(HeapDataType));
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}
	php->a[php->size] = x;
	php->size++;
	AdjustUp(php->a, php->size - 1);
}

//向上调整算法
void AdjustUp(HeapDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		//小根堆
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
//交换数据
void Swap(HeapDataType* p1, HeapDataType* p2)
{
	HeapDataType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

测试一下向上调整算法和插入数据的功能：

int main()
{
	Heap hp;
	HeapInit(&hp);
	int a[] = { 65,100,70,32,50,60 };
	int sz = sizeof(a) / sizeof(a[0]);
	int i = 0;
	for (i = 0; i < sz; i++)
	{
		HeapPush(&hp, a[i]);
	}
	return 0;
}

 

删除堆顶的数据

挪动覆盖，不能保证还是堆——父子关系全变了

只能重新建堆

第一种方法：挪动覆盖删除堆顶元素，重新建堆

但是这种方法的代价太大了 

第二种方法：首尾数据交换，再删除，再调堆

这种方法就需要用到一种算法——向下调整算法

 

向下调整算法的前提是：左子树和右子树是大堆/小堆

//向下调整算法
//这边写int* 而不写HeapDataType* 是有意为之的 为以后堆排序作准备
void AdjustDown(int* a, int n, int parent)
{
	//默认左孩子小
	int child = parent * 2 + 1;
	while (child < n)//孩子在数组范围内
	{
		//选出左右孩子中小/大的那一个
		//有可能假设错了
		//左孩子不存在，一定没有右孩子——完全二叉树
		//左孩子存在，有可能没有右孩子
		if ( child + 1 < n && a[child + 1] < a[child])
		//	右孩子存在			右孩子<左孩子
		//不能这么写 if (la[child + 1] < a[chid] && child + 1 < n )
		//这样写会有越界的风险 因为是先访问了数组中的元素 再去比较右孩子是否存在
		{
			++child;
		}
		//child就是小的那个孩子
		//不关心到底是左孩子还是右孩子 小根堆：和小的孩子比较就可以了
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			child = parent * 2 + 1;//默认又算的是左孩子
		}
		else
		{
			break;
		}

	}
}
//删除堆顶数据
void HeapPop(Heap* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	Swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;
	AdjustDown(php->a, php->size, 0);
}

判空

//判空
bool HeapEmpty(Heap* php)
{
	assert(php);
	if (php->size == 0)
	{
		return true;
	}
	else
	{
		return false;
	}
}

堆顶元素和元素个数 

//堆顶元素
HeapDataType HeapTop(Heap* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	return php->a[0];
}
//元素个数
int HeapSize(Heap* php)
{
	assert(php);
	return php->size;
}

堆的销毁

//堆的销毁
void HeapDestroy(Heap* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->size = 0;
	php->capacity = 0;
}

测试一下上述功能：

#include"heap.h"
int main()
{
	Heap hp;
	HeapInit(&hp);
	int a[] = { 65,100,70,32,50,60 };
	int sz = sizeof(a) / sizeof(a[0]);
	int i = 0;
	for (i = 0; i < sz; i++)
	{
		HeapPush(&hp, a[i]);
	}
	while (!HeapEmpty(&hp))
	{
		int top = HeapTop(&hp);
		printf("%d\n", top);
		HeapPop(&hp);
	}
	return 0;
}

 

 模拟实现堆的源代码如下：

heap.c的内容：

#include"heap.h"
//堆的初始化
void HeapInit(Heap* php)
{
    assert(php);
    php->a = NULL;
    php->size = 0;
    php->capacity = 0;
}
//堆的销毁
void HeapDestroy(Heap* php)
{
    assert(php);
    free(php->a);
    php->a = NULL;
    php->size = 0;
    php->capacity = 0;
}
//交换数据
void Swap(HeapDataType* p1, HeapDataType* p2)
{
    HeapDataType tmp = *p1;
    *p1 = *p2;
    *p2 = tmp;
}
//向上调整算法
void AdjustUp(HeapDataType* a, int child)
{
    int parent = (child - 1) / 2;
    while (child > 0)
    {
        //小根堆
        if (a[child] < a[parent])
        {
            Swap(&a[child], &a[parent]);
            child = parent;
            parent = (child - 1) / 2;
        }
        else
        {
            break;
        }
    }
}
//插入数据
void HeapPush(Heap* php, HeapDataType x)
{
    assert(php);
    //扩容
    if (php->size == php->capacity)
    {
        int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
        HeapDataType* tmp = (HeapDataType*)realloc(php->a, newcapacity * sizeof(HeapDataType));
        if (tmp == NULL)
        {
            perror("realloc fail");
            return;
        }
        php->a = tmp;
        php->capacity = newcapacity;
    }
    php->a[php->size] = x;
    php->size++;
    AdjustUp(php->a, php->size - 1);
}
//向下调整算法
//这边写int* 而不写HeapDataType* 是有意为之的 为以后堆排序作准备
void AdjustDown(int* a, int n, int parent)
{
    //默认左孩子小
    int child = parent * 2 + 1;
    while (child < n)//孩子在数组范围内
    {
        //选出左右孩子中小/大的那一个
        //有可能假设错了
        //左孩子不存在，一定没有右孩子——完全二叉树
        //左孩子存在，有可能没有右孩子
        if ( child + 1 < n && a[child + 1] < a[child])
        //    右孩子存在            右孩子<左孩子
        //不能这么写 if (la[child + 1] < a[chid] && child + 1 < n )
        //这样写会有越界的风险 因为是先访问了数组中的元素 再去比较右孩子是否存在
        {
            ++child;
        }
        //child就是小的那个孩子
        //不关心到底是左孩子还是右孩子 小根堆：和小的孩子比较就可以了
        if (a[child] < a[parent])
        {
            Swap(&a[child], &a[parent]);
            child = parent;
            child = parent * 2 + 1;//默认又算的是左孩子
        }
        else
        {
            break;
        }

    }
}
//判空
bool HeapEmpty(Heap* php)
{
    assert(php);
    if (php->size == 0)
    {
        return true;
    }
    else
    {
        return false;
    }
}
//删除堆顶数据
void HeapPop(Heap* php)
{
    assert(php);
    assert(!HeapEmpty(php));
    Swap(&php->a[0], &php->a[php->size - 1]);
    php->size--;
    AdjustDown(php->a, php->size, 0);
}
//堆顶元素
HeapDataType HeapTop(Heap* php)
{
    assert(php);
    assert(!HeapEmpty(php));
    return php->a[0];
}
//元素个数
int HeapSize(Heap* php)
{
    assert(php);
    return php->size;
}

heap.h的内容：

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int HeapDataType;
typedef struct Heap
{
    HeapDataType* a;
    int size;
    int capacity;
}Heap;
//堆的初始化
void HeapInit(Heap* php);
//堆的销毁
void HeapDestroy(Heap* php);
//插入数据
void HeapPush(Heap* php, HeapDataType x);
//向上调整算法
void AdjustUp(HeapDataType* a, int child);
//删除堆顶数据
void HeapPop(Heap* php);
//向下调整算法
void AdjustDown(int* a, int n, int parent);
//判空
bool HeapEmpty(Heap* php);
//堆顶元素
HeapDataType HeapTop(Heap* php);
//元素个数
int HeapSize(Heap* php);

好啦，小雅兰今天的学习内容就到这里啦，下篇博客小雅兰将继续分享二叉树的相关知识点，敬请期待！！！

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/682719.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

MES系统是什么？它如何帮助企业提高生产效率？

MES系统是什么？它如何帮助企业提高生产效率？

随着制造业的发展&#xff0c;越来越多的企业开始使用全面的制造执行系统&#xff08;MES&#xff09;来管理其生产过程。那么&#xff0c;MES系统到底是什么呢&#xff1f;它又是如何帮助企业提高生产效率的呢&#xff1f;本文将为大家详细介绍。 一、MES系统的概念 MES系统是…
阅读更多...
Leetcode 剑指 Offer II 032. 有效的变位词

Leetcode 剑指 Offer II 032. 有效的变位词

题目难度: 简单 原题链接 今天继续更新 Leetcode 的剑指 Offer&#xff08;专项突击版&#xff09;系列, 大家在公众号 算法精选 里回复 剑指offer2 就能看到该系列当前连载的所有文章了, 记得关注哦~ 题目描述 给定两个字符串 s 和 t &#xff0c;编写一个函数来判断它们是不…
阅读更多...
基于物联网技术的智能配电室综合监控系统设计与产品选型

基于物联网技术的智能配电室综合监控系统设计与产品选型

摘要&#xff1a;配电室是电力系统的重要基础设施&#xff0c;可以保障供配电系统的安全稳定运行。但是&#xff0c;配电室数量多、部署分散、管理复杂&#xff0c;人工现场巡检管理方式费时费工、错误率高&#xff0c;如果发生故障隐患&#xff0c;往往无法及时发现。针对配电…
阅读更多...
Sparse Fuse Dense: 向高质量的深度补全3D检测迈进

Sparse Fuse Dense: 向高质量的深度补全3D检测迈进

点云的稀疏性&#xff1a;在远距离和遮挡区域提供的信息较差&#xff0c;导致难以生成精确的3D边界框。 出现了多模态融合。 图像和点云的不同表示方式使得它们难以融合&#xff0c;导致性能不佳。 论文提出了一种新颖的多模态框架SFD&#xff08;Sparse Fuse Dense&#xf…
阅读更多...
二层交换机工作原理与MAC地址介绍

二层交换机工作原理与MAC地址介绍

目录 MAC地址介绍 MAC地址的组成 MAC地址分类 MAC地址的作用 二层交换机介绍 MAC地址表的定义 MAC地址表项类型 二层交换机对数据帧的处理动作 MAC地址介绍 MAC地址&#xff08;Media Access Control Address)&#xff0c;直译为媒体存取控制位地址 MAC地址的组成 MA…
阅读更多...
华为OD机试真题（Java），图片整理（100%通过+复盘思路）

华为OD机试真题（Java），图片整理（100%通过+复盘思路）

一、题目描述 Lily上课时使用字母数字图片教小朋友们学习英语单词&#xff0c;每次都需要把这些图片按照大小&#xff08;ASCII码值从小到大&#xff09;排列收好。请大家给Lily帮忙&#xff0c;通过代码解决。 Lily使用的图片使用字符"A"到"Z"、“a"…
阅读更多...
JMeter 环境配置

JMeter 环境配置

目录 前言&#xff1a; 一、 JDK安装 二、 安装JMeter 三、 安装插件 前言&#xff1a; JMeter是一款功能强大的性能测试工具&#xff0c;用于模拟多种负载条件下的应用程序行为&#xff0c;环境配置是jmeter学习的第一步&#xff0c;每次换电脑就得重新配置&#xff0c;为…
阅读更多...
Spark RDD dataframe嘿嘿

Spark RDD dataframe嘿嘿

RDD&#xff08;Resilient Distributed Datasets&#xff09;可扩展的弹性分布式数据集&#xff0c;RDD是spark最基本的数据抽象&#xff0c;RDD表示一个只读、分区且不变的数据集合&#xff0c;是一种分布式的内存抽象&#xff0c;与分布式共享内存&#xff08;Distributed Sh…
阅读更多...
面试题：希尔排序是一种稳定排序吗？

面试题：希尔排序是一种稳定排序吗？

面试题&#xff1a;希尔排序是一种稳定排序吗&#xff1f; 对于算法的稳定性&#xff0c;有这样一个记忆技巧&#xff0c;不稳定排序是"快些选队"&#xff0c;对应于快速排序/希尔排序/选择排序/堆排序。希尔排序也名列其中&#xff0c;因此也是一种不稳定排序&…
阅读更多...
CODESYS 数组类型变量(ARRAY)使用介绍

CODESYS 数组类型变量(ARRAY)使用介绍

博途PLC数组类型变量使用介绍请参看下面文章博客： 博途1200/1500PLC上升沿下降沿指令编程应用技巧(bool数组)_博途上升沿指令_RXXW_Dor的博客-CSDN博客博途PLC的下降沿和上升沿指令，在控制系统编程时经常会使用。和SMARTS7-200有所不同，遵循IEC-6113标准提供的上升沿下降沿…
阅读更多...
【初识C语言（6）】指针+结构体

【初识C语言（6）】指针+结构体

文章目录 1. 指针1.1 内存1.2 指针变量的大小 2. 结构体 1. 指针 想要学好指针&#xff0c;首先必须要先了解内存。 1.1 内存 内存介绍 内存是电脑上特别重要的存储器&#xff0c;计算机中程序的运行都是在内存中进行的 。 所以为了有效的使用内存&#xff0c;就把内存划分…
阅读更多...
​LeetCode解法汇总1401. 圆和矩形是否有重叠

​LeetCode解法汇总1401. 圆和矩形是否有重叠

目录链接&#xff1a; 力扣编程题-解法汇总_分享记录-CSDN博客 GitHub同步刷题项目&#xff1a; https://github.com/September26/java-algorithms 原题链接&#xff1a;力扣 描述&#xff1a; 给你一个以 (radius, xCenter, yCenter) 表示的圆和一个与坐标轴平行的矩形 (x1…
阅读更多...
第三方医药数据供应商有哪些？--数据业务介绍

第三方医药数据供应商有哪些？--数据业务介绍

第三方医药数据供应商主要是为医药企业、健康机构、学术研究、药物研发等提供医药相关数据的收集、整理、分析和应用服务。随着医药市场的需求衍生了许多各高垂直领域的医药数据供应商&#xff0c;这也导致了大家对医药数据供应商涉及领域认识的片面性。 故本文重点介绍各医药…
阅读更多...
SpringBoot 如何使用 YourKit 进行性能调优

SpringBoot 如何使用 YourKit 进行性能调优

SpringBoot 如何使用 YourKit 进行性能调优 前言 在应用程序的开发过程中&#xff0c;性能调优是一个重要的环节。如果应用程序的性能不佳&#xff0c;可能会影响用户的体验&#xff0c;甚至导致系统崩溃。而在 Spring Boot 应用程序中&#xff0c;我们可以使用 YourKit 来进…
阅读更多...
同比增长超500% 威睿公司三电产品4月装机量增势迅猛

同比增长超500% 威睿公司三电产品4月装机量增势迅猛

近期&#xff0c;2023年4月装机量数据全新出炉&#xff0c;威睿公司在电驱动系统、电机控制器、驱动电机、PACK、BMS等多个装机量榜单中跻身前十位&#xff0c;同比增长均超过100%。其中电驱动系统装机量位列第六位&#xff0c;电驱动系统、电机控制器、驱动电机装机量同比增长…
阅读更多...
本地离线安装Selenium

本地离线安装Selenium

1、去官网&#xff08;下载地址:https://pypi.org/project/selenium/#history&#xff09;去下载selenium版本 2、此处建议大家下载selenium的3.0的版本&#xff0c;我给的地址可以让你直接进入选择历史版本的跳转页面。 3、往下拉&#xff0c;到3左右的版本&#xff0c;点击版…
阅读更多...
【Docker】Docker Compose详解

【Docker】Docker Compose详解

文章目录 概述Docker Compose介绍Docker Compose安装一、下载Docker Compose&#xff1a;二、授权三、快速上手第一步、创建python服务第二步&#xff0c;创建 Dockerfile第三步&#xff0c;使用 Compose 文件定义一个服务第四步、使用 Compose 编译启动应用 Docker Compose常用…
阅读更多...
【JUC进阶】04. 无锁CAS

【JUC进阶】04. 无锁CAS

目录 1、前言 2、CAS概念和原理 2.1、什么是CAS 2.2、CAS原理 2.3、工作方式 2.4、无锁CAS优势 3、unsafe类 4、ABA问题 4.1、什么是ABA问题 4.2、解决ABA问题 4.2.1、版本号机制 4.2.2、AtomicStampReference 5、CAS适用的场景 1、前言 无锁的Compare and Swap&…
阅读更多...
libevent（9）通过libevent实时监听文件的更新

libevent（9）通过libevent实时监听文件的更新

这里我们利用libevent监听centos系统上的login日志文件&#xff0c;文件路径&#xff1a;/var/log/secure。&#xff08;ubuntu下是"/var/log/auth.log"&#xff09; 代码如下 test_file.cpp&#xff1a; #include <iostream> #include <thread> #inclu…
阅读更多...
数据迁移ETL工具分享

数据迁移ETL工具分享

1.概述 ETL(是Extract-Transform-Load的缩写&#xff0c;即数据抽取、转换、装载的过程)&#xff0c;对于企业应用来说&#xff0c;我们经常会遇到各种数据的处理、转换、迁移的场景。 我汇总了一些目前市面上比较常用的ETL数据迁移工具&#xff0c;希望对你会有所帮助。 2. …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023