目录
- 前言
- 使用深度可分离卷积
- 普通卷积的计算参数量
- 深度可分离卷积分为两个步骤:深度卷积和逐点卷积
- 使用多个缩放因子
- 使用 Swish 激活函数
前言
高效的神经网络主要通过:1. 减少参数数量;2. 量化参数,减少每个参数占用内存
目前的研究总结来看分为两个方向:
一是对训练好的复杂模型进行压缩得到小模型;
二是直接设计小模型并进行训练。(EfficientNet属于这类)
深度可分离卷积中的深度卷积不改变输入通道数,再由逐点卷积的方式,将多通道信息相融合。
ResNet和EfficientNet都是非常经典和高效的卷积神经网络,它们各有特点,适用于不同的场景和任务。ResNet通过残差连接解决梯度消失问题,可以构建非常深的神经网络,适用于图像分类、目标检测和语义分割等任务;
EfficientNet通过复合缩放方法优化网络结构,可以在保持高准确性的同时减少计算量和内存占用,适用于移动设备和嵌入式设备等资源受限的场景。
使用深度可分离卷积
传统的卷积操作在处理通道和空间信息时是耦合的,而深度可分离卷积可以分别对通道和空间信息进行处理,从而减少了计算量和参数量。具体来说,深度可分离卷积分为两个步骤:深度卷积和逐点卷积。深度卷积使用一个卷积核对每个通道进行卷积,而逐点卷积则使用 1x1 的卷积核对每个通道的输出进行组合。由于逐点卷积的计算量比传统的卷积操作小得多,因此深度可分离卷积可以大大减少计算量和参数量。
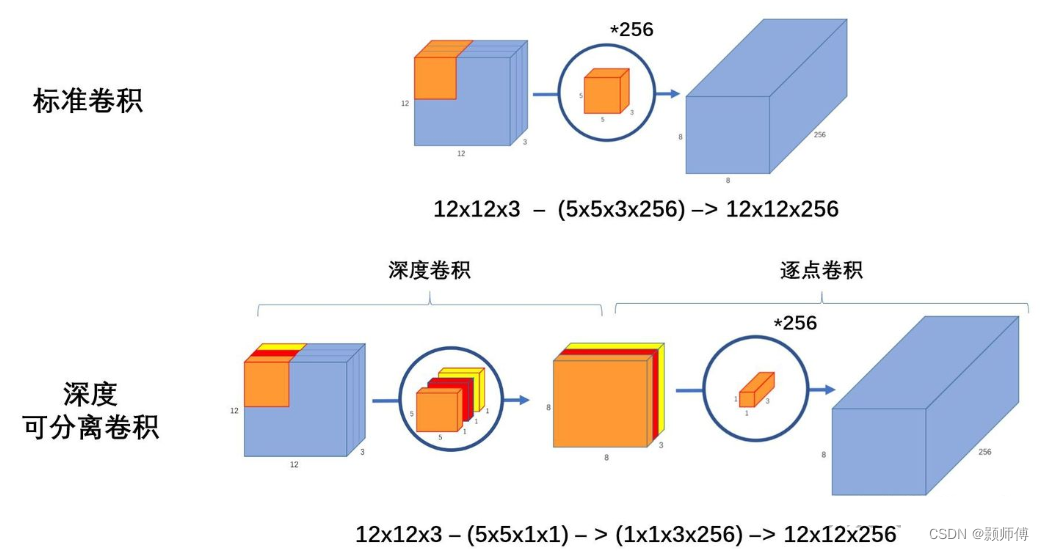
普通卷积的计算参数量
传统卷积的参数计算可以简单地理解为卷积核中所有参数的数量。具体地,假设输入张量的大小为 H × W × C H \times W \times C H×W×C,输出张量的大小为 H ′ × W ′ × C ′ H' \times W' \times C' H′×W′×C′,卷积核的大小为 K × K K \times K K×K,传统卷积的参数计算如下:
对于每个输出通道 c ′ c' c′,都要使用一个独立的卷积核来卷积输入张量的所有通道。因此,对于每个输出通道 c ′ c' c′,卷积核中的参数数量为 K × K × C K \times K \times C K×K×C。
由于每个输出通道都有一个独立的卷积核,因此对于所有输出通道的卷积核,参数数量为 K × K × C × C ′ K \times K \times C \times C' K×K×C×C′。
需要加上偏置的参数数量,假设每个输出通道都有一个独立的偏置,那么偏置的参数数量为 C ′ C' C′。
因此,传统卷积的总参数数量为
K
×
K
×
C
×
C
′
+
C
′
K \times K \times C \times C' + C'
K×K×C×C′+C′。
例如,假设输入张量大小为
224
×
224
×
3
224 \times 224 \times 3
224×224×3,输出张量大小为
112
×
112
×
32
112 \times 112 \times 32
112×112×32,卷积核大小为
3
×
3
3 \times 3
3×3。那么传统卷积的总参数数量为
3
×
3
×
3
×
32
+
32
=
896
3 \times 3 \times 3 \times 32 + 32 = 896
3×3×3×32+32=896。
需要注意的是,传统卷积的参数数量随着输入和输出张量的大小、卷积核的大小和输出通道数的增加而增加,这可能导致在深层网络中出现参数量过大的问题。因此,深度可分离卷积是一种有效的替代方法,可以减少参数数量和计算量。
深度可分离卷积分为两个步骤:深度卷积和逐点卷积
深度也就是指:channel这一维度。
深度卷积操作是将每个通道单独处理,以减少计算量和参数量。具体来说,对于一个输入张量,深度卷积操作首先对每个通道应用一个单独的卷积核,然后将每个通道的结果相加得到输出张量。由于每个通道使用单独的卷积核,因此每个卷积核的参数量大大减少。
逐点卷积操作是用一个 1x1 的卷积核对每个通道的输出进行组合。逐点卷积可以将不同通道的信息进行组合,从而增强特征表示能力。
深度可分离卷积的参数数目比传统卷积要少得多,这是深度可分离卷积被广泛应用于移动设备和嵌入式设备等资源受限的环境中的主要原因之一。下面以一个简单的例子说明深度可分离卷积的参数数目:
假设输入张量的大小为
H
×
W
×
C
H \times W \times C
H×W×C,输出张量的大小为
H
′
×
W
′
×
C
′
H' \times W' \times C'
H′×W′×C′,卷积核的大小为
K
×
K
K \times K
K×K,深度可分离卷积的参数数目可以分为两个部分:深度卷积的参数数目和逐点卷积的参数数目。
深度卷积的参数数目。深度卷积使用一个 K × K × 1 K \times K \times 1 K×K×1 的卷积核对每个通道进行卷积,因此每个卷积核的参数数目为 K × K × 1 = K 2 K \times K \times 1=K^2 K×K×1=K2,所有卷积核的参数数目为 K 2 × C ′ K^2 \times C' K2×C′,即深度卷积的参数数目为 K 2 × C ′ K^2 \times C' K2×C′。
逐点卷积的参数数目。逐点卷积使用一个
1
×
1
1 \times 1
1×1 的卷积核对每个通道的输出进行组合,因此每个卷积核的参数数目为
1
×
1
×
C
=
C
1 \times 1 \times C= C
1×1×C=C,所有卷积核的参数数目为
C
×
C
′
C \times C'
C×C′,即逐点卷积的参数数目为
C
×
C
′
C \times C'
C×C′。
因此,深度可分离卷积的总参数数目为
K
2
×
C
′
+
C
×
C
′
K^2 \times C' + C \times C'
K2×C′+C×C′,相比传统卷积,深度可分离卷积的参数数目大大减少,这使得深度可分离卷积能够在相同的计算资源下获得更好的性能。
使用多个缩放因子
EfficientNet 使用了一种称为 Compound Scaling 的方法,对网络的深度、宽度和分辨率进行缩放,以适应不同的计算资源和应用场景。具体来说,Compound Scaling 包括三个因子:深度因子、宽度因子和分辨率因子。深度因子控制网络的深度,宽度因子控制每层的通道数,分辨率因子控制输入图像的分辨率。通过调整这些因子,可以在不同的计算资源下获得更好的性能。
通过增加输入图像的分辨率来提升网络的表达能力和视觉感知能力。
这三个方面的缩放是相互关联的,因此需要进行联合优化。具体来说,对于每个缩放因子
ϕ
\phi
ϕ,可以使用以下公式来计算网络的深度
d
d
d、宽度
w
w
w 和分辨率
r
r
r:
d
=
α
ϕ
w
=
β
ϕ
r
=
γ
ϕ
\begin{aligned} d &= \alpha^\phi \ w &= \beta^\phi \ r &= \gamma^\phi \ \end{aligned}
d=αϕ w=βϕ r=γϕ
其中,
α
\alpha
α、
β
\beta
β 和
γ
\gamma
γ 是网络的基础深度、宽度和分辨率,
ϕ
\phi
ϕ 是缩放因子,可以根据计算资源的限制来确定。通过联合优化这三个方面的缩放因子,可以获得更加高效的网络结构。
需要注意的是,EfficientNet 使用了一种复合扩张系数(Compound Coefficient)的方法,将每个卷积层的扩张系数设置为一个复合系数,可以在不增加计算量的情况下增加网络的表达能力。具体来说,复合扩张系数由两个部分组成:一个固定的基础扩张系数
θ
\theta
θ 和一个可调整的复合因子
ϕ
\phi
ϕ。每个卷积层的扩张系数可以表示为
α
β
ϕ
\alpha\beta^\phi
αβϕ,其中
α
\alpha
α 是网络基础通道数,
β
\beta
β 是复合系数中的基础系数,
ϕ
\phi
ϕ 是可调整的复合因子。通过联合优化复合扩张系数和缩放因子,可以获得更加高效的网络结构。
总之,Compound Scaling 方法能够同时对网络深度、宽度和分辨率进行优化,通过联合优化复合扩张系数和缩放因子,可以获得更加高效的网络结构,从而获得更好的性能和计算效率。
使用 Swish 激活函数
EfficientNet 使用了 Swish 激活函数代替了传统的 ReLU 激活函数。Swish 激活函数的公式为 f(x) = x * sigmoid(x),它可以更好地平衡计算速度和准确率。Swish 激活函数在计算量方面与 ReLU 相当,但在准确率方面更好。
总之,EfficientNet 的优化方法主要包括使用深度可分离卷积、使用多个缩放因子和使用 Swish 激活函数。这些优化方法的目的是减少计算量和参数量,提高计算效率和准确率,并使网络更加适用于现代计算机视觉应用。