算法流程

先学决策树，再学随机森林，最后才来到xgboost。本以为如此平滑地过渡过来，会容易一些，没想到还是这么艰难。零零散散花了3周多的时间，看了好多文章的解释和阐述，才勉强get到xgboost的算法原理。

这其中，有两个参考来源，我个人比较推荐：一个是文字，一个是视频。

此处直接给出xgboost的算法流程图，方便我们直观认识xgboost。针对一个训练集，xgboost首先使用CART树训练得到一个模型，这样针对每个样本都会产生一个偏差值；然后将样本偏差值作为新的训练集，继续使用CART树训练得到一个新模型；以此重复，直至达到某个退出条件为止。

最终的xgboost模型就是将上述所有模型进行加和。假设一共有M个模型，每个模型的输出被定义为$f_i$，那么xgboost模型的最终输出${\hat{y}}_i$为
$${\hat{y}}_i=\sum _{i=1}^M{f}_i(x_i)$$

显然，xgboost和随机森林一样，也是多个模型的集成，但是它们之间还存在诸多不同。用专业术语来描述的话，那就是xgboost是Boosting的方式，核心特点在于降低偏差，逻辑是串行的；而随机森林是Bagging的方式，核心特点在于降低方差，逻辑是并行的。

弄清楚了算法流程，我们还需要关注流程中的细节。需要搞明白的事情有两个：（1）什么是CART树？（2）CART树模型如何得到？

CART树

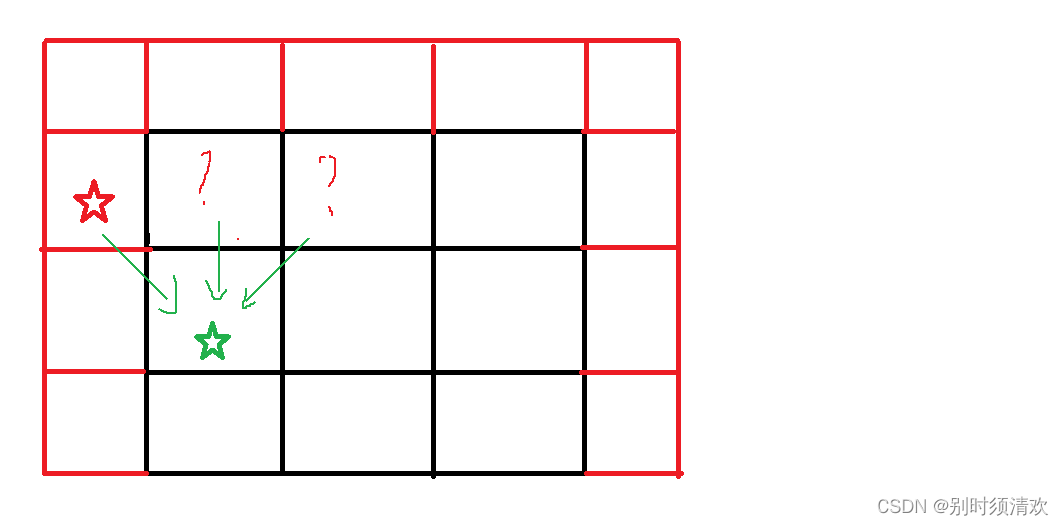
简单理解，CART树首先是一个树；在此基础上，每个叶子节点$j$都会被赋予一个节点值$w_j$。

假设第$i$个样本$x_i$和第$j$个节点之间的映射关系为
$$j=q(x_i)$$
以下图为例：$q(x_1)=2,q(x_2)=1,q(x_3)=2$。

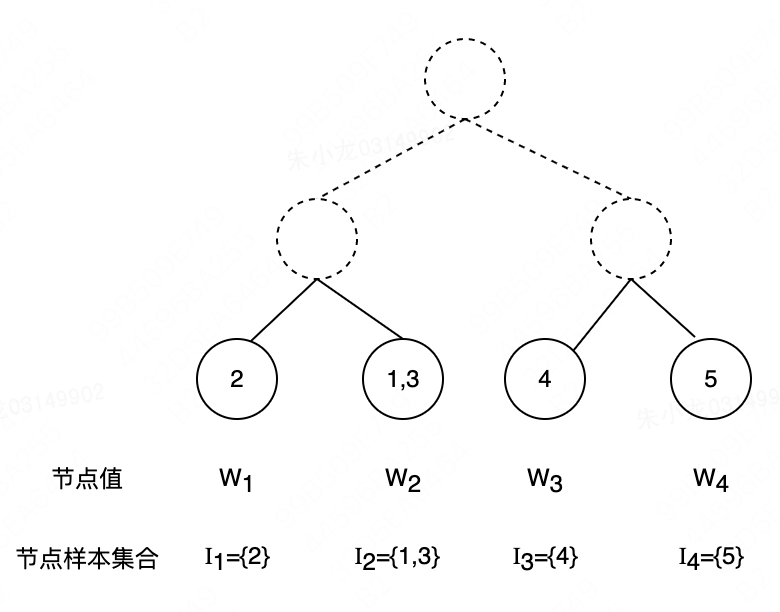
那么第$i$个样本的节点值为
$$w_{q(x_i)}$$
反过来说的话，第$j$个节点的样本集合$I_j$可以表达为
I j = { x i ∣ q ( x i ) = j } I_j= \{x_i|q(x_i)=j \} Ij​={xi​∣q(xi​)=j}
还是以上图为例： I 1 = { 2 } , I 2 = { 1 , 3 } I_1=\{2\}, I_2=\{1,3\} I1​={2},I2​={1,3}。

从CART树的概念上，我们很容易发现，确定一颗CART树需要两类数据：树结构和节点值。接下来，我们先研究清楚，树结构固定时的最佳节点值优化策略；在此基础上，再返回来尝试确定最佳的树结构。

最佳节点值

当树结构固定后，每个样本落入的节点随即确定。此时，定义如下的目标函数来衡量xgboost对整体样本的误差
$$\text{obj}=\sum _{i=1}^{n}l(y_i,{\hat{y}}_i^{(M)})+\sum _{m=1}^M\Omega (f_m)$$
其中，第一项的含义是样本自身误差，$n$表示样本数量，$l(\cdot )$是衡量样本误差的函数，如MSE等，$y_i$为第$i$个样本的真值，${\hat{y}}_i^{(M)}$为第$i$个样本的预测值；第二项是正则项，正则项之前在线性模型优化：岭回归和Lasso回归中用到过，主要目的是降低过拟合风险，此处的目标同样是降低过拟合的风险。

第二项简单，先处理一下
$$\sum _{m=1}^M\Omega (f_m)=\sum _{m=1}^{M-1}\Omega (f_m)+\Omega (f_M)$$
从算法流程可知，CART树是一颗一颗建立起来的，当我们要优化第$M$颗树的时候，前$M-1$颗树已经完成了计算，即这些树的正则项值已经确定，所以我们在优化时可以不考虑；对于第$M$颗树，$\Omega$被定义为
$$\Omega (f_M)=\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2$$
该定义可以如此理解：一方面，$T$值大，说明树的深度比较深，过拟合的概率就会变高，所以使用$\gamma$进行惩罚；另一方面，$w$值大，说明该树在整个模型中会占据较大的比重，即预测结果主要依赖该树，此时过拟合风险也会变高，所以需要再使用$\lambda$进行惩罚。

现在回到第一项。有了第二项的具体表达式后，如果再给定$l(\cdot )$的表达式，看起来好像可以直接通过梯度求导得到极值。但实际上该方式是不可行的。这主要是因为$\hat{y}$是通过树模型得到的，所以该值并不连续，所以不可导。

既然如此，我们就需要其它的解决方案。好在，因为前$M-1$颗CART树已经确定，所以只需要关注第$M$颗树的节点值即可，所以第一项可以转化为
$$\sum _{i=1}^{n}l(y_i,{\hat{y}}_i^{(M)})=\sum _{j=1}^T\sum _{i\in I_j}l(y_i,{\hat{y}}_i^{(M)})$$
该转化的价值在于将误差的统计逻辑从样本的加和转化为节点的加和，这样就可以和$\Omega$使用相同的变量，便于表达式的合并操作。

为了处理该项，我们将对其进行泰勒展开，并保留至二阶项。

先回顾泰勒公式
$$f(x+\delta x)=f(x)+f^{\prime }(x)\delta x+\frac{1}{2}{f}^{\prime \prime }(x)\delta x^2$$
此处把${\hat{y}}_i^{(M-1)}$定义为$x$，那么$\delta x$就是$w_j$，我们照葫芦画瓢进行泰勒展开
$$l(y_i,{\hat{y}}_i^{(M)})=l(y_i,{\hat{y}}_i^{(M-1)}+w_j)=l(y_i,{\hat{y}}_i^{(M-1)})+l^{\prime }(y_i,{\hat{y}}_i^{(M-1)})w_j+\frac{1}{2}{l}^{\prime \prime }(y_i,{\hat{y}}_i^{(M-1)})w_j^2$$
第一个为常量，也可以不考虑。令$g_i=l^{\prime }(y_i,{\hat{y}}_i^{(M-1)})$，$h_i=l^{\prime \prime }(y_i,{\hat{y}}_i^{(M-1)})$
。

总的目标函数变为

$$\text{obj}=\sum _{j=1}^T\sum _{i\in I_j}[g_i{w}_j+\frac{1}{2}{h}_i{w}_j^2]+\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2$$
由于$w_j$和$i$无关，所以可以调整为
$$\text{obj}=\sum _{j=1}^T[w_j\sum _{i\in I_j}{g}_i+\frac{1}{2}{w}_j^2\sum _{i\in I_j}{h}_i]+\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2$$
合并$w_j^2$项，得到
$$\text{obj}=\sum _{j=1}^T[w_j\sum _{i\in I_j}{g}_i+\frac{1}{2}{w}_j^2(\lambda +\sum _{i\in I_j}{h}_i)]+\gamma T$$

令$G_j={\sum }_{i\in I_j}{g}_i$，$H_j={\sum }_{i\in I_j}{h}_i$，上式可以简化为
$$\text{obj}=\sum _{j=1}^T[w_j{G}_j+\frac{1}{2}{w}_j^2(\lambda +H_j)]+\gamma T$$
这是个二元一次表达式，最优解为
$$w_j^{\ast }=-\frac{G_j}{\lambda +H_j}$$
对应的最优目标函数值为
$${\text{obj}}^{\ast }=-\frac{1}{2}\sum _{j=1}^T\frac{G_j^2}{\lambda +H_j}+\gamma T$$

此处还需要描述一下$g_i$和$h_i$具体是如何计算的。举个例子，假设我们正在优化第11棵CART树，也就是说前10棵 CART树已经确定了。这10棵树对样本($x_i,y_i=1$)的预测值是$y_i=-1$，假设我们现在是做分类，我们的损失函数是
$$L(\theta )=\sum _i{y}_{i}ln(1+e^{-{\hat{y}}_i})+(1-y_i)ln(1+e^{{\hat{y}}_i})$$
由于$y_i=1$，损失函数变为
$$L(\theta )=ln(1+e^{-{\hat{y}}_i})$$
求梯度，结果为
$$\frac{e^{-{\hat{y}}_i}}{1-e^{-{\hat{y}}_i}}$$
将${\hat{y}}_i=-1$带入梯度表达式，便得到$g_{11}=-0.27$。

针对梯度表达式继续求导，得到二阶导数表达式后，再带入${\hat{y}}_i$的值，便可得到$h_{11}$。

再理解一下$w_j^{\ast }$。假设节点处只有一个样本，此时
$$w_j^{\ast }=(\frac{1}{\lambda +h_j})(-g_j)$$
$-g_j$代表的是负梯度方向，即目标函数值下降最快的方向，这是符合我们认知的；$\frac{1}{\lambda +h_j}$可以看作是学习率，如果$h_j$值大，表明梯度变化比较大，即微小的扰动都会带来目标函数的极大变化，此时应该让学习率小一些，所以也是符合我们的认知的。

综上，只要树结构确定了，那么就可以通过以上的方法得到每个节点的最优值$w_i$，从而使得目标函数值最小。现在，我们只剩最佳树结构了。

最佳树结构

为了确定最佳的树结构，本节介绍一种常用的方法：贪心算法。

如下图所示。针对当前节点，有A、B和C三个样本，可以计算得到该节点处的最优目标函数值为
$${\text{obj}}_0=\gamma -\frac{1}{2}\frac{(G_A+G_B+G_C{)}^2}{H_A+H_B+H_C+\lambda }$$

尝试将该节点拆分，假设可能出现三种情况，[A, BC]、[C, AB]和[B, AC]，对应的最优目标函数值分别为
$${\text{obj}}_1=2\gamma -\frac{1}{2}\frac{G_A^2}{H_A+\lambda }-\frac{1}{2}\frac{(G_B+G_C{)}^2}{H_B+H_C+\lambda }$$
$${\text{obj}}_2=2\gamma -\frac{1}{2}\frac{(G_A+G_B{)}^2}{H_A+H_B+\lambda }-\frac{1}{2}\frac{(G_C{)}^2}{H_C+\lambda }$$
$${\text{obj}}_3=2\gamma -\frac{1}{2}\frac{(G_A+G_C{)}^2}{H_A+H_C+\lambda }-\frac{1}{2}\frac{(G_B{)}^2}{H_B+\lambda }$$

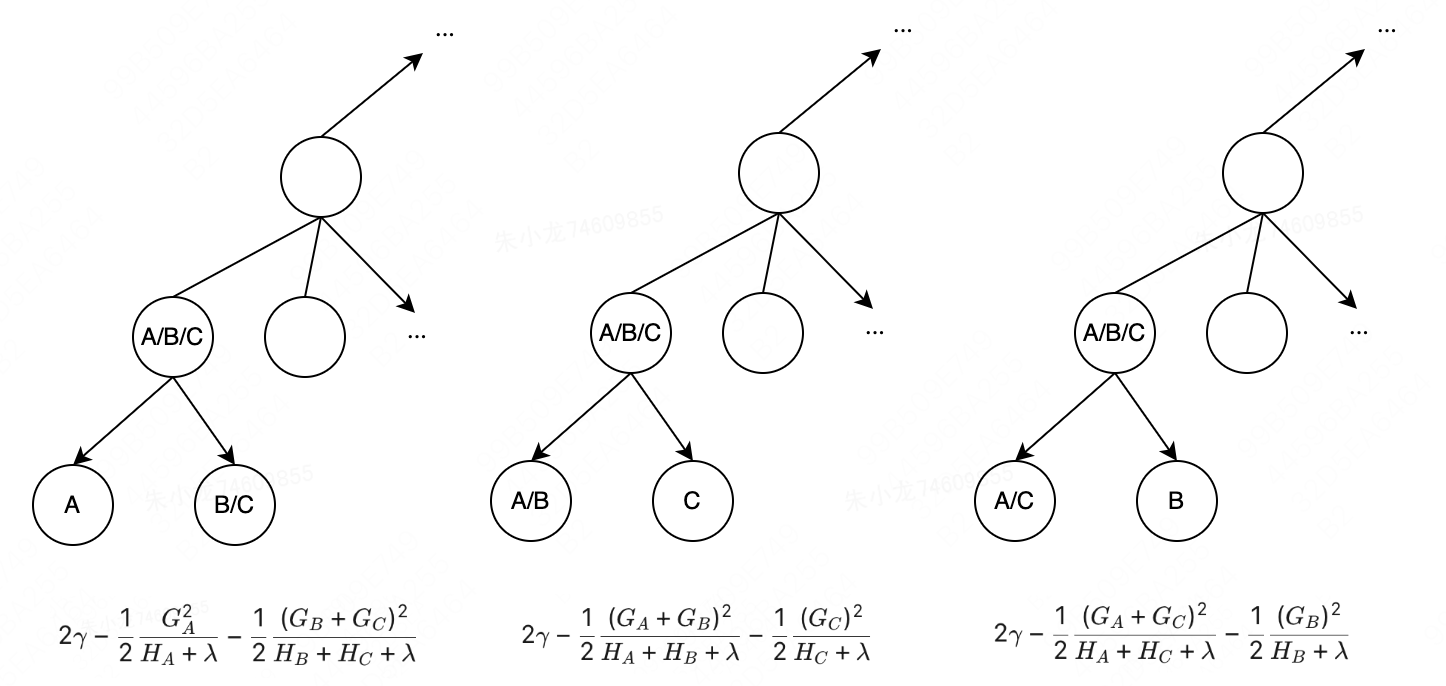
分别计算3种情况下的目标函数变化值，即：${\text{obj}}_1-{\text{obj}}_0$、${\text{obj}}_2-{\text{obj}}_0$和${\text{obj}}_3-{\text{obj}}_0$。然后取最大的变化值所对应的拆分结果作为下次该节点的最佳拆分方式。

所以确定最佳树结构的流程是：
从树的深度为0开始：
（1）对每个叶节点枚举所有的可用特征；
（2）针对每个特征，把属于该节点的训练样本根据该特征值进行升序排列，通过以上的贪心逻辑来决定该特征的最佳拆分点，并记录该特征的拆分收益；
（3）选择收益最大的特征作为拆分特征，用该特征的最佳拆分点作为拆分位置，在该节点上拆分出左右两个新的叶节点，并为每个新节点关联对应的样本集；
（4）回到第1步，重复执行直到满足特定条件为止；

至此，总算是搞明白了xgboost的算法原理。