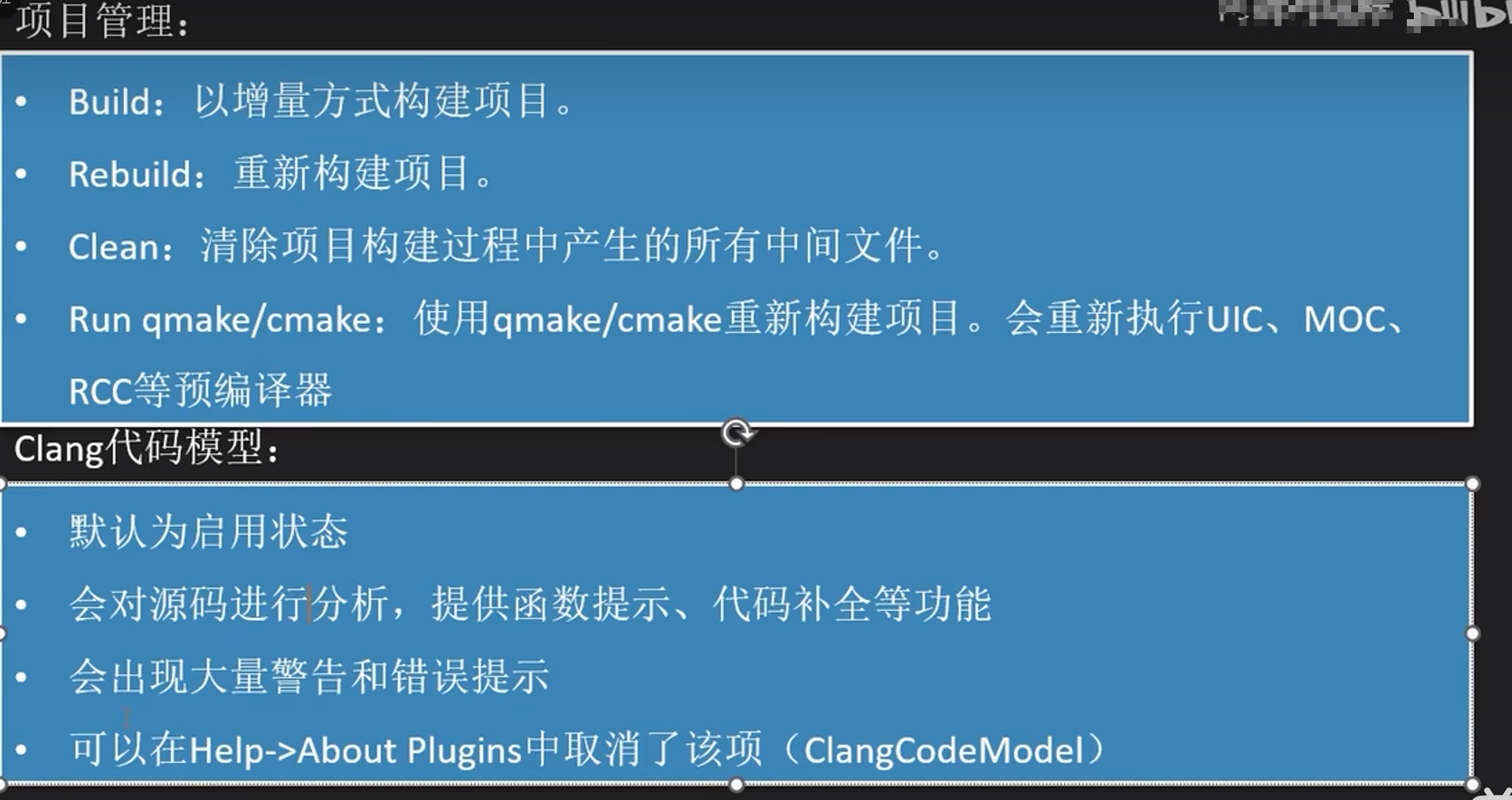
本专栏是网易云课堂人工智能课程《神经网络与深度学习》的学习笔记，视频由网易云课堂与 deeplearning.ai 联合出品，主讲人是吴恩达 Andrew Ng 教授。刚兴趣的网友可以观看网易云课堂的视频进行深入学习，视频的链接如下：

https://mooc.study.163.com/course/2001281002

也欢迎对神经网络与深度学习感兴趣的网友一起交流 ~

目录

1 二分类问题

2 Logistic 回归

2.1 Logistic 回归模型

2.2 Logistic 回归损失函数

2.3 Logistic 回归代价函数

---

1 二分类问题

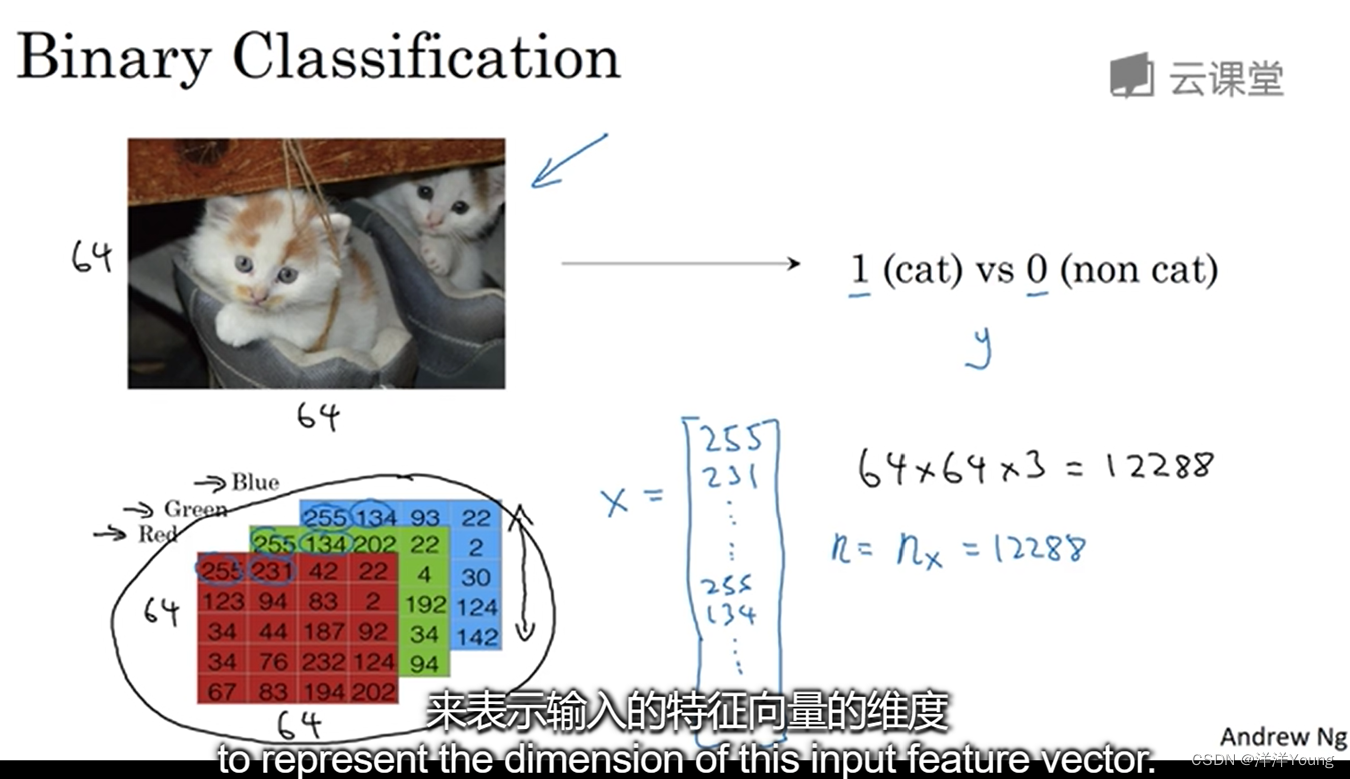
        假如你有一张图片（以高维向量的形式）作为输入 ，你希望计算机识别它。如果是猫，输出 1；如果不是，则输出 0。这里的输出  只能取 0 或 1，所以这个问题属于二分类问题。

2 Logistic 回归

2.1 Logistic 回归模型

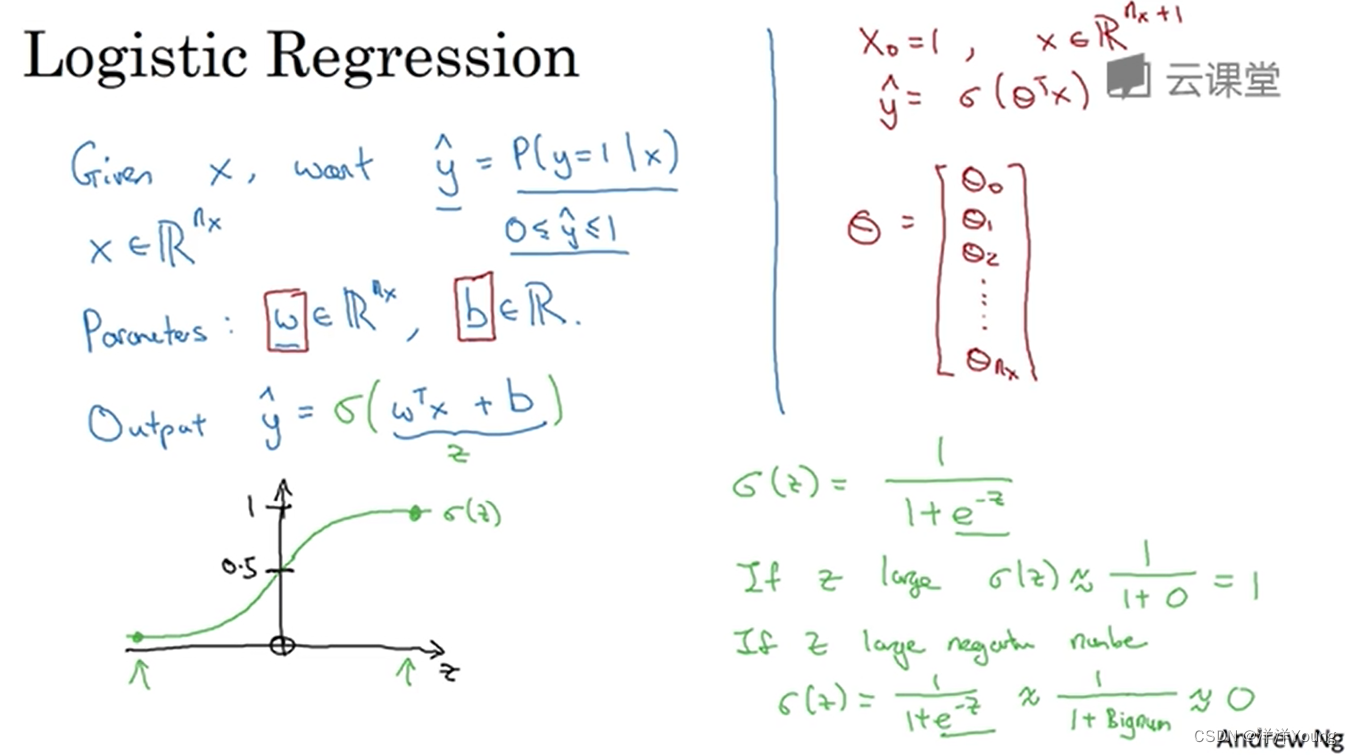
        Logistic 回归是一个用于二分类问题的算法。在 Logistic 回归模型中，输出  的含义是在给定  的条件下，输出  的概率，即

模型输出值  等于 sigmoid 函数作用在  上。

2.2 Logistic 回归损失函数

        当你实现 Logistic 回归模型时，你要做的工作是让神经网络学习参数  和 ，这需要定义损失函数。

        损失函数（Loss function）也叫错误函数（Error function)，用于衡量模型了预测值  和实际值  的差别。

        先来看  应满足的要求：

        （i）如果 ，那么 ；

        （ii）如果 ，那么 .

函数

 

可以满足上述要求，两边取对数得

        定义 Logistic 模型的损失函数为

当我们训练神经网络时，最小化损失函数 ，等价于最大化 .

        如果 ，根据（i）可知，最大化  等价于最大化 ，又因为 ，所以最大化  其实是希望  尽可能地接近 1.

        如果 ，根据（ii）可知，最大化  等价于最小化 ，同理因为 ，所以最小化  其实是希望  尽可能地接近 0.

2.3 Logistic 回归代价函数

        损失函数计算了模型在单个训练样本上的错误程度，代价函数（Cost function）则计算模型在整个训练集上的错误程度。

        对于 m 个训练样本，假设所有训练样本独立同分布，则 m 个样本的联合概率为

 两边取对数，得

定义 Logistic 模型的代价函数为