什么是微分冲击Derivative Kick
引入微分,就是为了减少超调量的,但是根据PID的经典公式
就看微分部分
在PID刚开始时,误差值肯定是存在的,但是PID启动的瞬间,这个dt是很小的,这就导致是一个很大的值,因为误差是在瞬间变化的,那误差的微分当然就比较大,那输出Output就会有一个比较大的波动。同理,在重新设置目标值的时候也会有同样的情况,这种显现就叫微分冲击(Derivative Kick)。
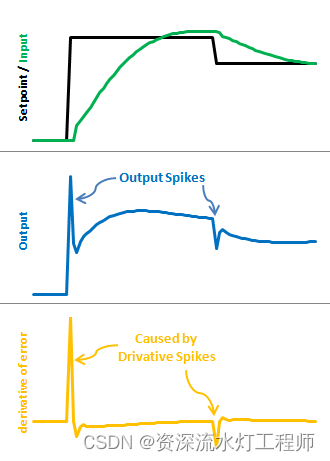
这个微分冲击对控制系统肯定是不友好的,比如车速调节系统,会导致车速的顿挫。肯定有方法来解决这个问题。
解决方案
还是从本质入手,误差的微分dErr是怎么得来的
如果目标值Setpoint是一个固定不变的,dSetpoint = 0;
这就说明,只要目标值Setpoint不变化,偏差(Error)的导数等于输入(Input)的负导数。
那管你目标值变不变,都把输入的负倒数等价于误差的倒数,问题解决了,再也没有Setpoint来影响输出了。
实现代码如下:
/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double errSum, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
void Compute()
{
unsigned long now = millis();
int timeChange = (now - lastTime);
if(timeChange>=SampleTime)
{
/*Compute all the working error variables*/
double error = Setpoint - Input;
errSum += error;
double dInput = (Input - lastInput);
/*Compute PID Output*/
Output = kp * error + ki * errSum - kd * dInput;
/*Remember some variables for next time*/
lastInput = Input;
lastTime = now;
}
}
void SetTunings(double Kp, double Ki, double Kd)
{
double SampleTimeInSec = ((double)SampleTime)/1000;
kp = Kp;
ki = Ki * SampleTimeInSec;
kd = Kd / SampleTimeInSec;
}
void SetSampleTime(int NewSampleTime)
{
if (NewSampleTime > 0)
{
double ratio = (double)NewSampleTime
/ (double)SampleTime;
ki *= ratio;
kd /= ratio;
SampleTime = (unsigned long)NewSampleTime;
}
}这里的修改相当容易。在前面一章代码的基础上,将+dError替代为-dInput。那记录的变量也就是上一次的输入lastInput,而不是上一次的误差lastError。
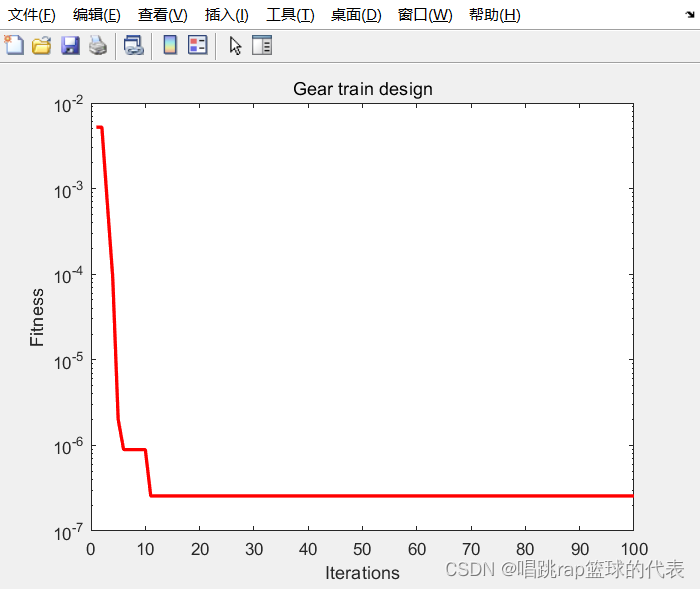
结果

结果就如上图所示,突变没有了。即使有的控制系统对这个突变不敏感,但是就改这么点代码能完美的解决这个隐患,何乐不为呢,写代码还是尽量追求完美吧,少给自己和他人埋雷。