当矩阵中存在着重复元素时，为了节省空间会采用压缩算法，关键在于原矩阵空间与压缩后数据结构的对应；

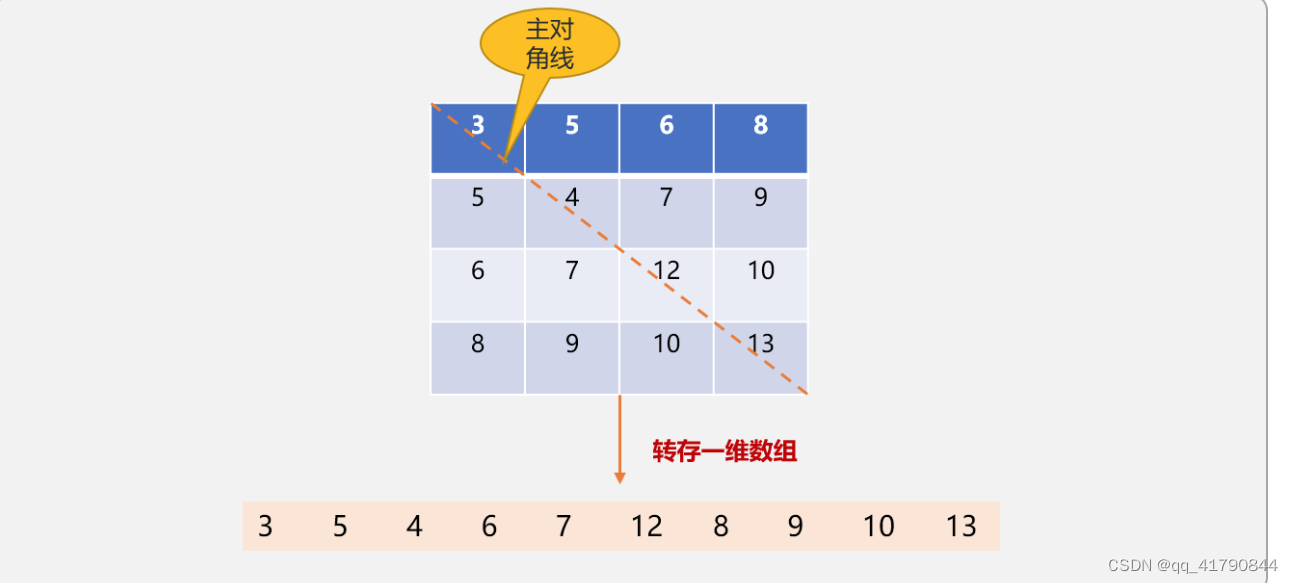
1.对称压缩：数据沿对角线对称的情况；

将矩阵压缩为一维数组，数组的长度是：

对于num[n][n];

zipNum.size()=(n+1)*n/2;

元素的对应：这是直接针对二维数组来说的，一般的矩阵起始是从1开始的，那会是i(i-1)/2+j-1;

 

 代码如下：

int main() 
{


	int nums[4][4] = { {3,5,6,8},{5,4,7,9},{6,7,12,10},{8,9,10,13} };

zipNums.size()=4*(4+1)/2=10;
	int zipNums[10] = {0};


	for (int i = 0; i < 4; i++)
		{
		for (int j = 0; j < 4; j++)
			{
			if (i >= j) { zipNums[i * (i +1) / 2 + j] = nums[i][j]; }
			else		{ zipNums[j * (j + 1) / 2 + i] = nums[i][j]; }
			}

		
		}

	for (int i = 0; i < 10; i++)
	{
		cout << zipNums[i] << " ";
	}

return 0;
}

这是对称矩阵压缩；

上三角矩阵：与对称矩阵一样，但需要一个额外的空间存放常数；

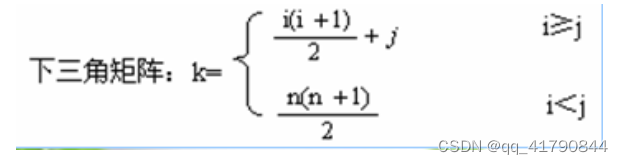
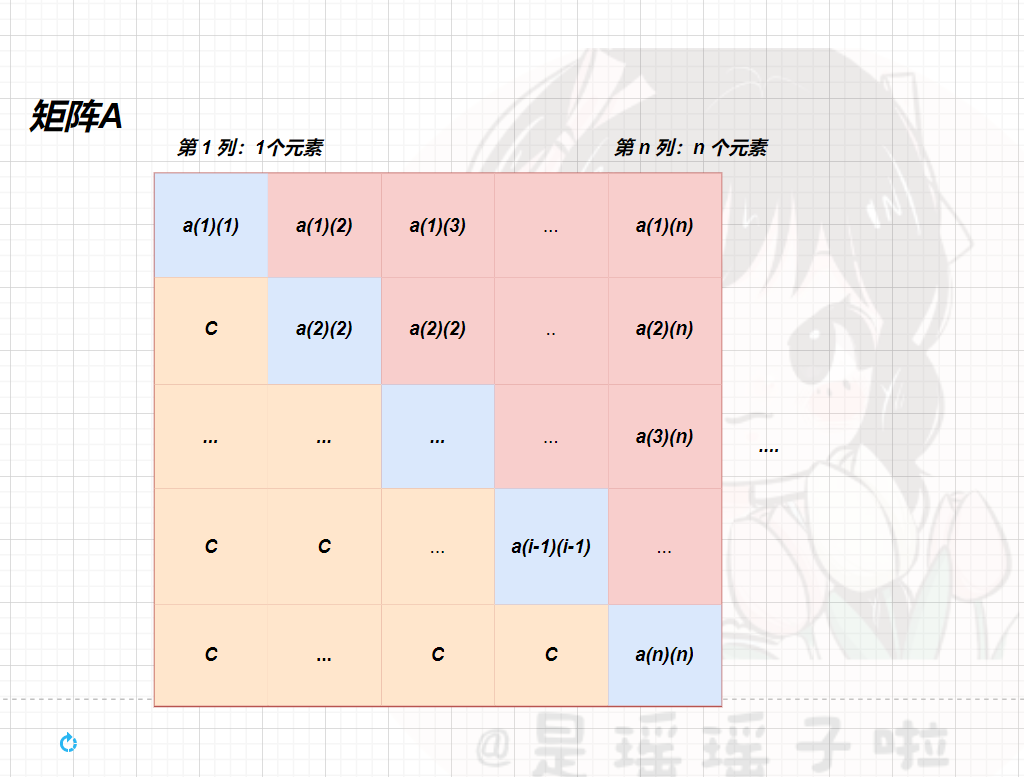
下三角矩阵：与上三角相反；

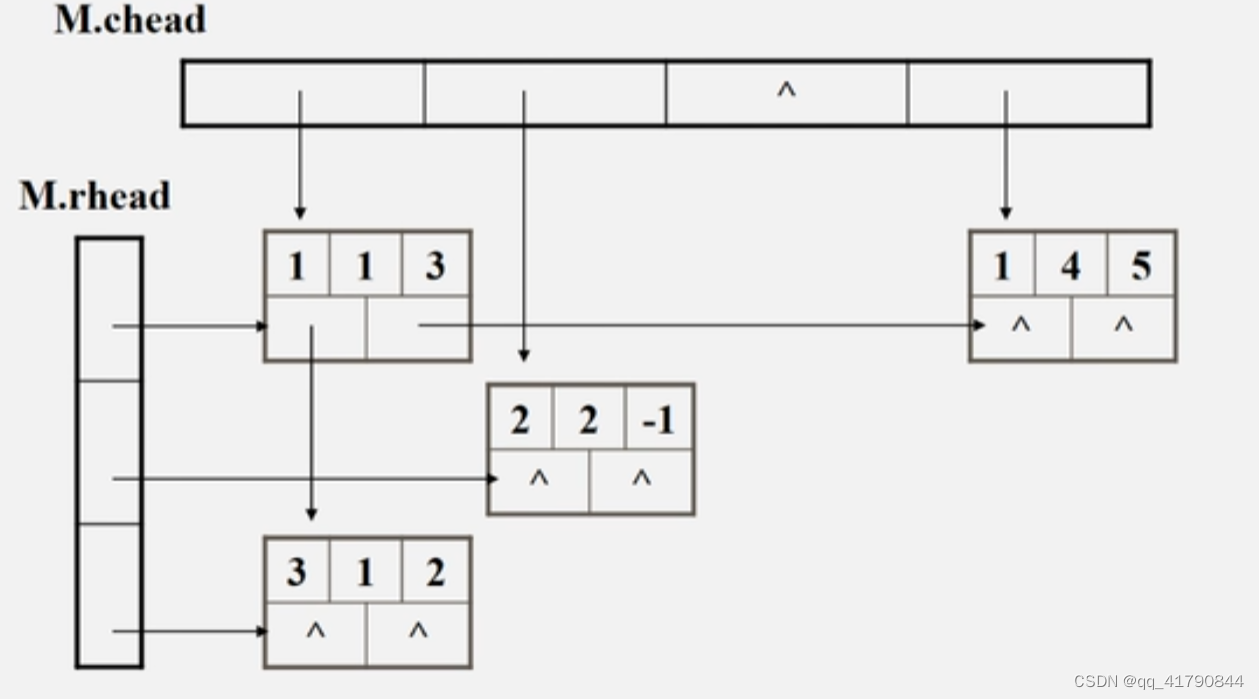
稀疏压缩（难点）：

如果一个矩阵中的有效元素很少，则应该使用稀疏压缩算法；稀疏矩阵也可以采用十字链表来压缩；

C++ 特殊矩阵的压缩存储算法_问题 a: 特殊的方阵 c++_一枚大果壳的博客-CSDN博客

【数据结构】特殊矩阵的压缩存储|保姆级详解+图解_数据结构图的压缩存储_是瑶瑶子啦的博客-CSDN博客各种特殊矩阵的压缩存储_日事日毕_日清日高的博客-CSDN博客

三元组法即用结构数组记录数的行列号和值；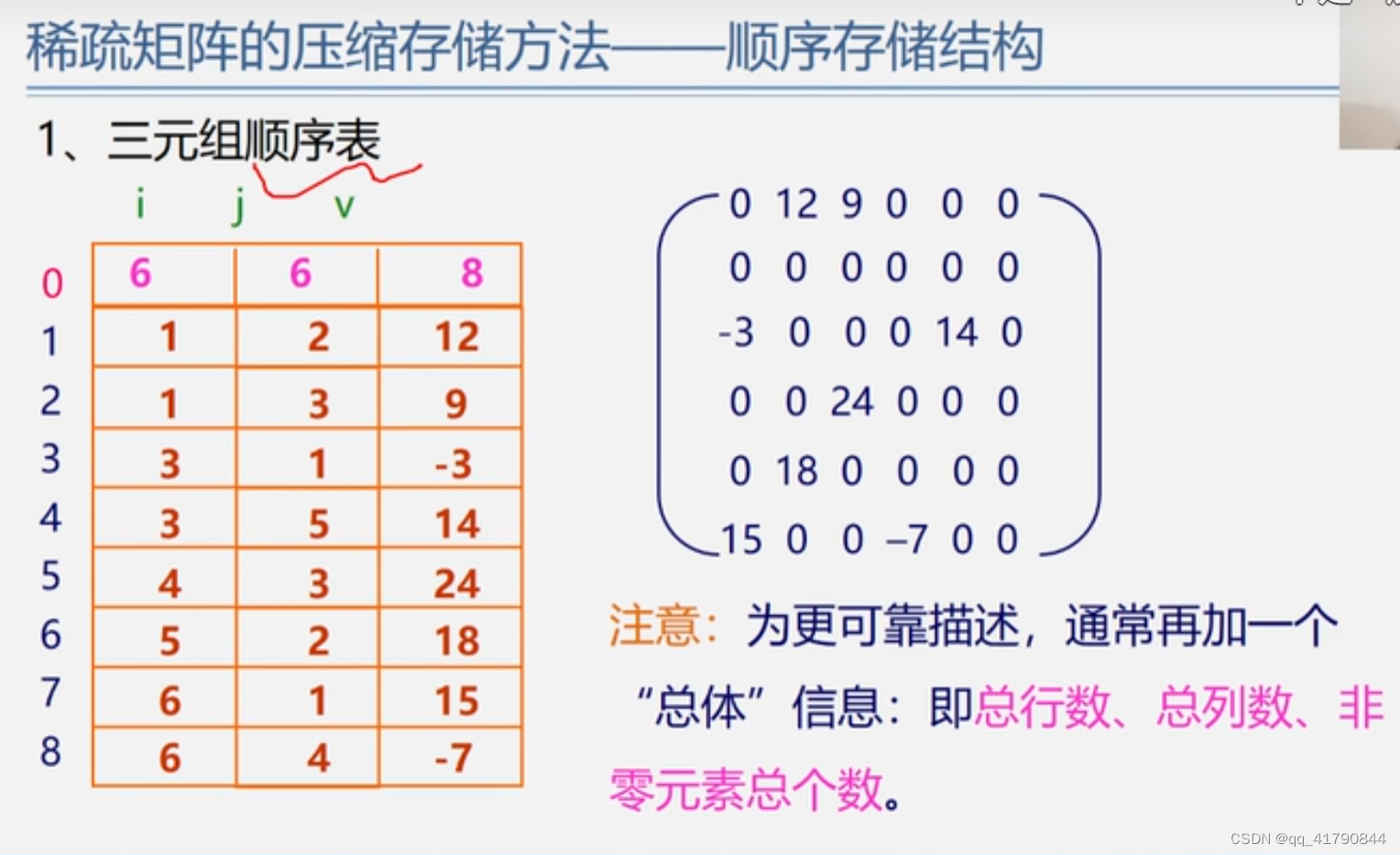

#define Max 30

struct Three{

int row;
int col;
int val
}Three,Th[Max];

三元组法：具有顺序存储的缺点，即查找，添加，删除非常困难，因此对于要变动的稀疏矩阵可以采用十字链表进行存储：采用十字链表时需要额外的两个行列的头节点数组来来方便查找；也可以用一个数组来记录，这个数组的结构元素要具有两个指针；

#define MAX 10

struct LinkedList
{

int row;
int col;
int val;

LinkList*next_row;
LinkList*next_col;

};

typedef struct DOUBLE_XN
{

LinkList*head_row;
LinkList*head*col;
}XN,XML[MAX];

XML[MAX]就是头节点数组；

typedef struct ONE_XN
{

LinkList*head;
//LinkList*head*col;
}XN,XM[MAX];


XM[MAX]就是单一的数组；