leetcode188. 买卖股票的最佳时机 IV

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iv

题目描述

给定一个整数数组 prices ，它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格，和一个整型 k 。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说，你最多可以买 k 次，卖 k 次。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1：
输入：k = 2, prices = [2,4,1]
输出：2
解释：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

示例 2：
输入：k = 2, prices = [3,2,6,5,0,3]
输出：7
解释：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。

提示：
0 <= k <= 100
0 <= prices.length <= 1000
0 <= prices[i] <= 1000

动态规划

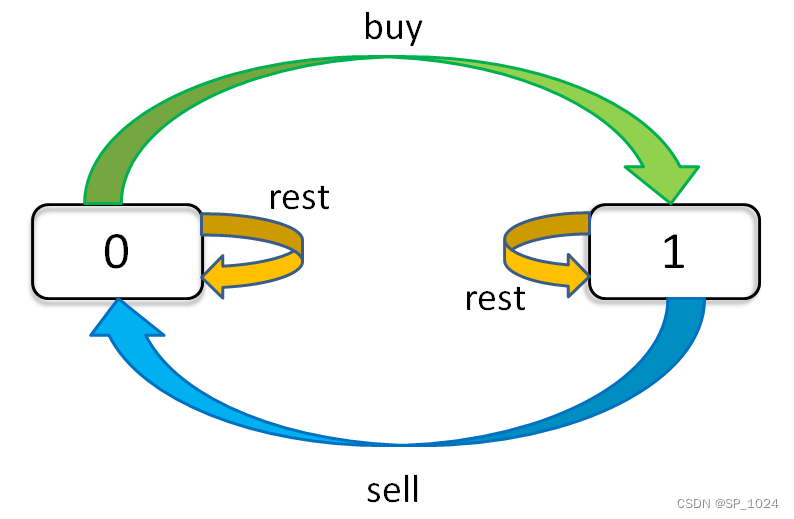
我们先找出这里面变化的状态。第一个是天数。第二个是允许交易的次数。第三个是当前持有的状态。持有的状态只有两个，持有和没持有，我们用0代表没持有，1代表持有。然后我们用一个三维数组来组织这个dp表。

dp[i][k][0 or 1]
0 <= i <= n - 1, 1 <= k <= K
n 为天数，大 K 为交易数的上限，0 和 1 代表是否持有股票。
此问题共 n × K × 2 种状态，全部穷举就能搞定。

持有和没持有的状态是互相转换的，

根据这个转换的关系，我们写下状态转移方程：

dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
解释：今天我没有持有股票，有两种可能，我从这两种可能中求最大利润：
1、我昨天就没有持有，且截至昨天最大交易次数限制为 k；然后我今天选择 rest，所以我今天还是没有持有，最大交易次数限制依然为 k。
2、我昨天持有股票，且截至昨天最大交易次数限制为 k；但是今天我 sell 了，所以我今天没有持有股票了，最大交易次数限制依然为 k。

2.dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
解释：今天我持有着股票，最大交易次数限制为 k，那么对于昨天来说，有两种可能，我从这两种可能中求最大利润：
1、我昨天就持有着股票，且截至昨天最大交易次数限制为 k；然后今天选择 rest，所以我今天还持有着股票，最大交易次数限制依然为 k。
2、我昨天本没有持有，且截至昨天最大交易次数限制为 k - 1；但今天我选择 buy，所以今天我就持有股票了，最大交易次数限制为 k。

根据上面总结，我们得出状态转移方程：
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])

代码演示

 int maxProfit(int max_k, int[] prices) {
         int N = prices.length;
     
        int[][][]dp = new int[N][max_k + 1][2];
        for(int i = 0; i < N;i++){
            for(int j = max_k; j >= 1;j--){
                if(i == 0){
                    dp[i][j][0] = 0;
                    dp[i][j][1] = -prices[i];
                    continue;
                }
                dp[i][j][0] = Math.max(dp[i - 1][j][0],
                        dp[i - 1][j][1] + prices[i]);

                dp[i][j][1] = Math.max(dp[i - 1][j][1],
                        dp[i - 1][j - 1][0] - prices[i]);       
            }
        }

        return dp[N - 1][max_k][0];
   }