来源:投稿 作者:橡皮
编辑:学姐

论文链接:https://openreview.net/pdf?id=xzmqxHdZAwO
论文代码:尚未开源
1.背景
随着人工智能中深度视觉检测技术的快速发展,检测工业产品表面的异常/缺陷受到了前所未有的关注。生产转换是指将生产线或机器从加工一种产品转换为另一种产品。由于检测设备在生产线启动后还没有完全微调,因此这样的转换经常导致异常检测性能不令人满意。如何在转换场景中实现工业产品模型的快速训练,同时确保准确的异常检测,是实际生产过程中的一个关键问题。
AD在行业中的现状如下:
(1)就检测精度而言,在转换过程中,最先进的AD模型的性能急剧下降。当前的主流工作利用大量的训练数据作为输入来训练模型,如图(a)所示。然而,这将使数据收集具有挑战性,即使对于无监督的学习也是如此。因此,已经提出了许多以精度为代价的基于少镜头学习的方法。例如元学习,如图(b)所示。但由于设置复杂,在切换过程中无法灵活迁移到新产品,检测精度无法保证。
(2)在模型训练速度方面,当大量数据用于训练时,实际生产线上新产品的训练进度会放缓。众所周知,原始的无监督范式需要收集大量信息。尽管元学习在小样本学习中有效,如(b)所示,但仍有必要训练之前收集的大量的数据。

2.本文主要贡献
基于对以上问题的考虑,我们的目标是在生产转换过程中处理生产线的冷启动。如图(c)所示,开发了一种新的FSAD方法,称为GraphCore,该方法使用少量正常样本来实现新产品的快速训练和有竞争力的AD精度性能。一方面,通过利用少量数据,我们可以快速训练并加快异常推理的速度。另一方面,因为我们直接训练新产品样本,所以不会发生从旧产品到新产品的异常适应和迁移。
-
提出了一种用于 FSAD 的特征增强方法,以研究 CNN 生成的视觉特征的特性。
-
提出了一种新颖的异常检测模型 GraphCore,将新的 VIIF 添加到基于内存库的 AD 范例中,这可以大大减少冗余视觉特征的数量。
-
实验结果表明,所提出的 VIIF 是有效的,可以显着提高 FSAD 在 MVTec AD 和 MPDD 数据集上的性能。
3.方法简介
问题设置。 图 (c) 概述了所提出的 FSAD 问题设置的正式定义。训练过程仅包含来自特定类别的 n 个正常样本的训练集,其中 n ≤ 8。在测试时,对于给定目标类别中的正常或异常样本,异常检测模型应预测图像是否异常,如果预测结果异常,则定位异常区域。
挑战。 对于提出的 FSAD,我们尝试仅使用少量正常图像作为训练数据集来检测测试样本中的异常。主要挑战包括:(1)每个类别的训练数据集仅包含正常样本,即没有图像或像素级别的注释。 (2) 可用的训练集正态样本很少。在我们提出的设置中,训练样本少于 8 个。
动机。 在真实的工业图像数据集中,某些类别下的图像极其相似。它们中的大多数都可以通过简单的数据增强相互转换,例如螺母和螺钉。例如,旋转增强可以有效地提供新的螺旋数据集。因此,当面临上述的挑战时,我们自然倾向于通过数据扩充获取额外的数据。然后,特征存储库可以存储更多有用的特征。
4.方法细节
4.1数据增强+PATCHCORE
为了验证我们的洞察力,已将 PatchCore应用到我们的模型中。我们将 PatchCore 的增强(旋转)表示为 Aug.(R)。该架构在图2中进行了详细描述。在从 ImageNet 预训练模型中提取特征之前,会进行数据扩充(例如,旋转)。

对于PatchCore 的增强(旋转): Aug.(R)

4.2视觉等距不变特征
在4.1 中,作者启发式地证明数据增强+PatchCore 在提出的少样本异常检测上下文中优于 SOTA 模型。本质上,数据增强方法立即将正常样本的特征合并到记忆库中。换句话说,数据增强+PatchCore 提高了定位子集特征的概率,使得测试图像的异常分数可以更精确地计算。因此,作者质疑是否可以从少量正常样本中提取出不变的表征特征,并将其添加到特征记忆库中。如下图所示,作者提出了一种新的特征提取模型:视觉等距不变图神经网络 (VIIG)。所提出的模型尝试从正常样本的每个补丁中提取视觉等距不变特征 (VIIF)。如前所述,大多数工业视觉异常检测数据集都可以通过旋转、平移和翻转进行转换。因此,GNN 的同构性非常适合工业视觉异常检测

4.3图像的图(Graph)表示
下图显示了 GraphCore 的特征提取过程。具体来说,对于尺寸为 H×W×3 的普通样本图像,我们将其均匀地分成 N 个 patch。此外,每个补丁都被转换成一个特征向量 fi ∈ RD。所以我们有特征 F = [f1, f2, · · · , fN],其中 D 是特征维度,i = 1, 2, · · · , N。我们将这些特征视为无序节点 V = {v1, v2,···,vN}。对于某些每个节点 vi,我们 K 个最近邻表示 N (vi) 并为所有 vj ∈ N (vi) 添加一条从 vj 指向 vi 的边 eij。因此,每个正态样本块可以表示为图 G = (V, E)。 E指代图G的所有边。

4.4图特征处理
上图显示了所提出的视觉等距不变 GNN 的架构。具体来说,我们将特征提取设置为 GCN。通过与其邻居节点交换信息来聚合每个节点的特征。特征提取操作如下:

其中 Waggregate 和 Wupdate 表示聚合和更新操作的权重。它们都可以以端到端的方式进行优化。具体来说,每个节点的聚合操作是通过聚合相邻节点的特征来计算的:

其中h是节点特征更新函数,g是节点特征聚合特征函数。N (f li ) 表示第 l 层的 f li 的邻居节点集。具体来说,我们采用最大相对图卷积作为运算符。所以g和h定义为:

在等式 3 和 4 中,g(·) 是一个最大池化顶点特征聚合器,它聚合了节点 vi 与其所有邻居之间的特征差异。 h(·) 是具有批量归一化和 ReLU 激活的 MLP 层。
4.5 GraphCore结构
结构如下图。在训练阶段,GraphCore与Augmentation+PatchCore最显着的区别在于特征记忆库构建算法。特征构建算法同算法1:Aug.(R) memory bank。请注意,我们在没有数据增强的情况下使用视觉等距不变 GNN 作为特征提取器 P。在测试阶段,GraphCore 异常分数 s* 的计算与 Augmentation + PatchCore 中的非常相似。唯一的区别是每个正常补丁样本的特征提取方法。 GraphCore 的结构细节显示在下表21 中。


4.6 数据增强+PATCHCORE 和 GRAPHCORE 的统一视图
下图展示了 Augmentation+PatchCore 和 GraphCore 的统一视图。 Augmentation+PatchCore提示GraphCore获取等距不变特征。因此,GraphCore 可以提高定位特征子集的概率,从而可以最准确、最快速地计算出测试图像的异常分数。表 1 显示了 PatchCore、Augmentation+PatchCore 和 GraphCore 在架构细节方面的差异。


5.实验结果
GraphCore VS Augmentation+PatchCore VS RegAD 不同样本量下的结果 (K):
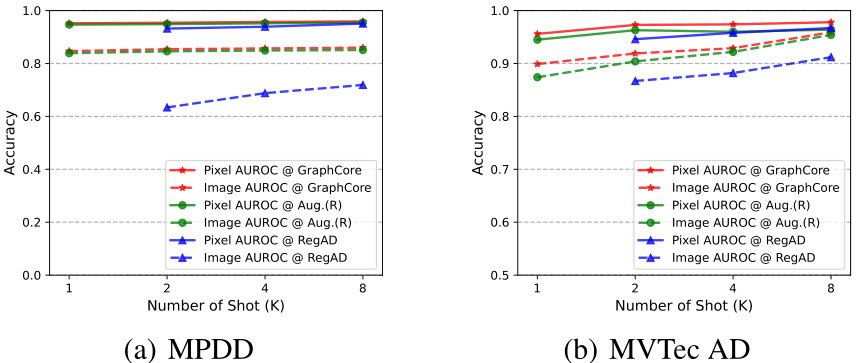
FSAD 在 MVTec AD 和 MPDD 上所有类别的平均结果。采样率为0.01,x|y分别代表图像AUROC和像素AUROC。 表现最佳的方法以粗体显示。

FSAD 在 MVTec AD 上的结果。样本量K=2,采样率为0.01,x|y分别表示图像AUROC和像素AUROC。表现最佳的方法以粗体显示。

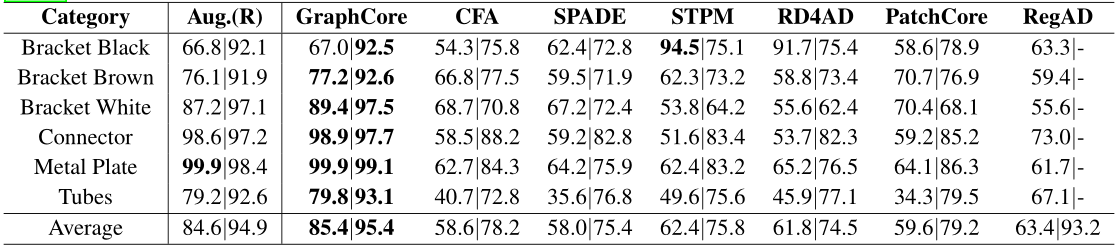
FSAD在MPDD上的结果。样本量K=2,采样率为0.01,x|y分别表示图像AUROC和像素AUROC。表现最佳的方法以粗体显示。
提出的方法在 MVTec AD 和 MPDD 上的可视化结果。

关注下方《学姐带你玩AI》🚀🚀🚀
回复“异常检测”获取全部论文PDF合集
码字不易,欢迎大家点赞评论收藏!