力扣动态规划专题（五）子序列问题 不连续子序列与连续子序列 步骤及C++实现

news2025/1/11 14:24:54

文章目录

  • 300.最长递增子序列
  • 674.最长连续递增子序列
    • 动态规划
    • 贪心算法
  • 718. 最长重复子数组
    • 二维dp数组
    • 一维dp数组
  • 1143.最长公共子序列
  • 1035.不相交的线
  • 53. 最大子序和
    • 动态规划
    • 贪心算法

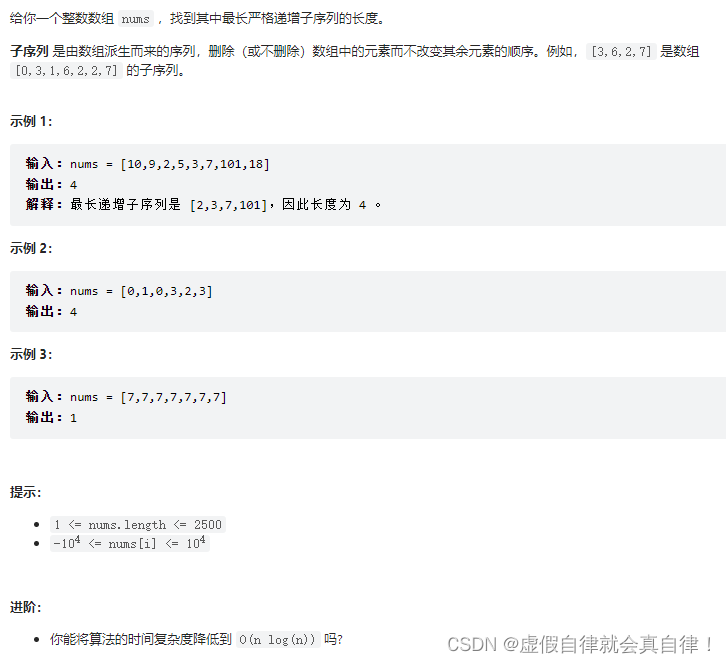
300.最长递增子序列

在这里插入图片描述

步骤

  1. 确定dp数组以及下标的含义
    dp[i]：i之前（包括i）以nums[i]结尾的最长递增子序列的长度。递增比较时，肯定要比较两个递增子序列的末尾元素，即递增子序列肯定是以末尾元素结尾的，否则比较没有意义

  2. 确定递推公式
    位置i 的最长升序子序列等于 = 位置j 的最长升序子序列 + 1 的最大值，j在[0, i-1]区间。假设dp[i]就是最长的升序子序列，那么dp[j]就是0~i-1的最长升序子序列再+1，即dp[i] = dp[j] + 1，为了取dp[j] + 1的最大值，if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
    这里不是要dp[i] 与 dp[j] + 1进行比较，而是要取dp[j] + 1的最大值。

  3. dp数组如何初始化
    每一个i，对应的最长递增子序列dp[i]起始大小至少都是1

  4. 确定遍历顺序
    dp[i] 是由0到i-1各个位置的最长递增子序列推导而来，那么遍历i一定是从前向后遍历。并且j在[0, i-1]区间，那么j既可以从前到后，也可以从后到前遍历。遍历i在外循环，遍历j在内循环

  5. 举例推导dp数组
    输入：[0,1,0,3,2]

  6. C++实现

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        if(nums.size() <= 1) return nums.size();
        vector<int> dp(nums.size(), 1);
        int result = 0;
        for(int i=1; i<nums.size(); i++)
        {
            for(int j=0; j<i; j++)
            {
                if(nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
            }
            if(dp[i] > result) result = dp[i];
        }
        return result;
    }
};

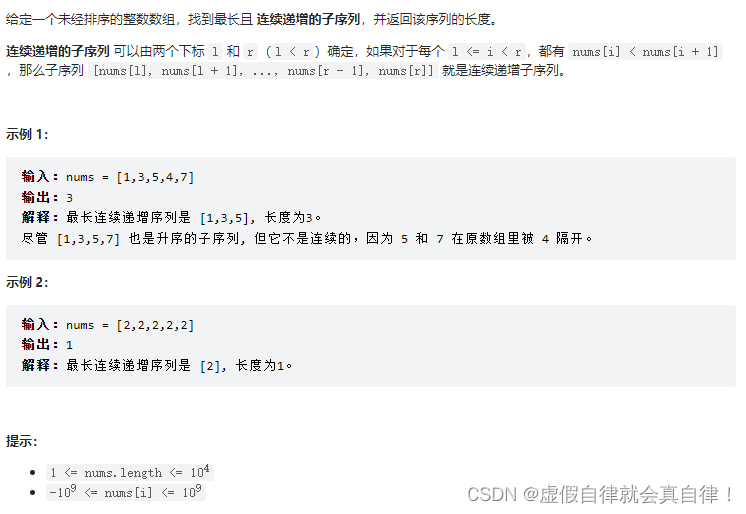
674.最长连续递增子序列

在这里插入图片描述

动态规划

步骤

相比于300.最长递增子序列最大的区别在于连续，要求的是最长连续递增序列，体现在递推公式

  1. 确定dp数组以及下标的含义
    dp[i]：以下标i为结尾的连续递增的子序列长度

  2. 确定递推公式
    如果 nums[i] > nums[i - 1]，那么以 i 为结尾的连续递增的子序列长度 = 以i - 1为结尾的连续递增的子序列长度 + 1 ，dp[i] = dp[i - 1] + 1;
    300题中比较的是nums[i]和nums[j]，而j是在[0, i-1]区间的，需要两层for循环。本题则是比较nums[i]和nums[i-1]，只需要一层for循环

  3. dp数组如何初始化
    以下标i为结尾的连续递增的子序列长度最少也应该是1

  4. 确定遍历顺序
    dp[i]依赖dp[i - 1]，从前向后遍历

  5. 举例推导dp数组
    输入nums = [1,3,5,4,7]

    dp[i]的最大值才是最终结果

  6. C++实现

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        if(nums.size() <= 1) return nums.size();
        vector<int> dp(nums.size(), 1);
        int result = 1;
        for(int i=1; i<nums.size(); i++)
        {
            if(nums[i] > nums[i-1]) dp[i] = dp[i-1] + 1;
            if(dp[i] > result) result = dp[i];
        }
        return result;
    }
};

贪心算法

只统计连续的递增序列长度，遇到nums[i] > nums[i-1]就记一次数

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        //贪心算法
        if(nums.size() == 0) return 0;
        int result = 1;
        int count = 1;
        for(int i=1; i<nums.size(); i++)
        {
            if(nums[i] > nums[i-1]) count++;
            else count = 1;
            if(count >result) result = count;
        }
        return result;
    }
};

718. 最长重复子数组

在这里插入图片描述
明确一点，子数组指的是连续子序列。

二维dp数组

步骤

  1. 确定dp数组以及下标的含义
    dp[i][j] ：以下标i - 1为结尾的nums1，和以下标j - 1为结尾的nums2，最长重复子数组长度

  2. 确定递推公式
    dp[i][j]的状态只能由dp[i - 1][j - 1]推导出来，当nums1[i - 1] 和nums2[j - 1]相等时，dp[i][j] = dp[i - 1][j - 1] + 1;，因此遍历i 和 j 都要从1开始

  3. dp数组如何初始化
    虽然dp[i][0] 和dp[0][j]没有意义，但是为了后续递推，dp[i][0] 和dp[0][j]都要初始化为0。例如，如果nums1[0]=nums2[0]，那么dp[1][1] = dp[0][0] + 1，只有dp[0][0]初始为0，才能计算dp[1][1]，并且符合递推公式。

  4. 确定遍历顺序
    遍历nums1和nums2的先后没有要求，题目要求长度最长的子数组的长度，遍历时要记录dp[i][j]的最大值

  5. C++实现

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        vector<vector<int>> dp(nums1.size()+1, vector<int>(nums2.size()+1, 0));
        int result = 0;
        for(int i=1; i<=nums1.size(); i++)
        {
            for(int j=1; j<=nums2.size(); j++)
            {
                if(nums1[i-1] == nums2[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
                if(dp[i][j] > result) result = dp[i][j];
            }
        }
        return result;
    }
};

一维dp数组

二维dp数组中，dp[i][j]都是由dp[i - 1][j - 1]推出的，那么dp[i][j]压缩为一维数组dp[j]，也就是dp[j]都是由dp[j - 1]推出的。相当于可以把上一层dp[i - 1][j]拷贝到下一层dp[i][j]来继续用，此时遍历B数组的时候，就要从后向前遍历，这样避免重复覆盖。

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        //一维dp数组
        vector<int> dp(nums2.size()+1, 0);
        int result = 0;
        for(int i=1; i<=nums1.size(); i++)
        {
            for(int j=nums2.size(); j>0; j--)
            {
                if(nums1[i-1] == nums2[j-1]) dp[j] = dp[j-1] + 1;
                else dp[j] = 0; // 注意这里不相等的时候要有赋0的操作
                if(dp[j] > result) result = dp[j];
            }
        }
        return result;
    }
};

1143.最长公共子序列

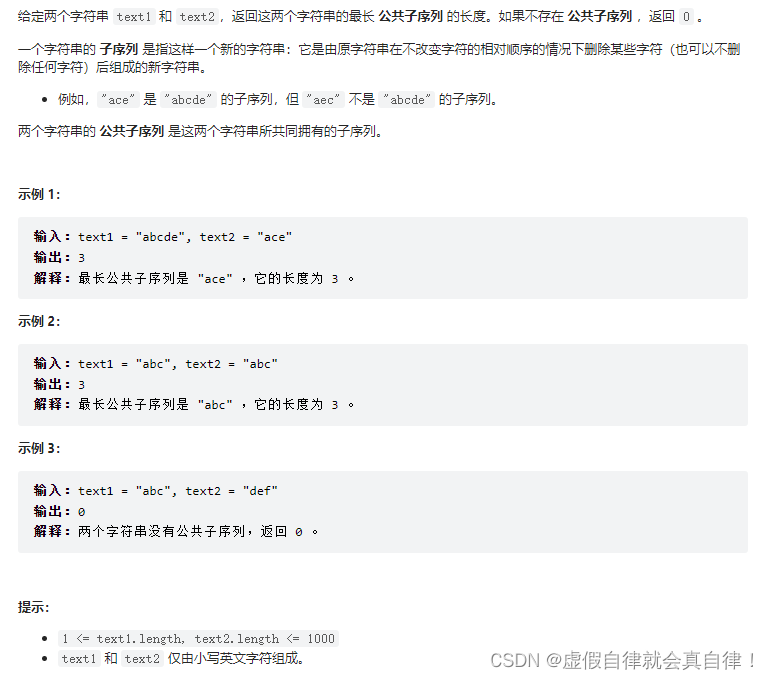
在这里插入图片描述
和718题的区别在于不要求连续，但要有相对顺序，例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。

步骤

  1. 确定dp数组以及下标的含义
    dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列的长度
    定义为长度为[0, i]的字符串text1也可以，但是实现比较复杂，需要初始化

  2. 确定递推公式

  • text1[i - 1] 与 text2[j - 1]相同，找到一个公共元素，dp[i][j] = dp[i - 1][j - 1] + 1;
  • text1[i - 1] 与 text2[j - 1]不相同，就看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的， dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);

  1. dp数组如何初始化
    test1[0, i-1]和空串的最长公共子序列是0，dp[i][0] = 0;，同理dp[0][j]=0。

  2. 确定遍历顺序
    从递推公式来看，有三个方向可以推出dp[i][j]，所以要从前向后，从上到下来遍历

  3. 举例推导dp数组
    输入：text1 = “abcde”, text2 = “ace” ，最后红框dp[text1.size()][text2.size()]为最终结果

  4. C++实现

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        vector<vector<int>> dp(text1.size()+1, vector<int>(text2.size()+1, 0));
        //从上到下 从前到后遍历
        for(int i=1; i<=text1.size(); i++)
        {
            for(int j=1; j<=text2.size(); j++)
            {
                if(text1[i-1] == text2[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
                else dp[i][j] = max(dp[i][j-1], dp[i-1][j]);
            }
        }
        return dp[text1.size()][text2.size()];
    }
};

1035.不相交的线

在这里插入图片描述

分析

绘制一些连接两个数字nums1[i] 和nums2[j] 的直线，只要nums1[i] == nums2[j]，且直线不能相交。要保证直线不相交，就不能改变数字在原始序列的位置。
换句话说，题目要求的是nums1和nums2的最长公共子序列的长度，这个公共子序列的相对顺序不能改变，也就是题1143。

步骤

  1. 确定dp数组以及下标的含义
    dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列的长度
    定义为长度为[0, i]的字符串text1也可以，但是实现比较复杂，需要初始化

  2. 确定递推公式

  • text1[i - 1] 与 text2[j - 1]相同，找到一个公共元素，dp[i][j] = dp[i - 1][j - 1] + 1;
  • text1[i - 1] 与 text2[j - 1]不相同，就看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的， dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);

  1. dp数组如何初始化
    test1[0, i-1]和空串的最长公共子序列是0，dp[i][0] = 0;，同理dp[0][j]=0。

  2. 确定遍历顺序
    从递推公式来看，有三个方向可以推出dp[i][j]，所以要从前向后，从上到下来遍历

  3. C++实现

class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        vector<vector<int>> dp(nums1.size()+1, vector<int>(nums2.size()+1, 0));
        for(int i=1; i<=nums1.size(); i++)
        {
            for(int j=1; j<=nums2.size(); j++)
            {
                if(nums1[i-1] == nums2[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
                else dp[i][j] = max(dp[i][j-1], dp[i-1][j]);
            }
        }
        return dp[nums1.size()][nums2.size()];
    }
};

53. 最大子序和

在这里插入图片描述

动态规划

步骤

  1. 确定dp数组以及下标的含义
    dp[i]：包括下标i（以nums[i]为结尾）的最大连续子序列和

  2. 确定递推公式
    dp[i]只有两个方向可以推出来

  • nums[i]加入当前连续子序列和，dp[i - 1] + nums[i]
  • 从头开始计算当前连续子序列和，nums[i]
    取最大的，dp[i] = max(dp[i - 1] + nums[i], nums[i]);

  1. dp数组如何初始化
    dp[i]依赖于dp[i - 1]的状态，dp[0]是递推公式的基础。根据dp[i]的定义，dp[0] = nums[0]

  2. 确定遍历顺序
    dp[i]依赖dp[i - 1]，从前向后遍历

  3. 举例推导dp数组
    输入：nums = [-2,1,-3,4,-1,2,1,-5,4]，最后的结果不是dp[nums.size() - 1]，而是dp[6]，和最大的连续子序列。在递推时，可以直接选出最大的dp[i]最为最终结果。

  4. C++实现

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        vector<int> dp(nums.size(), 0);
        dp[0] = nums[0];//初始化 从位置1开始遍历
        int result = dp[0];
        for(int i=1; i<nums.size(); i++)
        {
            //dp[i-1]~nums[i]的最长连续子序列  从nums[0]~nums[i]的最长连续子序列
            //去两者最大值
            dp[i] = max(dp[i-1]+nums[i], nums[i]);
            if(dp[i] > result) result = dp[i];//筛选出结果
        }
        return result;
    }
};

贪心算法

局部最优的情况下，并记录最大的“连续和”，可以推出全局最优。

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        //贪心算法
        int result = INT32_MIN;//记录最终累计和 全局解
        int count = 0;//记录当前累计和 局部最优解
        for(int i=1; i<=nums.size(); i++)
        {
            count += nums[i];//累计求和
            if(count > result) result = count;
            if(count <= 0) count = 0;//当前累计和小0
        }
        return result;
    }
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/680108.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【数据结构】单链表 创建 插入 删除 查找 完整代码

【数据结构】单链表 创建 插入 删除 查找 完整代码

3.1 单链表 3.1.1 定义 注&#xff1a; 元素离散的分布在存储空间中&#xff0c;所以单链表是非随机存取的存储结构。 即不能直接找到表中某个特定的结点&#xff0c;需要从表头开始遍历&#xff0c;依次查找。 定义的代码 typedef struct LNode {ElemType data;//每个节点存放…
阅读更多...
第三章 处理机调度与死锁

第三章 处理机调度与死锁

目录 一、调度的概念、层次 2.1 调度的基本概念 2.2 调度的三个层次 2.2.1 高级调度 2.2.2 低级调度 2.2.3 中级调度 2.2.3.1 进程的挂起态 2.2.4 三层调度的联系、对比 二、进程调度的时机、切换与过程、方式 2.1 进程调度的时机 2.2 进程调度的方式 2.2.1 非抢占…
阅读更多...
计网复习题

计网复习题

一、单项选择题 OSI参考模型的物理层负责&#xff08;&#xff09;。 A&#xff0e;格式化报文 B&#xff0e;为数据选择通过网络的路由(网络层) C&#xff0e;定义连接到介质的特性 D&#xff0e;提供远程文件访问能力(应用层) 下列选项中&#xff0c;不属于网络体系结构中所…
阅读更多...
常用git操作总结

常用git操作总结

文章目录 一、git 分支命名规范&#xff08;1&#xff09;master 主分支&#xff08;2&#xff09;develop 开发分支&#xff08;3&#xff09;feature 分支&#xff08;一般简写为feat&#xff09;&#xff08;4&#xff09;hotfix 分支&#xff08;一般简写为fix&#xff09;…
阅读更多...
如何用canvas实现一个富文本编辑器

如何用canvas实现一个富文本编辑器

富文本编辑器相信大家都用过&#xff0c;相关的开源项目也很多&#xff0c;虽然具体的实现不一样&#xff0c;但是大部分都是使用DOM实现的&#xff0c;但其实还有一种实现方式&#xff0c;那就是使用HTML5的canvas&#xff0c;本文会带大家使用canvas简单实现一个类似Word的富…
阅读更多...
分布式系统学习第四天 fastcgi学习

分布式系统学习第四天 fastcgi学习

目录 1. Nginx作为web服务器处理请求 2. http协议复习 3. fastCGI 3.1 CGI 3.3 fastCGI和spawn-fcgi安装 3.4 nginx && fastcgi 3.5我的总结 其他知识点 1. Nginx作为web服务器处理请求 nginx不能处理动态请求 因此把请求发送给fastCGI对动态请求进行处理 静态…
阅读更多...
区块链基础之密码学及安全技术

区块链基础之密码学及安全技术

1.2 密码学及安全技术 1.2.1 密码学知识 1.2.1.1 Hash函数 Hash(哈希) 哈希函数是一类数学函数&#xff0c;可以在有限合理的时间内&#xff0c;将任意长度的消息压缩为 固定长度的输出值&#xff0c;并且是不可逆的。其输出值称为哈希值&#xff0c;也称为散列值。 哈希算法…
阅读更多...
越权漏洞学习-做你做不了的事情

越权漏洞学习-做你做不了的事情

&#xff08;一&#xff09;、什么是越权漏洞 1、了解越权漏洞&#xff1a; 越权漏洞是指一个用户或者一个攻击者通过利用系统中某一漏洞&#xff0c;可以获得超过其正常权限的权限。也就是说&#xff0c;越权漏洞会使攻击者能够执行未经授权的操作或访问受保护的资源 简单来…
阅读更多...
从开发人员的视角面对c盘容量紧缺的一些方案

从开发人员的视角面对c盘容量紧缺的一些方案

前言 随着时代的发展&#xff0c;固态价格不断地下降&#xff0c;电脑硬盘容量水平线在不断地上升&#xff0c;近几年新出的主流笔记本自带固态容量也基本上在256G以上。所以通常不会有容量不够而带来的烦恼。个人用户往往是因为视频、游戏等文件占用了大量容量&#xff0c;针…
阅读更多...
mmrotate调研

mmrotate调研

mmrotate调研 MMrotate是什么&#xff1f; ​ 在真实场景中&#xff0c;我们见到的图像不都是方方正正的&#xff0c;比如扫描的图书和遥感图像&#xff0c;需要检测的目标通常是有一定旋转角度的。这时候就需要用到旋转目标检测方法&#xff0c;对目标进行精确的定位&#x…
阅读更多...
第三方库介绍——mosquitto

第三方库介绍——mosquitto

文章目录 概述程序&#xff08;指令&#xff09;说明安装服务端与客户端服务端指令配置配置文件&#xff1a;mosquitto.conf认证配置&#xff1a;pwfile权限配置&#xff1a;aclfile启动服务器&#xff0c;选择配置文件&#xff1a;mosquitto.conf 测试发布指令&#xff1a;订阅…
阅读更多...
基于立创EDA的原理图设计进阶（实战开发一个小项目）

基于立创EDA的原理图设计进阶（实战开发一个小项目）

目录 学习目标 原理图设计进阶——空气质量检测仪 项目需求 1、功能性需求分析 2、非功能性需求 硬件框架图 元器件选型 MCU sensor LCD WIFI KEY PWOER 原理图设计 元件PCB封装设计-DIP&#xff0c;SOP 理论知识 直插式 贴片式 学习目标 1、熟悉电子产品设…
阅读更多...
网络编程详细讲解

网络编程详细讲解

网络编程 网络通信 网络 ip 地址 1.概念&#xff1a;用于唯一标识网络中的每台计算机/主机 2.查看ip地址&#xff1a;ipconfig 3.ip地址的表示形式&#xff1a;点分十进制XX.XX.XX.XX 4.每一个十进制数的范围&#xff1a;0~255 5.ip地址的组成网络地址主机地址&#xff0…
阅读更多...
团体程序设计天梯赛-练习集L2篇①

团体程序设计天梯赛-练习集L2篇①

&#x1f680;欢迎来到本文&#x1f680; &#x1f349;个人简介&#xff1a;Hello大家好呀&#xff0c;我是陈童学&#xff0c;一个与你一样正在慢慢前行的普通人。 &#x1f3c0;个人主页&#xff1a;陈童学哦CSDN &#x1f4a1;所属专栏&#xff1a;PTA &#x1f381;希望各…
阅读更多...
Python3学习之列表

Python3学习之列表

目录 1.访问列表中的值 2.更新列表 3.删除列表元素 4.Python列表脚本操作符 5.Python列表截取与拼接 6.嵌套列表 7.列表比较 8.Python列表函数&方法 序列是 Python 中最基本的数据结构。序列中的每个值都有对应的位置值&#xff0c;称之为索引&#xff0c;第一个索…
阅读更多...
Go语言doc

Go语言doc

1、Go语言doc go doc 命令可以打印附于 Go 语言程序实体上的文档&#xff0c;我们可以通过把程序实体的标识符作为该命令的参数来 达到查看其文档的目的。 所谓Go语言的程序实体&#xff0c;是指变量、常量、函数、结构体以及接口&#xff0c;而程序实体的标识符即是代表它们…
阅读更多...
JDBC 和数据库连接

JDBC 和数据库连接

JDBC 和数据库连接 基本介绍 JDBC为访问不同的数据库提供了统一的接口&#xff0c;为使用者屏蔽了细节问题。Java程序员使用JDBC&#xff0c;可以连接任何提供了JDBC驱动程序的数据库系统&#xff0c;从而完成对数据库的各种操作。JDBC的基本原理图&#xff3b;重要&#xff…
阅读更多...
CSDN 个性化推荐系统的设计和演进

CSDN 个性化推荐系统的设计和演进

个性化推荐项目 个性化推荐的设计和演进项目概览项目梳理依赖管理实现代码的重构和改进持续演化 个性化推荐的设计和演进 CSDN 的个性化推荐系统&#xff0c;是从既有的推荐项目中剥离出来的一个子项目&#xff0c;这个项目随后移交到了我们AI组。在近一年的时间内&#xff0c…
阅读更多...
机器学习实战｜第5周｜第3章：无监督学习与数据预处理｜3.3降维｜16:00~17:55

机器学习实战｜第5周｜第3章：无监督学习与数据预处理｜3.3降维｜16:00~17:55

目录 一、降维的动机 (1)数据压缩 (2)数据可视化 (3)降维的弊端 二、什么是维度的诅咒&#xff1f; 三、数据集被降维后能否逆转 四、降维的主要方法 (1)投影 (2)流形学习 五、PCA PCA可以用来给高度非线性数据集降维吗&#xff1f; 假设在一个1000维数据集上执行P…
阅读更多...
最优化理论中的惩罚函数法：概念、推导和应用

最优化理论中的惩罚函数法：概念、推导和应用

目录 1. 引言 2. 惩罚函数法的概念 2.1 惩罚函数法的基本思想 2.2 惩罚函数的定义 2.2.1 符号性质 2.2.2 惩罚性质 2.2.3 连续性质 2.3 惩罚函数法的推导 2.4 惩罚函数法的特点 2.4.1 灵活性 2.4.2 通用性 2.4.3 近似解 2.4.4 收敛性 3. 推导过程 3.1 问题建模 …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023