目录
一、降维的动机
(1)数据压缩
(2)数据可视化
(3)降维的弊端
二、什么是维度的诅咒?
三、数据集被降维后能否逆转
四、降维的主要方法
(1)投影
(2)流形学习
五、PCA
PCA可以用来给高度非线性数据集降维吗?
假设在一个1000维数据集上执行PCA,方差解释比设为95%。
产生的结果数据集维度是多少?
六、如何在数据集上评估算法的性能?
一、降维的动机
①数据压缩,数据压缩允许我们压缩数据,因而可以让算法使用更少的计算机内存或磁盘空间,提高算法学习速度;
②数据可视化,数据可视化会帮助机器学习工程师们更好地处理数据、设计算法。
(1)数据压缩
在工业上做特征搜集时经常产生这种高度冗余的数据集。
降维使得机器学习的算法运行更快。
(2)数据可视化
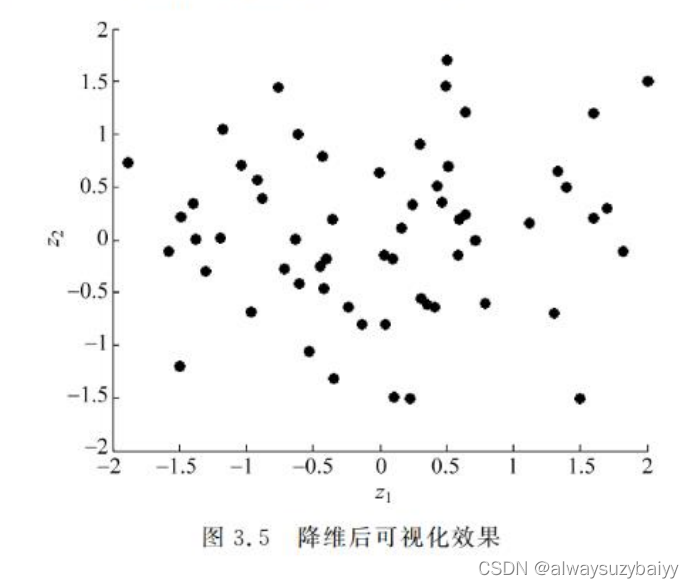
假设有关于许多不同国家的数据,每一个特征向量都有50个特征(如 GDP、人均GDP、平均寿命等)。如果要将这个50维的数据可视化是不可能的。使用降维的方法将其降至二维,便可以将其可视化了。

这样做的问题在于,降维的算法只负责减少维数,新产生的特征和
的意义就必须由我们自己去发现了。可视化后的效果如图 3.5 所示。
(3)降维的弊端
信息丢失:在降维的过程中,由于减少了维度,可能会丢失一些原始数据中的信息。因为降维后的数据可能不能完全捕捉原始数据的所有变化。
运算复杂度:降维的过程通常涉及到大量的矩阵和向量的计算,在高维数据中会更加复杂。这可能导致计算延迟和可能的计算资源瓶颈。
可解释性下降:由于降维后的低维数据难以从人类直观角度解释,因此可能会影响对数据的解释和理解。
小数据问题:在特征维度远大于样本数量的情况下,降维可能会使数据更加容易出现过度拟合现象,因为降维会减少数据样本的数量和维度。
计算策略的选择:降维技术包括主成分分析(PCA)、线性判别分析(LDA)和独立成分分析(ICA)等不同的计算策略。这些方法需要在执行时选择合适的策略和参数设置,以达到更好的效果。
综上所述,虽然降维可以帮助简化复杂的数据集并获得更高的效率或更好的可视化结果,但它也存在一些主要的弊端和挑战,需要慎重使用并尝试适当的技术改进来克服这些问题。
二、什么是维度的诅咒?
维度的诅咒(Curse of Dimensionality)是指随着特征维度的增加,数据分布在特征空间中变得稀疏,使得许多机器学习算法在高维空间中难以拟合数据并表现出低准确性的现象。
随着特征维度的增加,需要更多的数据以保持训练数据的广度和多样性。否则,由于数据的稀疏性和噪声数据的增加,高维空间中会出现更多的重叠和间隔,从而导致模型的准确性下降和泛化误差增加。此外,高维数据还需要消耗更多的计算资源来处理,并且容易出现过度拟合问题。
为了克服维度的诅咒,可以尝试以下方法:
特征选择:选择与预测变量高度相关的特征,以减少特征数量并提高算法的效率和准确性。
维度缩减:使用降维技术(例如主成分分析PCA、线性判别分析LDA等)将高维数据映射到低维空间,在保留数据重要特征的同时减少维度。
正则化:通过添加惩罚项以避免过度拟合的发生,并提高模型泛化能力。
从小样本开始:如可行,从较低维度的数据开始学习模型,逐渐扩展到更高维度的数据,可以加快模型训练速度和避免维度的诅咒。
总之,减少维度对于提高机器学习算法的准确性和效率至关重要,并且需要注意选择和使用合适的降维和特征选择技术。
三、数据集被降维后能否逆转
数据集被降维后,通常是不可能完全逆转回原始高维数据集的。这是因为降维的过程涉及到数据信息的损失,而恢复出这些损失的信息是不可能的。如果操作不当,甚至可能出现信息严重丢失而导致数据无法恢复的情况。
但是,可以通过某些技术实现部分逆转。
一种方法是重建(reconstruction)技术,这种技术使用低维特征空间的子空间与降维后的数据点之间的映射来重新构建高维数据点。例如,在PCA中,可以使用逆变换矩阵将低维特征向量映射回原始高维空间。该方法可以在一定程度上恢复高维数据的信息,但通常不能完美地恢复数据及其特征。
另一种方法是使用生成对抗网络(GANs)和自动编码器等生成模型来生成新的高维数据。这些技术使用低维特征向量来生成新的高维数据点。一般来说,虽然生成出的数据无法与原始高维数据完全匹配,但通常可以生成近似的高维数据以及保留的特征。
综上所述,尽管降维后的数据在某些情况下可能会部分逆转,但通常这种逆转是有限的,并且需要使用特定的技术来实现。因此,在进行降维操作时,需要谨慎选择,并在可能的情况下尽量保留数据的原始特征和信息。
四、降维的主要方法
投影和流形学习。
(1)投影
训练实例在所有维度并不是均匀分布的。许多特征几乎是不变的,也有许多特征是高度相关联的(如前面讨论的 MNIST 数据集)。因此,高维空间的所有训练实例实际上(或近似于)受一个低得多的低维子空间影响。这听起来很抽象,下面来看一个例子。在图3.6中,你可以看到一个由圆圈表示的 3D 数据集。
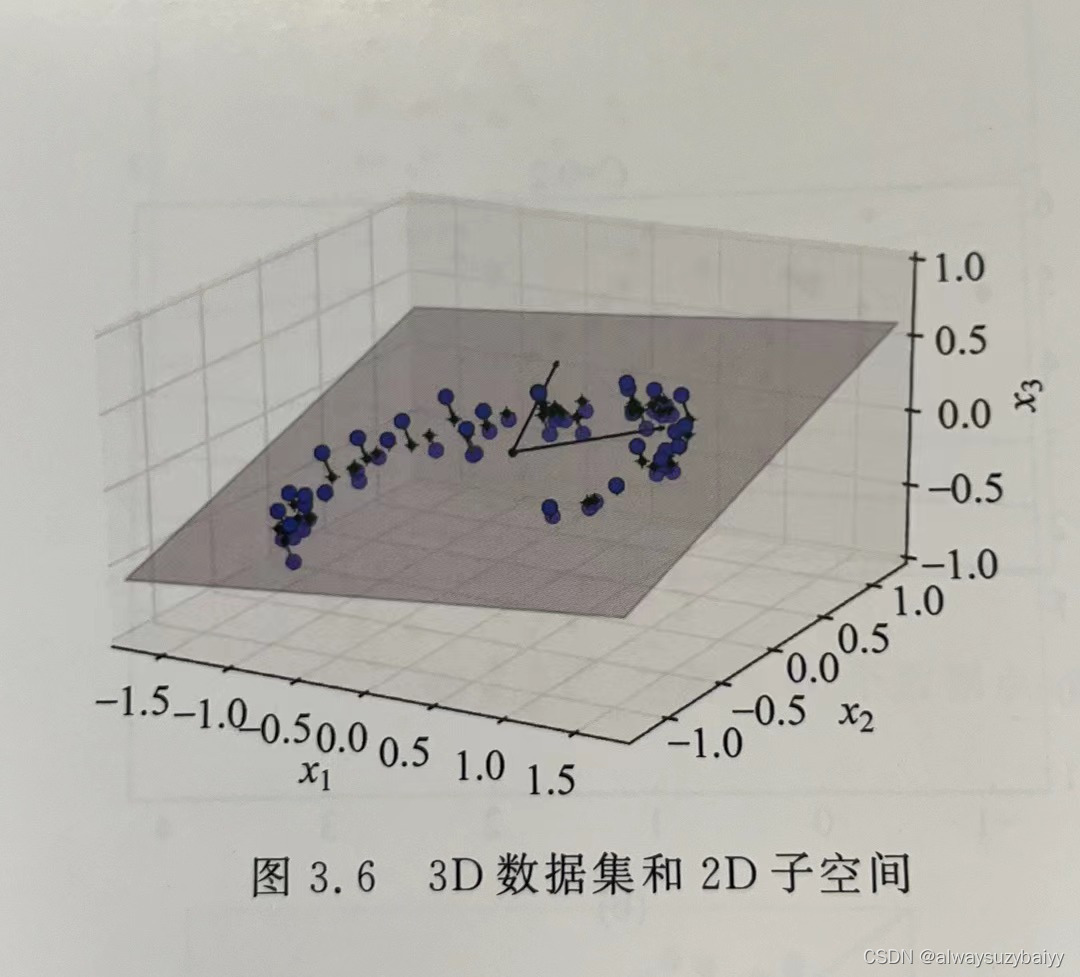
所有的训练实例都紧挨着一个平面:这就是高维(3D)空间的低维(2D)子空间。如果将每个训练实例垂直投影到这个子空间(如图 3.6 中实例到平面之间的短线所示),将得到如图3.7 所示的新2D 数据集,它已经将数据集维度从三维降到了二维。注意,图中的轴对应的是新特征 和
(平面上投影的坐标)。

不过投影并不总是降维的最佳方法。在许多情况下,子空间可能会弯曲或转动,比如图3.8所示的著名的瑞士卷数据集。

简单地进行平面投影(例如放弃)会直接将瑞士卷的不同层压扁在一起,如图 3.9(a)所示。但是你真正想要的是将整个瑞士卷展开铺平以后的 2D数据集,如图 3.9(b)所示。

(2)流形学习
瑞士卷就是一个二维流形的例子。简单地说,二维流形就是一个能够在更高维空间里面弯曲和扭转的二维形状。更概括地说,d 维流形就是n(其中,d<n)维空间的一部分,局部类似于一个d维超平面。在瑞士卷的例子中,d=2,n=3:它局部类似于一个二维平面,但是在第三个维度上卷起。
在训练模型之前降低训练集的维度,肯定可以加快训练速度,但这并不总是会导致更好或更简单的解决方案,它取决于数据集。
五、PCA
主成分分析:找出一个最主要的特征,然后进行分析,是分析、简化数据集的技术。
主要步骤:
去除平均值
计算协方差矩阵
计算协方差矩阵的特征值和特征向量
将特征值排序
保留前N个最大的特征值对应的特征向量
将数据转换到上面得到N个特征向量构建的新空间中(实现特征压缩)
PCA可以用来给高度非线性数据集降维吗?
PCA是一种线性降维技术,仅适用于可以用线性组合表示的数据。在某些非线性数据集上,应用PCA分析往往不能保持足够的信息和结构,导致降维效果较差,甚至是不准确的。
为了处理高度非线性数据集的降维问题,必须使用其他更为复杂的降维技术。例如,可以使用核PCA(KPCA)技术,它是PCA的一种扩展,可以克服线性PCA在非线性数据上的缺陷和限制。KPCA使用核技巧将数据映射到高维特征空间中,并在该空间中执行线性PCA,从而利用相同的线性代数操作在高维空间中实现非线性数据降维。这种方式可以处理更复杂的、非线性的数据分布,并且相对于其他非线性降维方法,仍可以保持一定的计算效率。
总之,尽管PCA在某些情况下可以用于非线性数据集的降维,但是对于大多数非线性数据集,PCA可能不是最合适的降维技术。应该选择其他基于非线性的降维技术,例如LLE、IsoMap、t-SNE和UMAP。
假设在一个1000维数据集上执行PCA,方差解释比设为95%。
产生的结果数据集维度是多少?
假设在一个1000维数据集上执行PCA并且方差解释比设为95%。要得到结果数据集的维度,需要进行以下几个步骤:
计算原始数据集的协方差矩阵。
对协方差矩阵进行特征值分解,得到特征向量和对应的特征值。
按照特征值从大到小的顺序对特征向量进行排序。
计算每个特征向量的方差解释比。
累计方差解释比,直到达到设定的百分比为止。
选择累计方差解释比达到95%时的特征向量,可以得到结果数据集。
结果数据集维度的计算方法为选择的特征向量数量。
因为选择的特征向量数量不确定,所以需要通过累计方差解释比的方式来确定。一般情况下,结果数据集的维度要比原始数据集低得多。在这个例子中,如果方差解释比设为95%,则选择足以解释95%累计方差的特征向量的数量。这个数量可以通过对数据集所有特征值进行排序并计算它们的方差解释比来确定。
六、如何在数据集上评估算法的性能?
算法的性能评估对于确定其质量和可行性至关重要。在数据集上评估算法的性能需要进行以下步骤:
(1)准备数据集:确定要用于评估算法的数据集,并将其随机地分成训练集和测试集。训练集用于拟合模型,测试集用于评估模型的性能。
(2)选择度量指标:选择适当的性能度量指标,根据应用场景,选择不同的度量指标。例如,分类问题中常见的性能指标有准确率、精度、召回率、F1-Score等;回归问题中常见的性能指标包括均方误差MSE、平均绝对误差MAE等。
(3)训练模型:使用训练数据集训练算法模型,可以使用不同的机器学习算法和技术进行训练。
(4)评估模型:使用测试数据集评估模型的性能。将模型应用于测试数据集中的样本,并使用选择的度量指标评估模型的预测效果。
(5)调整模型:根据评估的结果,如果模型表现不好,需要进一步调整模型。可以调整算法的超参数或应用更复杂/更可靠的机器学习算法来得到更好的性能。
(6)重复实验:为了获取更准确和更可靠的结果,需要多次重复实验,并使用不同的数据集进行评估和验证。
总之,评估机器学习算法的性能需要准备数据集、选择度量指标、训练模型、评估模型、调整模型和重复实验等步骤。这些步骤可以帮助确定算法的适用性和可行性,并促进其应用于不同的场景和问题。