1.逻辑回归(Logistics Regression)
逻辑回归用于解决二分类问题
1.1 Sigmoid函数
sigmoid函数在神经网络中如何起作用?详见本人笔记:机器学习和AI底层逻辑
复杂非线性分类->多个线段->每个线段是叠加而来的->sigmoid函数作为小线段的来源->不同的sigmoid可以叠加成任意形状的小线段,多个小线段拼接得到最终复杂分类的线段->这个过程用抽象的方法表达(神经网络)
sigmoid函数将数据 x \boldsymbol{x} x映射到 [ 0 , 1 ] [0,1] [0,1],概率范围刚好也是 [ 0 , 1 ] [0,1] [0,1],可以用概率大小与阈值比较来判断数据属于哪个类别

x
\boldsymbol{x}
x为数据、y为标签(表示哪个分类)、
θ
\boldsymbol{\theta}
θ为未知参数向量(先假设一个初始向量随后通过训练得到最优结果)、
θ
T
x
\boldsymbol{\theta}^{T}\boldsymbol{x}
θTx为分类边界、
若数据线性可分的则分类边界为直线
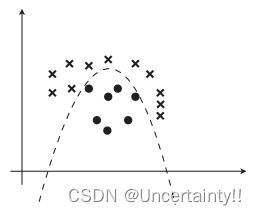
若数据线性不可分则分类边界为曲线
若
θ
T
x
<
0
\boldsymbol{\theta}^{T}\boldsymbol{x}\lt 0
θTx<0,则
f
θ
(
x
)
<
0.5
f_{\boldsymbol{\theta}}(\boldsymbol{x})\lt0.5
fθ(x)<0.5,
f
θ
(
x
)
=
P
(
y
=
0
∣
x
)
f_{\boldsymbol{\theta}}(\boldsymbol{x})=P(y=0|\boldsymbol{x})
fθ(x)=P(y=0∣x)(数据属于分类0的概率),概率在
[
0
,
0.5
]
[0,0.5]
[0,0.5]范围,则数据判别为属于分类0
若
θ
T
x
>
0
\boldsymbol{\theta}^{T}\boldsymbol{x}\gt 0
θTx>0,则
f
θ
(
x
)
>
0.5
f_{\boldsymbol{\theta}}(\boldsymbol{x})\gt0.5
fθ(x)>0.5,
f
θ
(
x
)
=
P
(
y
=
1
∣
x
)
f_{\boldsymbol{\theta}}(\boldsymbol{x})=P(y=1|\boldsymbol{x})
fθ(x)=P(y=1∣x)(数据属于分类1的概率),概率在
[
0.5
,
1
]
[0.5,1]
[0.5,1]范围,则数据判别为属于分类1

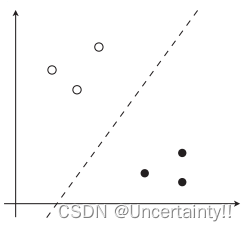
| 
|

通过训练调整参数达到最优结果
1.2 似然函数
对于二分类的情况,标签y的取值只有0、1,满足
P
(
y
=
0
∣
x
)
+
P
(
y
=
1
∣
x
)
=
1
P(y=0|\boldsymbol{x})+P(y=1|\boldsymbol{x})=1
P(y=0∣x)+P(y=1∣x)=1
数据与标签的理想关系
标签
y
=
0
y=0
y=0 时,我们希望数据为标签0的概率
f
θ
(
x
)
=
P
(
y
=
0
∣
x
)
f_{\boldsymbol{\theta}}(\boldsymbol{x})=P(y=0|\boldsymbol{x})
fθ(x)=P(y=0∣x)最大
标签
y
=
1
y=1
y=1 时,我们希望数据为标签1的概率
f
θ
(
x
)
=
P
(
y
=
1
∣
x
)
f_{\boldsymbol{\theta}}(\boldsymbol{x})=P(y=1|\boldsymbol{x})
fθ(x)=P(y=1∣x)最大
所有训练数据中的每个数据取到正确标签的概率乘积起来就是所有数据取到正确标签的概率(联合概率),即逻辑回归的目标函数/代价函数:似然函数
最大化似然估计求似然函数的极大值,进而得到参数估计值,求代价函数的最小值就是对似然函数的极大化
下面我们求似然函数的最大值

首先对似然函数取对数,由于对数函数也是单增函数,我要求最大化似然函数,所有取对数后不影响似然函数的增减性

对上述结果进行微分

∂
u
∂
θ
j
=
∑
i
=
1
n
(
y
(
i
)
−
f
θ
(
x
(
i
)
)
)
x
j
(
i
)
\frac{\partial u}{\partial \theta_j}=\sum_{i=1}^{n}\big(y^{(i)}-f_{\theta}(\boldsymbol{x}^{(i)})\big)x_j^{(i)}
∂θj∂u=i=1∑n(y(i)−fθ(x(i)))xj(i)
采用梯度下降法迭代参数,最终获得最优参数
参数的更新表达式

若想要与普通回归的参数更新表达式统一,则将括号内提出负号,将负号写到学习率前