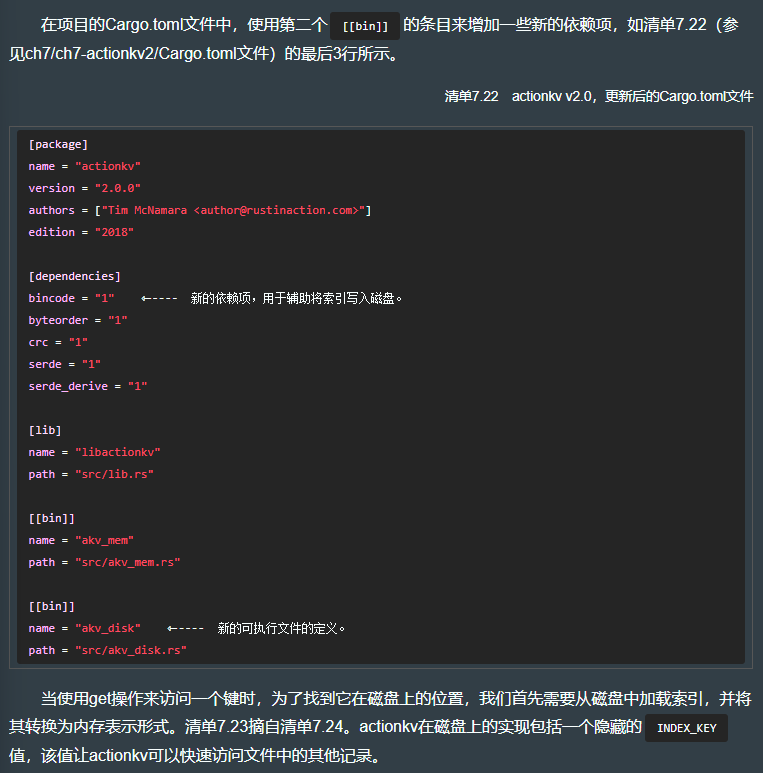
主要见斯坦福大学Wilson Nguyen、Dan Boneh和微软研究中心Srinath Setty 2023年论文《Revisiting the Nova Proof System on a Cycle of Curves》。

前序博客见：

• 基于cycle of curves的Nova证明系统（1）

5. IVC Proof进一步压缩

本文提出了两种压缩IVC proof的方案：

• 1）compression without SNARKs
• 2）compression with SNARKs

https://github.com/Microsoft/Nova代码中的CompressSNARK采用了这两种压缩方式。

5.1）compression without SNARKs

已知某convincing proof：
${\pi }_i=(($𝕦${}_i^{(2)},$𝕨${}_i^{(2)}),({\mathbb{U}}_i^{(1)},{\mathbb{W}}_i^{(1)}),({\mathbb{U}}_i^{(2)},{\mathbb{W}}_i^{(2)}))$

Prover $\mathcal{P}$端执行如下步骤，获得压缩proof ${\pi }_i^{\prime }$：

• 1）为${\text{R1CS}}^{(2)}$ fold pairs：将${\text{R1CS}}^{(2)}$的committed pairs $($𝕦${}_i^{(2)},$𝕨${}_i^{(2)}),({\mathbb{U}}_i^{(2)},{\mathbb{W}}_i^{(2)})$ 进行fold：
  ${\text{Fold}}_{\mathcal{P}}(\text{pk},($𝕦${}_i^{(2)},$𝕨${}_i^{(2)}),({\mathbb{U}}_i^{(2)},{\mathbb{W}}_i^{(2)}))\to ({\bar{T}}_i^{(2)},(\cdot ,{\mathbb{W}}_{i+1}^{(2)}))$
• 2）输出压缩proof：
  ${\pi }_i^{\prime }=($𝕦${}_i^{(2)},{\mathbb{U}}_i^{(2)},({\bar{T}}_i^{(2)},{\mathbb{W}}_{i+1}^{(2)}),({\mathbb{U}}_i^{(1)},{\mathbb{W}}_i^{(1)}))$

Verifier $\mathcal{V}$端执行如下步骤，来验证 压缩proof ${\pi }_i^{\prime }$：

• 1）执行初始folding流程：${\mathbb{U}}_{i+1}^{(2)}:={\text{Fold}}_{\mathcal{V}}(\text{vk},$𝕦${}_i^{(2)},{\mathbb{U}}_i^{(2)},{\bar{T}}_i^{(2)})$
• 2）若满足以下6个条件，则验证通过：
  • 2.1）索引值$i$必须大于0；
  • 2.2）𝕦${}_i^{(2)}.x_0=H_1(\text{vk},i^{(1)},z_0^{(1)},z_i^{(1)},{\mathbb{U}}_i^{(2)})$
  • 2.3）𝕦${}_i^{(2)}.x_1=H_2(\text{vk},i^{(2)},z_0^{(2)},z_i^{(2)},{\mathbb{U}}_i^{(1)})$
  • 2.4）$({\mathbb{U}}_i^{(1)},{\mathbb{W}}_i^{(1)})$ pair 满足${\text{R1CS}}^{(1)}$
  • 2.5）$({\mathbb{U}}_i^{(2)},{\mathbb{W}}_i^{(2)})$ pair 满足${\text{R1CS}}^{(2)}$
  • 2.6）“$($𝕦${}_i^{(2)},$𝕨${}_i^{(2)})$ pair 严格 满足${\text{R1CS}}^{(2)}$ ” 改为 ”𝕦${}_i^{(2)}.\bar{E}={\bar{0}}^{(2)}$ 且 𝕦${}_i^{(2)}.s={\bar{1}}^{(2)}$“

压缩proof的递归运算：

• 压缩proof ${\pi }_i^{\prime }$ 和 新的evaluation值：$z_{i+1}^{(1)}:=F_1(z_i^{(1)},{\text{aux}}_i^{(1)})$ 以及 $z_{i+1}^{(2)}:=F_2(z_i^{(2)},{\text{aux}}_i^{(2)})$，足以供Nova prover执行another step for Iteration $i+1$。【注意，压缩proof ${\pi }_i^{\prime }$是readily incremental的。】
• 为便于理解，本论文中基于未压缩proof ${\pi }_i$构建了IVC方案，也可基于压缩proof ${\pi }_i^{\prime }$来构建IVC方案。Nova论文，在”compression without SNARKs“之后，使用了某SNARK来将proof ${\pi }_i^{\prime }$进一步压缩为${\pi }_i^{{}^{\prime \prime }}$。

5.2）compression with SNARKs

针对relation ${\mathcal{R}}_{sat}$的通用SNARK可用于进一步压缩IVC proof。Nova论文中采用Spartan SNARK来压缩IVC proof。

已知”compression without SNARKs“的压缩proof：
${\pi }_i^{\prime }=($𝕦${}_i^{(2)},{\mathbb{U}}_i^{(2)},({\bar{T}}_i^{(2)},{\mathbb{W}}_{i+1}^{(2)}),({\mathbb{U}}_i^{(1)},{\mathbb{W}}_i^{(1)}))$

Prover $\mathcal{P}$端执行如下步骤，获得压缩proof ${\pi }_i^{{}^{\prime \prime }}$：

Verifier $\mathcal{V}$端执行如下步骤，来验证 压缩proof ${\pi }_i^{\prime }$：

• 1）执行初始folding流程：${\mathbb{U}}_{i+1}^{(2)}:={\text{Fold}}_{\mathcal{V}}(\text{vk},$𝕦${}_i^{(2)},{\mathbb{U}}_i^{(2)},{\bar{T}}_i^{(2)})$
• 2）若满足以下6个条件，则验证通过：
  • 2.1）索引值$i$必须大于0；
  • 2.2）𝕦${}_i^{(2)}.x_0=H_1(\text{vk},i^{(1)},z_0^{(1)},z_i^{(1)},{\mathbb{U}}_i^{(2)})$
  • 2.3）𝕦${}_i^{(2)}.x_1=H_2(\text{vk},i^{(2)},z_0^{(2)},z_i^{(2)},{\mathbb{U}}_i^{(1)})$
  • 2.4）$({\mathbb{U}}_i^{(1)},{\mathbb{W}}_i^{(1)})$ pair 满足${\text{R1CS}}^{(1)}$
  • 2.5）$({\mathbb{U}}_i^{(2)},{\mathbb{W}}_i^{(2)})$ pair 满足${\text{R1CS}}^{(2)}$
  • 2.4）${\pi }_{sat}$为 relation ${\mathcal{R}}_{sat}$ with instance $({\mathbb{U}}_{i+1}^{(2)},{\mathbb{U}}_i^{(2)})$ 的convincing SNARK proof。
  • 2.5）2.6）“$($𝕦${}_i^{(2)},$𝕨${}_i^{(2)})$ pair 严格 满足${\text{R1CS}}^{(2)}$ ” 改为 ”𝕦${}_i^{(2)}.\bar{E}={\bar{0}}^{(2)}$ 且 𝕦${}_i^{(2)}.s={\bar{1}}^{(2)}$“

6. Nova IVC proof的延展性 及 应对措施

Nova的IVC proof具有延展性问题。

假设某adversary知道某valid Nova IVC proof ${\pi }_i$ 以及相应的参数：

• IVC公共参数$pp$
• 函数描述：$F_1:{\mathbb{F}}_1^{a_1}\times {\mathbb{F}}_1^{b_1}\to {\mathbb{F}}_1^{a_1}$ 和 $F_2:{\mathbb{F}}_2^{a_2}\times {\mathbb{F}}_2^{b_2}\to {\mathbb{F}}_2^{a_2}$。
• 索引号 $i\in \mathbb{N}$。
• 起始值$z_0^{(1)}\in {\mathbb{F}}_1^{a_1}$和$z_0^{(2)}\in {\mathbb{F}}_2^{a_2}$
• claimed evaluations值$z_i^{(1)}\in {\mathbb{F}}_1^{a_1}$和$z_i^{(2)}\in {\mathbb{F}}_2^{a_2}$

针对相同的iteration $i$，该adversary可对不同于$z_i^{(2)}$的$z_{prime}^{(2)}$构建proof ${\pi }_{prime}$，而IVC Verifier的参数为：
$(pp,(F_1,F_2),i,(z_0^{(1)},z_0^{(2)}),(z_i^{(1)},z_{prime}^{(2)}),{\pi }_{prime})$
为让IVC Verifier验证通过。

需强调：

• 为计算$z_i^{(2)}$，adversary无需知道所有的辅助值$({\text{aux}}_0^{(2)},{\text{aux}}_1^{(2)},\cdots ,{\text{aux}}_{i-1}^{(2)})$。在不知道前$i-1$个辅助的情况下，修改替换最后一个辅助值${\text{aux}}_{prime}^{(2)}\ne {\text{aux}}_{i-1}^{(2)}$，可为iteration $i$的替换值$z_{prime}^{(2)}$构建proof ${\pi }_{prime}$。

延展性会带来现实世界漏洞。假设：

• Alice使用其秘密辅助值来计算$z_i^{(2)}$，且$z_i^{(2)}$中编码了其payment地址。
• Alice将$z_i^{(2)}$和相应的proof发送给某payment合约。
• 攻击者可拦截Alice的消息，将$z_i^{(2)}$替换为 编码了攻击者payment地址的$z_{prime}^{(2)}$，以及有效的proof ${\pi }_{prime}$ 发送个payment合约。payment合约会将资金发送给攻击者，而不是给Alice。
  事实上，若Tornado Cash中使用statement可延展的证明系统，则可能盗取资金。

若函数$F$为确定性函数——即输入中不包含辅助参数，则不存在延展性问题。因为此时，函数$F$的第$i$次迭代的结果$z_i$ 由初始值$z_0$完全确定。

而对具有辅助输入的Nova IVC，为解决其延展性问题，可采用如下3种策略：

• 1）压缩（Compression）：基于cycle of curves的Nova证明系统（1）的”4.3 修订版Nova Prover算法“中，Prover在输出final folded instance的同时会输出a satisfying witness。可替换为，Prover在输出final folded instance的同时输出 a zkSNARK proof that it has a valid witness for this folded instance。若该zkSNARK方案是simulation extractable，则该final proof是非延展性的。事实上，Nova的当前实现就是采用这种方案，在解决延展性问题的同时，对final proof进行了压缩。但是，这与IVC概念不兼容：压缩之后，另一方无法通过folding进一步继续迭代了。这样的结果就是，整个IVC chain的计算仅能由单一方完成。
• 2）上下文（context）：将verification key $\text{vk}$扩展为包含一个额外的context元素$\text{ctx}$。这样可确保非延展性，但是与IVC不兼容。额外的context元素包含了该计算的最后一步，且阻止了其它方使用folding进一步延长IVC chain。
• 3）递增上下文（Incremental context）：为确保非延展性的同时，支持IVC的incremental aspect，每次一方与另一方交互时更新verification key $\text{vk}$，从而各方都可延长IVC chain。

6.1 延展性攻击

本节展示对IVC chain最后一步的延展性攻击。

已知：
${\pi }_i=(($𝕦${}_i^{(2)},$𝕨${}_i^{(2)}),({\mathbb{U}}_i^{(1)},{\mathbb{W}}_i^{(1)}),({\mathbb{U}}_i^{(2)},{\mathbb{W}}_i^{(2)}))$

延展性攻击操作如下：

• 1）根据论文《Revisiting the Nova Proof System on a Cycle of Curves》第6章”Proof of Security“可知，可解析𝕨${}_i^{(2)}$ 来获取relational witness：
  ${\hat{w}}_i^{(2)}=(\text{vk},(i-1{)}^{(2)},z_0^{(2)},z_{i-1}^{(2)},{\text{aux}}_{i-1}^{(2)},{\mathbb{U}}_{i-1}^{(1)},$𝕦${}_{i-1}^{(1)},{\bar{T}}_{i-1}^{(1)})$
  其中$z_i^{(2)}=F_2(z_0^{(2)},{\text{aux}}_0^{(2)})$，${\mathbb{U}}_i^{(1)}={\text{Fold}}_{\mathcal{V}}(\text{vk},{\mathbb{U}}_{i-1}^{(1)},$𝕦${}_i^{(1)},{\bar{T}}_{i-1}^{(1)})$
  从而可根据𝕨${}_i^{(2)}$ 来解析获取${\hat{w}}_i^{(2)}$。

• 2）找到一个不同的辅助值：使用$z_{i-1}^{(2)}$，（假设对于$F_2$很容易）找到某${\text{aux}}_{prime}^{(2)}$，使得：
  $z_{prime}^{(2)}:=F_2(z_{i-1}^{(2)},{\text{aux}}_{prime}^{(2)})\ne F_2(z_{i-1}^{(2)},{\text{aux}}_{i-1}^{(2)})=z_i^{(2)}$

• 3）为${\text{R1CS}}^{(2)}$计算

Nova系列博客

• Nova: Recursive Zero-Knowledge Arguments from Folding Schemes学习笔记
• Nova 和 SuperNova：无需通用电路的通用机器执行证明系统
• Sangria：类似Nova folding scheme的relaxed PLONK for PLONK
• 基于Nova/SuperNova的zkVM
• SuperNova：为多指令虚拟机执行提供递归证明
• Lurk——Recursive zk-SNARKs编程语言
• Research Day 2023：Succinct ZKP最新进展
• 2023年 ZK Hack以及ZK Summit 亮点记
• 基于cycle of curves的Nova证明系统（1）