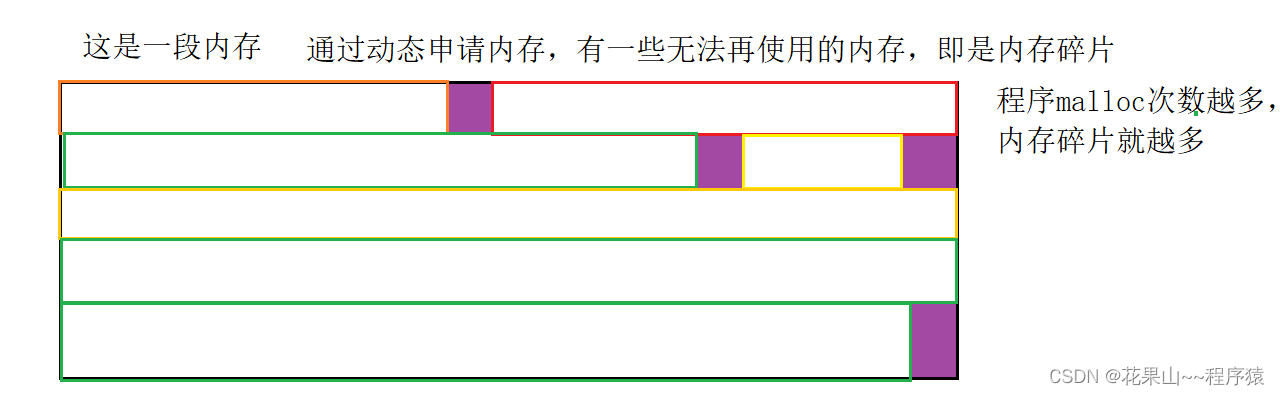
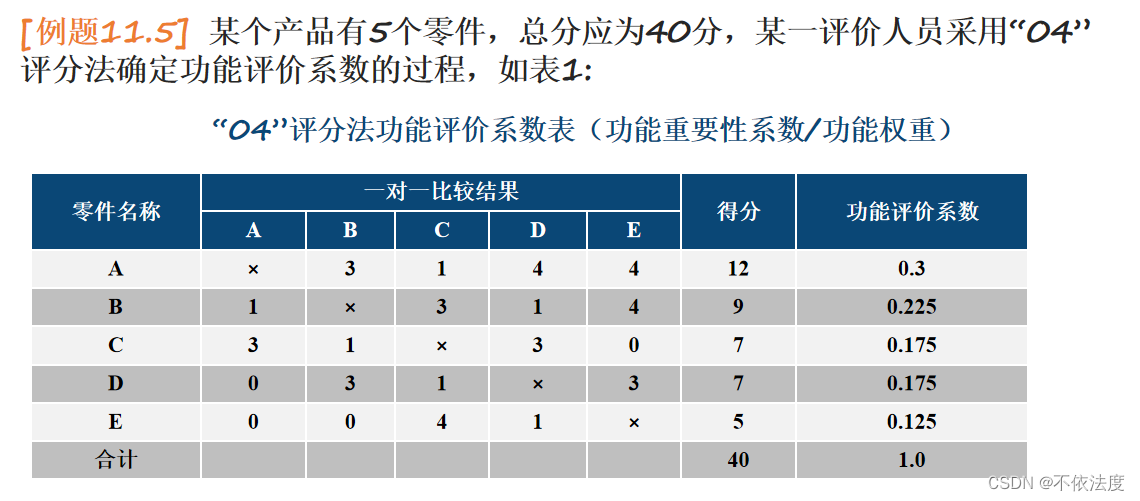
CNN的实现
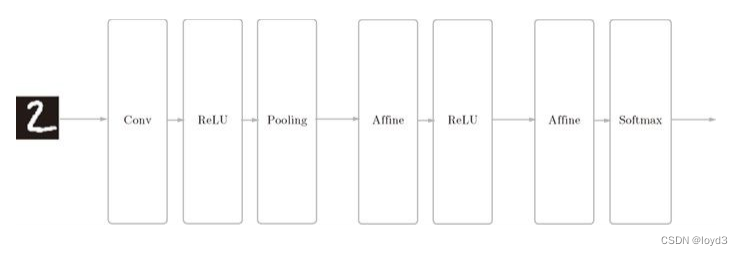
网络的构成是“Convolution - ReLU - Pooling -Affine - ReLU - Affine - Softmax”,我们将它实现为名为 SimpleConvNet的类。
首先来看一下 SimpleConvNet的初始化(init),取下面这些参数。
input_dim——输入数据的维度:(通道,高,长)
conv_param——卷积层的超参数(字典)。字典的关键字如下:
filter_num——滤波器的数量
filter_size——滤波器的大小
stride——步幅
pad——填充
hidden_size——隐藏层(全连接)的神经元数量
output_size——输出层(全连接)的神经元数量
weitght_int_std——初始化时权重的标准差
这里,卷积层的超参数通过名为 conv_param的字典传入。
SimpleConvNet的实现如下:
class SimpleConvNet:
def __init__(self, input_dim=(1,28,28), conv_param={'filter_num':30, 'filter_size':5,'pad':0, 'stride':1}, hidden_size=100,output_size=10, weight_init_std=0.01):
filter_num = conv_param['filter_num']
filter_size = conv_param['filter_size']
filter_pad = conv_param['filter_pad']
filter_stride = conv_param['filter_stride']
input_size = input_dim[1]
conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride +1
pool_output_size = int(filter_num * (conv_output_size /2) * (conv_output_size/2))
# 这里将由初始化参数传入的卷积层的超参数从字典中取了出来(以方便后面使用),然后,计算卷积层的输出大小。
# 接下来是权重参数的初始化部分
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(filter_num, input_dim[0],filter_size, filter_size)
self.params['b1'] = np.zeros(filter_num)
self.params['W2'] = weight_init_std * np.random.randn(pool_output_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
# 最后生成必要的层
self.layers = OrderDict()
self.layers['Conv1'] = Convolution(self.params['W1'],self.params['b1'],conv_param['stride'],conv_param['pad'])
self.layers['Relu1']= Relu()
self.layers['Pool1']= Pooling(poo_h=2,pool_w=2,stride=2)
self.layers['Affine1'] = Affine(self.params['W2'],self.params['b2'])
self.layers['Relu2'] = Relu()
self,layers['Affine2']= Affine(self.params['W3'],self.params['b3'])
self.last_layer = SoftmaxWithLoss()
# 从最前面开始按顺序向有序字典(OrderedDict)的layers中添加层。只有最后的SoftmaxWithLoss层被添加到别的变量LastLayer中。
以上就是simpleConvNet的初始化中进行的处理。像这样初始化后,进行推理的predict方法和求损失函数值的 Loss方法就可以像下面这样实现
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
y = self.predict(x)
return self.lastLayer.forward(y,t)
这里,参数x是输入数据,t是监督标签。用于推理的predict方法从头开始依次调用已添加的层,并将结果传递给下一层。
在求损失函数的loss方法中,除了使用predict方法进行的forward处理之外,还会继续进行forward处理,直到到达最后的SoftmaxwithLoss层。
下面是基于误差反向传播法求梯度的代码实现
def gradient(self,x,t):
#forward
self.loss(x,t)
#backward
dout = 1
dout = self.lastLayer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 设定
grads={}
grads['W1'] = self,layers['Conv1'].dw
grads['b1'] = self.layers['Conv1'].db
grads['W2'] = self.layers['Affine1'].dw
grads['b2'] = self,layers['Affine1'].db
grads['W3'] = self,layers['Affine2'].dw
grads['b3'] = self.layers['Affine2'].db
return grads
参数的梯度通过误差反向传播法(反向传播)求出
使用这个 SimpleConvNet学习 MNIST 数据集。训练数据的识别率为 99.82%,测试数据的识别率为 98.96%,测试数据的识别率大约为 99%,就小型网络来说,这是一个非常高的识别率。