目录
概念(在做习题中常用的概念)
两种特殊的二叉树
二叉树的性质
二叉树的遍历(重点)
如上图:
二叉树的构建(代码表示一颗二叉树和一些操作二叉树的方法)
二叉树的oj习题讲解(重点)
1. 检查两棵树是否相同 力扣
2. 另一颗树的子树 力扣
3. 反转二叉树 力扣
4. 判断一颗二叉树是否为平衡二叉树( 分别在O(N*2)和O(N)的时间复杂度代码来写 ) 力扣
5. 对称二叉树 力扣
6. 二叉树的构建及遍历(根据先序遍历创建一颗二叉树) 二叉树遍历_牛客题霸_牛客网
7. 二叉树的层序遍历 力扣
8. 二叉树中两个指定节点的最近公共祖先 力扣
9. 根据前序遍历和中序遍历构造一颗二叉树 力扣
10. 根据后序遍历和中序遍历构建一颗二叉树 力扣
11. 二叉树创建字符串 力扣
12. 二叉树的前序 非递归遍历 力扣
13. 二叉树的中序 非递归遍历 力扣
14. 二叉树的后序 非递归遍历 力扣
oj题代码详解:
前言
二叉树的一些oj题是在面试中常考的,同时概念也是很重要的,在做二叉树习题中掌握概念以及一些推导公式才能提高做题效率。
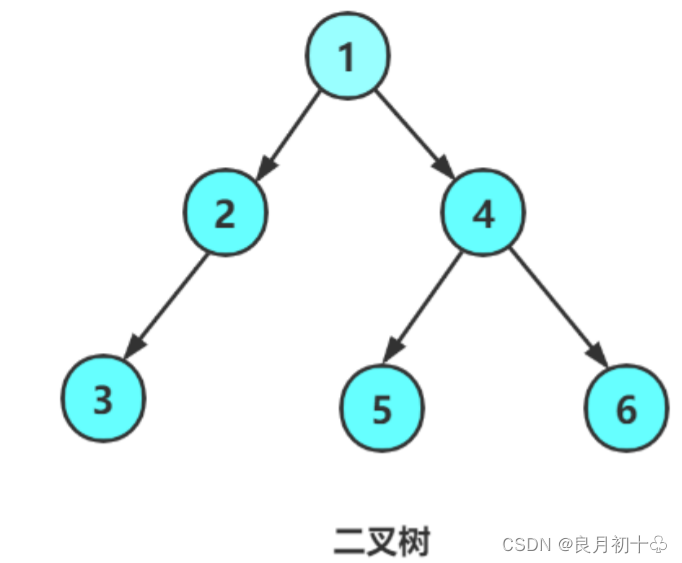
概念(在做习题中常用的概念)
| 节点的度 | 一个节点含有子树的个数 |
| 树的度 | 在一棵树中所有节点度的最大值 |
| 叶子节点(终端节点) | 度为0的节点称为叶子节点 |
| 父亲节点(双亲节点) | 一个含有子节点的节点,这个节点称为其子节点的父亲节点 |
| 根节点 | 一棵树中没有双亲节点的节点 |
| 节点的层 | 从根节点开始,根节点就是第一层,根的子节点是第二层,一次类推 |
| 树的高度(深度) | 树种节点的最大层次 |
二叉树如何用代码表示(定义一个静态内部类)
static class TreeNode{
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(char val) {
this.val = val;
}
}由于二叉树每个节点都有值域(value)、左子树(left)、右子树(right),所以将二叉树的节点定义成一个静态内部类,加上构造方法,就构成一颗二叉树中的完整的一个节点。
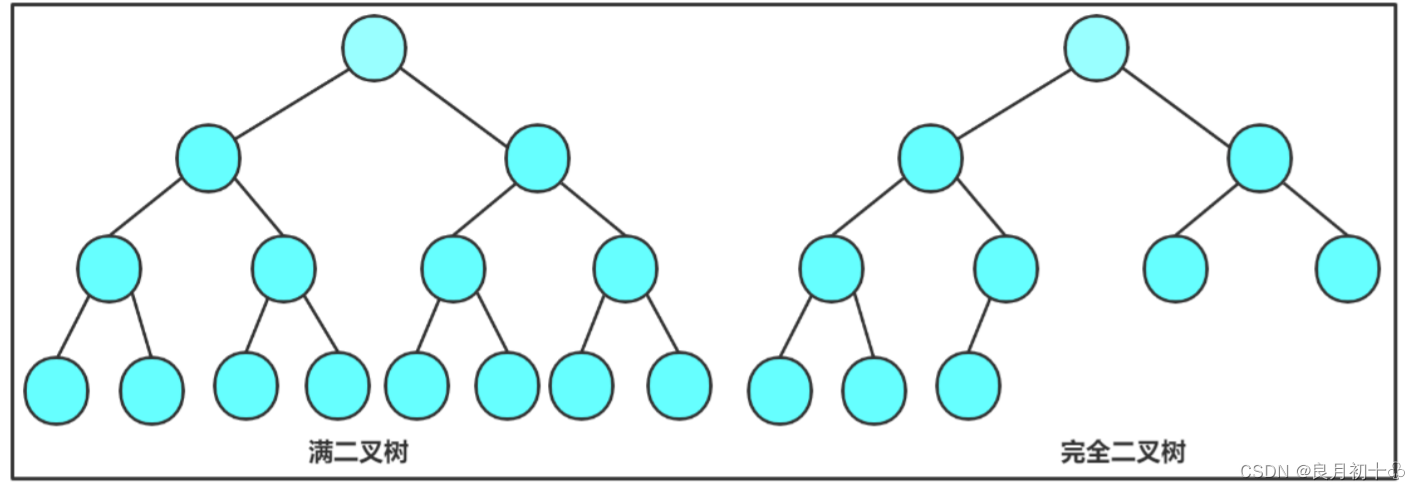
两种特殊的二叉树
1. 满二叉树
每层节点数都达到最大值,这颗二叉树就是满二叉树,或者一颗二叉树的层数为k,且节点总数是2^k - 1,此时这棵树就是满二叉树。
2. 完全二叉树
完全二叉树是由满二叉树引出的,从根节点开始编号,顺序从上往下,每一行是从左往右,没有编号为空的节点,此时这棵树就是完全二叉树。

二叉树的性质
| 1. 根节点的层数为1,则一颗非空二叉树的第i层节点个数最多为:2 ^ (i -1) |
| 2. 根节点的二叉树的深度为1,则深度为k的二叉树的最大节点数为:2^k - 1 |
| 3. 叶子节点个数为n0,度为2的节点个数为n2,则 n0 = n2 + 1 |
| 4. n个节点的完全二叉树的深度为 log2 (n + 1) |
| 5. n个节点的完全二叉树,如果按层序遍历编号,对于i号节点有: (1)双亲节点编号:(i-1)/ 2 (2)左孩子节点编号:2*i + 1 (3)右孩子节点编号:2 * i + 2 |
二叉树的遍历(重点)
| 1. 前序遍历(先根遍历) | 根 ---> 左 ---> 右 |
| 2. 中序遍历 | 左 ---> 根 ---> 右 |
| 3. 后序遍历 | 左 ---> 右 ---> 根 |
| 4. 层序遍历 | 按照顺序:从上往下,每一行从左往右依次编号 |
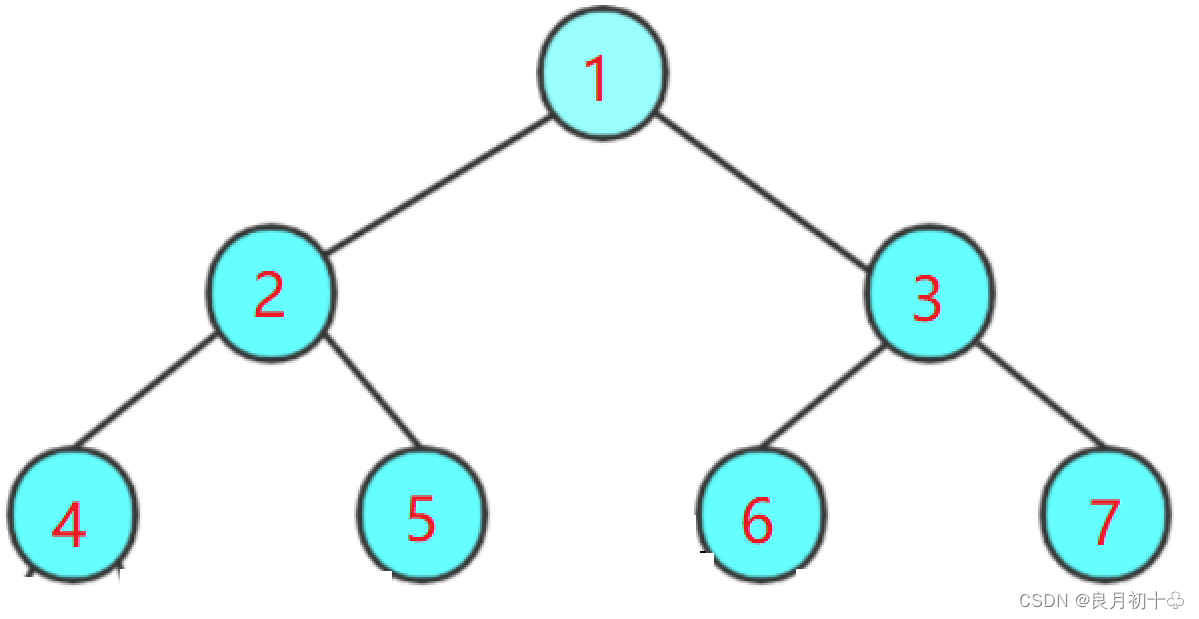
如上图:
1. 先序遍历: 1 2 4 5 3 6 7
2. 中序遍历: 4 2 5 1 6 3 7
3. 后序遍历: 4 5 2 6 7 3 1
4. 层序遍历: 1 2 3 4 5 6 7
二叉树的构建(代码表示一颗二叉树和一些操作二叉树的方法)
public class TextBinaryTree {
static class TreeNode{
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(char val) {
this.val = val;
}
}
public TreeNode root;//定义二叉树的根节点
//非正规创建一颗二叉树
public TreeNode createTree() {
TreeNode A = new TreeNode('A');
TreeNode B = new TreeNode('B');
TreeNode C = new TreeNode('C');
TreeNode D = new TreeNode('D');
TreeNode E = new TreeNode('E');
TreeNode F = new TreeNode('F');
TreeNode G = new TreeNode('G');
TreeNode H = new TreeNode('H');
A.left = B;
A.right = C;
B.left = D;
B.right = E;
E.right = H;
C.left = F;
C.right = G;
this.root = A;
return root;
}
//前序遍历
public void preOrder(TreeNode root) {
if (root == null) return;
System.out.print(root.val + " ");
preOrder(root.left);
preOrder(root.right);
}
//中序遍历
public void inOrder(TreeNode root) {
if (root == null) return;
inOrder(root.left);
System.out.print(root.val + " ");
inOrder(root.right);
}
//后序遍历
public void postOrder(TreeNode root) {
if (root == null) return;
postOrder(root.left);
postOrder(root.right);
System.out.print(root.val + " ");
}
//前序遍历有返回值
//此时这个list需要放在外边,否则每次递归都会产生一个新的list
List<Integer> list = new ArrayList<>();
public List<Integer> preorderTraversal(TreeNode root) {
if (root == null) return list;
list.add(root.val);
preorderTraversal(root.left);
preorderTraversal(root.right);
return list;
}
//二叉树的中序遍历有返回值
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
if (root == null) return list;
List<Integer> leftTree = inorderTraversal(root.left);
list.addAll(leftTree);
list.add(root.val);
List<Integer> rightTree = inorderTraversal(root.right);
list.addAll(rightTree);
return list;
}
//二叉树的后序遍历有返回值
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
if (root == null) return list;
List<Integer> leftTree = postorderTraversal(root.left);
list.addAll(leftTree);
List<Integer> rightTree = postorderTraversal(root.right);
list.addAll(rightTree);
list.add(root.val);
return list;
}
//获取二叉树中的节点个数
//子问题:左树的节点 + 右树的节点 + 1
//时间复杂度:O(N) 空间复杂度:O(logN),如果是单分支的树,空间复杂度就是
//O(N)
public int size(TreeNode root) {
if (root == null) return 0;
return size(root.left) + size(root.right) + 1;
}
//遍历思路
public int count = 0;
public int size1(TreeNode root) {
if (root == null) return 0;
//只要根不为空就++,然后遍历左树和右树
count++;
size1(root.left);
size1(root.right);
return count;
}
//获取叶子节点的个数 子问题思路
public int getLeafNodeCount(TreeNode root) {
if (root == null) return 0;//注意:当root为空的时候是没有叶子节点的
if (root.left == null && root.right == null)
return 1;
return getLeafNodeCount(root.left) +
getLeafNodeCount(root.right);
}
//遍历思路
public int leafCount;
public void leafNodeCount(TreeNode root) {
if (root == null) return;
if (root.left == null && root.right == null)
leafCount++;
leafNodeCount(root.left);
leafNodeCount(root.right);
}
//获取第k层的节点个数
//第k层的节点个数就相当于第k-1层的孩子的节点个数
public int getLevelNodeCount(TreeNode root, int k) {
if (root == null) return 0;
if (k == 1) return 1;
int left = getLevelNodeCount(root.left, k-1);
int right = getLevelNodeCount(root.right, k-1);
return left + right;
}
//获取二叉树的高度
//时间复杂度:O(n)(会遍历到每一个节点)
public int getHeight(TreeNode root) {
if (root == null) return 0;
int leftHeight = getHeight(root.left);
int rightHeight = getHeight(root.right);
return Math.max(leftHeight,rightHeight) + 1;
}
//二叉树的层序遍历
public void levelOrder1(TreeNode root) {
if (root == null) return;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode cur = queue.poll();
System.out.print(cur.val + " ");
if (cur.left != null) {
queue.offer(cur.left);
}
if (cur.right != null) {
queue.offer(cur.right);
}
}
}
//二叉树层序遍历有返回值
public List<List<Integer>> levelOrder2(TreeNode root) {
List<List<Integer>> list = new ArrayList<>();
if (root == null) return list;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
int size = queue.size();
List<Integer> ret = new ArrayList<>();
while (size != 0) {
TreeNode cur = queue.poll();
ret.add(cur.val);
size--;
if (cur.left != null) {
queue.offer(cur.left);
}
if (cur.right != null) {
queue.offer(cur.right);
}
}
list.add(ret);
}
return list;
}
}二叉树的oj习题讲解
1. 检查两棵树是否相同 力扣 | 思路:遍历两棵树的每一个节点,若一个空,一个不为空,不相同,两个节点都不为空,判断值是否相等,值不相等,也不是相同的树。 |
2. 另一颗树的子树 力扣 | 思路:先判断是不是相同的树,如果是相同的树也算是子树,如果不相同,判断是不是root的左子树,是不是root(根节点)的右子树。 |
3. 反转二叉树 力扣 | 思路:反转就是交换左右两个节点的位置,如果是根节点就不用交换,交换root.left 和 root.right 节点,之后递归去反转根节点的左子树的左子树,右子树的右子树。 |
4. 判断一颗二叉树是否为平衡二叉树( 分别在O(N*2)和O(N)的时间复杂度代码来写 ) 力扣 | 1. 思路:相邻的左右两个节点高度差如果超过1,就不是平衡,否则就是平衡树。(求高度的过程要写成一个方法) 2. 思路:在求高度的过程中就判断高度差是否超过1,如果高度差超过1,此时就返回一个-1,如果求高度过程中返回了-1,之后的节点就不用求高度了,时间复杂度就是O(N) |
5. 对称二叉树 力扣 | 思路:判断整棵树是否对称,需要判断这棵树的左子树和右子树是否是对称的,和判断是否为相同的树类似,只是判断的节点换成了左子树的左和右子树的右是否相同。 |
6. 二叉树的构建及遍历(根据先序遍历创建一颗二叉树) 二叉树遍历_牛客题霸_牛客网 | 思路:在遍历字符串的过程中,创建节点并且递归创建左子树和右子树,之后按中序遍历进行输出即可。 |
7. 二叉树的层序遍历 力扣 | 思路:层序遍历是有顺序的,此时需要用合适的数据结构:队列,先入队列根,之后在弹出节点的时候进行记录,左右不为空的情况就把左和右子节点入队列。 |
8. 二叉树中两个指定节点的最近公共祖先 力扣 | 思路:如果在根的两边(p在左子树,q在右子树),此时根节点就是,如果都在左边,就去遍历二叉树,找到一个节点就返回(先找到的节点就是公共祖先),如果都在右边也是同理。 |
9. 根据前序遍历和中序遍历构造一颗二叉树 力扣 | 思路:先在前序遍历中找到根,然后拿着根在中序遍历 中找到根的位置,根的左边就是左子树,根的右边就是右子树,(记录左子树和右子树的下标)然后根据左子树和右子树的下标递归创建左树和右树。 |
10. 根据后序遍历和中序遍历构建一颗二叉树 力扣 | 思路:在后序遍历中找到根的位置,然后再在中序遍历中找到根的位置,划分左子树,右子树,记录左子树和右子树的下标,根据下标递归创建左树和右树。 |
11. 二叉树创建字符串 力扣 | 思路:考虑几种情况;左子树为空的前提下,右子树为空或者不为空,左子树不为空的前提下,右子树为空或者不为空。 |
12. 二叉树的前序 非递归遍历 力扣 | 思路:用栈这个数据结构,定义一个cur节点,当cur.left不为空的时候,就一直往左走(同时入栈走过的节点),一直到cur为空了,此时弹出栈顶节点,打印弹出的节点,同时记录这个节点,然后让cur走到弹出节点的右边,继续遍历,直到栈空了,此时也就遍历完成了。 |
13. 二叉树的中序 非递归遍历 力扣 | 思路:和前序遍历类似,只是打印的时机不同了。 |
14. 二叉树的后序 非递归遍历 力扣 | 思路:和前中序遍历类似,只是需要注意两点:(1)需要判断根以下的右子树是否为空(两种情况代码不一样) (2)在记录的节点的右子节点打印之后就不要再次进行打印了。 |
oj题代码详解:
//二叉树的构建及遍历:读入一颗先序遍历的字符串,创建一颗二叉树
//然后按中序遍历输出二叉树的节点
//虽然只是一个前序遍历的字符串,但是也是可以创建出一颗二叉树的(有顺序的前序遍历)
/*此处的字符串下标是不会越界的,因为给的前序遍历本来就是一个合法的字符串,如果多给了
* 或者是少给了,此时在创建右树的时候就会发生越界,因为字符串已经遍历完了,但是可能树
* 还没有建完,所以还会递归,但是现在是合法的字符串,此时递归的时候有回退的次数*/
public static void main(String[] args) {
//在main方法中将i置零也是可以的,
Scanner scan = new Scanner(System.in);
//将字符串整行都读进来
String str = scan.nextLine();
TreeNode root = createTree(str);
inorder(root);
}
public static int i = 0;
public static TreeNode createTree(String str) {
TreeNode root = null;
char ch = str.charAt(i);
if (ch != '#') {
root = new TreeNode(ch);
i++;
root.left = createTree(str);
root.right = createTree(str);
}else {
i++;
}
return root;
}
public static void inorder(TreeNode root) {
if (root == null) return;
inorder(root.left);
System.out.println(root.val + " ");
inorder(root.right);
}
//二叉树的最近公共祖先
/*1.在根的两边 2.要么都在根的左边或者右边(其中一个就是公共祖先)*/
public TreeNode lowestCommonAncestor(
TreeNode root, TreeNode p, TreeNode q) {
if (root == null) return null;
if (root == p || root == q) return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if (left != null && right != null) return root;
/*这个地方是找到就返回了,如:在左边先找到了一个节点,此时p和q都在
* root的左边,但是找到p就结束了,不会再去找另一个节点了,所以返回的
* 节点就是上边的节点,就是最近的公共祖先*/
else if (left != null) return left;
else if (right != null) return right;
else return null;
}
//如果每个节点有了父亲节点的地址,此时就变成了求相交节点
//但是二叉树没有父亲节点,所以用一个数据结构:栈
/*把找p和q的路径入到两个栈中,然后元素多的先出差值个元素,之后再一起出
* 如果元素相等此时这个元素就是最近公共祖先*/
//找到从根节点到指定节点node路径上所有的节点,然后入栈
public boolean getPath(TreeNode root,
TreeNode node, Deque<TreeNode> stack) {
if (root == null || node == null) return false;
stack.push(root);
if (root == node) return true;
boolean ret1 = getPath(root.left,node,stack);
boolean ret2 = getPath(root.right,node,stack);
if (ret1) return true;
if (ret2) return true;
//左边和右边都没找到这个node,此时就回退,让这个元素出栈
stack.pop();
return false;//说明这条路径走不通,走到头了,也没找到这个节点
}
public TreeNode lowestCommonAncestor2(TreeNode root,
TreeNode p, TreeNode q) {
//1.两个栈中先存储好数据
Deque<TreeNode> stack1 = new LinkedList<>();
getPath(root,p,stack1);
Deque<TreeNode> stack2 = new LinkedList<>();
getPath(root,q,stack2);
//2.判断栈的大小,出差值个元素
int size1 = stack1.size();
int size2 = stack2.size();
//让size1是最大的
int ret = Math.abs(size1 - size2);
while (ret != 0) {
if (size1 > size2) {
stack1.pop();
}else {
stack2.pop();
}
ret--;
}
//栈中元素个数相等,此时一块出元素
while (!stack1.isEmpty() && !stack2.isEmpty()) {
if (stack1.peek() != stack2.peek()) {
stack1.pop();
stack2.pop();
}else {
return stack1.pop();
}
}
return null;
}
//根据前序遍历和中序遍历构造一颗二叉树
/*1.根据前序遍历找到根 2.在中序遍历中找到根的位置*/
//public int i = 0;
public TreeNode buildTree(int[] preorder, int[] inorder) {
TreeNode root = buildTreeChild(preorder, inorder, 0,
inorder.length - 1);
return root;
}
public TreeNode buildTreeChild(int[] preorder, int[] inorder,
int begin, int end) {
if (begin > end) return null;//如果下标越界,此时说明没有节点了
//TreeNode root = new TreeNode(preorder[i]);
//找到当前根在中序遍历中的位置
int rootIndex = findIndex(inorder,begin, end, preorder[i]);
i++;
root.left = buildTreeChild(preorder,inorder,begin,rootIndex-1);
root.right = buildTreeChild(preorder, inorder, rootIndex+1,end);
return root;
}
private int findIndex(int[] inorder, int begin, int end, int key) {
for (int j = begin; j <= end; j++) {
if (key == inorder[j]) return j;
}
return -1;
}
//根据中序遍历和后序遍历来创建一颗二叉树
/*1.先从后续遍历中找到根,之后在中序遍历中找到根的位置*/
/*然后i--,要注意,先创建的是右树,然后创建左树*/
public int a;
public TreeNode buildTree3(int[] inorder, int[] postorder) {
a = postorder.length - 1;
TreeNode root = buildChildTree(inorder,postorder,
0, inorder.length - 1);
return root;
}
public TreeNode buildChildTree(int[] inorder,int[] postorder,
int begin, int end) {
//TreeNode root = new TreeNode(postorder[a]);
int rootIndex = findIndex(inorder, begin, end, postorder[a]);
a--;
root.right = buildChildTree(inorder,postorder,rootIndex + 1,end);
root.left = buildChildTree(inorder, postorder, begin, rootIndex - 1);
return root;
}
//根据二叉树创建字符串
/*要以前序遍历的方式来创建这个字符串*/
public String tree2str(TreeNode root) {
if (root == null) return null;
StringBuilder builder = new StringBuilder();
tree2strChild(root, builder);
/*1.左边为空,右边为空 2.左边不为空右边为空 3.左边为空右边不为空*/
return builder.toString();
}
public void tree2strChild(TreeNode root, StringBuilder builder) {
if (root == null) return;
builder.append(root.val);
//左子树为空或者不为空
if (root.left != null) {
builder.append("(");
tree2strChild(root.left,builder);
builder.append(")");
}else {
//左边为空的情况下考虑右边
if (root.right != null) {
builder.append("()");
}else {
return;
}
}
//右子树为空或者不为空
if (root.right != null) {
builder.append("(");
tree2strChild(root.right,builder);
builder.append(")");
}else {
return;
}
}
//判断一棵树是否为完全二叉树
//用合适的数据结构: 队列
/*每次从队列中取出一个节点,不为空:把左子树和右子树带进来,
* 为空:开始判断队列中剩余的元素*/
public boolean isCompleteTree(TreeNode root) {
if (root == null) return true;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode cur = queue.poll();
if (cur != null) {
queue.offer(cur.left);
queue.offer(cur.right);
}else {
//如果cur为空说明左和右都是空的了,此时就去判断队列中的元素是否都是空的
break;
}
}
while (!queue.isEmpty()) {
TreeNode tmp = queue.poll();
if (tmp != null) return false;
}
return true;
}
//非递归实现前序遍历
public List<Integer> preorderTraversalNor(TreeNode root) {
List<Integer> list = new ArrayList<>();
TreeNode cur = root;
Stack<TreeNode> stack = new Stack<>();
while (cur != null || !stack.isEmpty()) {
while (cur != null) {
stack.push(cur);
list.add(cur.val);
cur = cur.left;
}
TreeNode top = stack.pop();
cur = top.right;
}
return list;
}
//非递归实现中序遍历
public List<Integer> inorderTraversalNor(TreeNode root) {
List<Integer> list = new ArrayList<>();
TreeNode cur = root;
Stack<TreeNode> stack = new Stack<>();
while (cur != null || !stack.isEmpty()) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
TreeNode top = stack.pop();
list.add(top.val);
cur = top.right;
}
return list;
}
//非递归实现后序遍历
public List<Integer> postorderTraversalNor(TreeNode root) {
List<Integer> list = new ArrayList<>();
TreeNode cur = root;
Stack<TreeNode> stack = new Stack<>();
TreeNode prev = null;
while (cur != null || !stack.isEmpty()) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
TreeNode top = stack.peek();
//此时需要注意:当打印之后top.right之后就不要再次打印了
//所以prev记录的是 是否打印过top.right这个节点
if (top.right == null || prev == top.right) {
stack.pop();
list.add(top.val);
prev = top;
}else {
cur = top.right;
}
}
return list;
}






![[进阶]TCP通信综合案例:群聊](https://img-blog.csdnimg.cn/fc6b9178cfaa4c17a72c7fa21b048ebd.png)