目录

✿LeetCode104.二叉树的最大深度❀

✿LeetCode559.n叉树的最大深度❀

✿LeetCode111.二叉树的最小深度❀ 

✿LeetCode222.完全二叉树的节点个数❀

---

✿LeetCode104.二叉树的最大深度❀

链接：104.二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

 

 可以用后序遍历，也可以用前序遍历，后序遍历求的是高度，前序遍历求的是深度，在此题中两个是一样的，递归的代码如下：

public int maxDepth(TreeNode root) {
        return getHeight(root);
    }
    public int getHeight(TreeNode root){
       //后序遍历  求高度
        if(root==null){
            return 0;
        }
        int leftH=getHeight(root.left);
        int rightH=getHeight(root.right);
        int height=1+Math.max(leftH,rightH);
        return height;
    }

 int result=0;
    public int maxDepth(TreeNode root) {
        result=0;
        if(root==null){
            return 0;
        }
        return getDepth(root,1);
    }
    public int getDepth(TreeNode root,int depth){
        // 前序遍历  求深度
        result=Math.max(result,depth);
        if(root.left==null && root.right==null){
            return result;
        }
        if(root.left!=null){
            depth++;
            getDepth(root.left,depth);
            depth--;
        }
        if(root.right!=null){
            depth++;
            getDepth(root.right,depth);
            depth--;
        }
        return result;
    }

此外，还有迭代法，用层序遍历来实现，遍历完每一层，深度++，代码如下： 

public int maxDepth(TreeNode root) {
        // 迭代法
        // 层序遍历
        if(root==null){
            return 0;
        }
        Queue<TreeNode> qu=new LinkedList<>();
        qu.offer(root);
        int depth=0;
        while(!qu.isEmpty()){
            int size=qu.size();
            depth++;
            while(size>0){
                TreeNode node=qu.poll();
                if(node.left!=null){
                    qu.offer(node.left);
                }
                if(node.right!=null){
                    qu.offer(node.right);
                }
                size--;
            }
        }
        return depth;
    }

✿LeetCode559.n叉树的最大深度❀

链接：559.n叉树的最大深度

 给定一个 N 叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔（请参见示例）。

 

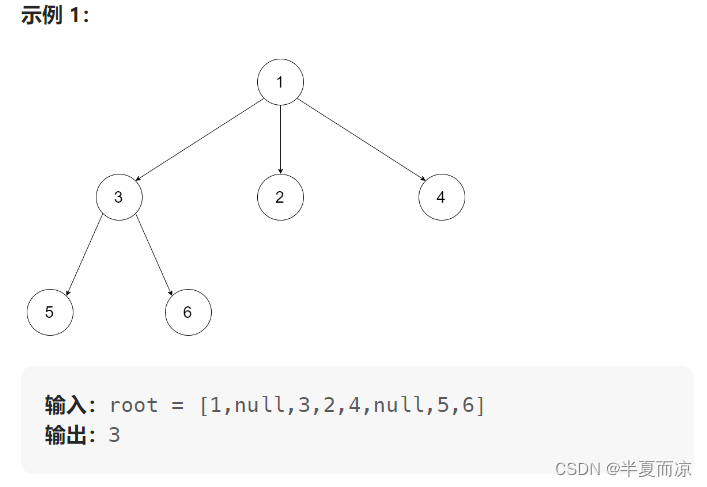
n叉树和二叉树的唯一不同就是n叉树有多个子节点，n叉树的定义如下： 

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/

具体代码实现，思路还是一样的，代码如下： 

public int maxDepth(Node root) {
      //递归
        int depth=0;
        if(root==null){
            return 0;
        }
        if(root.children!=null){
            for(Node child: root.children){
                depth=Math.max(depth,maxDepth(child));
            }
        }
        return depth+1;
    }

 public int maxDepth(Node root) {
        // 迭代法
        if(root==null){
            return 0;
        }
        Queue<Node> qu=new LinkedList<>();
        qu.offer(root);
        int depth=0;
        while(!qu.isEmpty()){
            int size=qu.size();
            depth++;
            while(size>0){
                Node node=qu.poll();
                if(node!=null){
                    for(int i=0;i<node.children.size();i++){
                        qu.offer(node.children.get(i));
                    }
                }
                size--;
            }
        }
        return depth;
    }

✿LeetCode111.二叉树的最小深度❀ 

链接：111.二叉树的最小深度

 给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

 

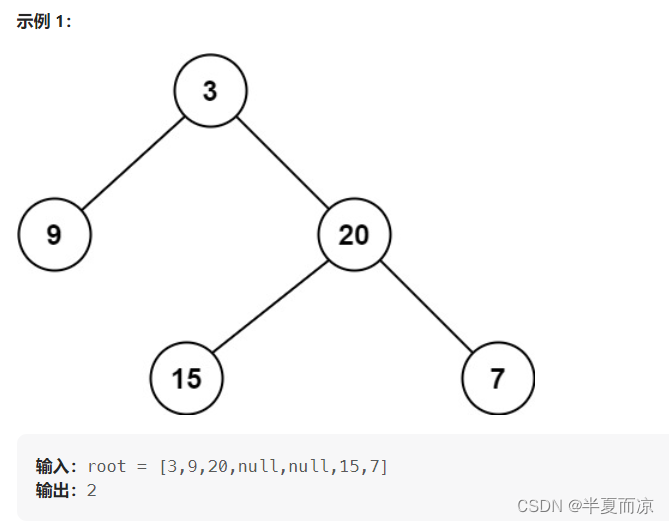
求最小深度和求最大深度还是有点不一样的，如果根节点没有左节点，但是有右节点，最小深度不是1，而是根节点到最近叶子节点的最短路径上的节点数量。代码如下：

public int minDepth(TreeNode root) {
        if(root==null){
            return 0;
        }
        int leftD=minDepth(root.left);
        int rightD=minDepth(root.right);
        if(root.left==null){
            return rightD+1;
        }
        if(root.right==null){
            return leftD+1;
        }
        return 1+Math.min(rightD,leftD);
    }

public int minDepth(TreeNode root) {
        // 迭代法
        // 层序遍历
        if(root==null){
            return 0;
        }
        Queue<TreeNode> qu=new LinkedList<>();
        qu.offer(root);
        int depth=0;
        while(!qu.isEmpty()){
            int size=qu.size();
            depth++;
            while(size>0){
                TreeNode node=qu.poll();
                if(node.left==null && node.right==null){
                    return depth;   //到达叶子结点
                }
                if(node.left!=null){
                    qu.offer(node.left);
                }
                if(node.right!=null){
                    qu.offer(node.right);
                }
                size--;
            }
        }
        return depth;
    }

✿LeetCode222.完全二叉树的节点个数❀

链接：222.完全二叉树的节点个数

 给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

 

 

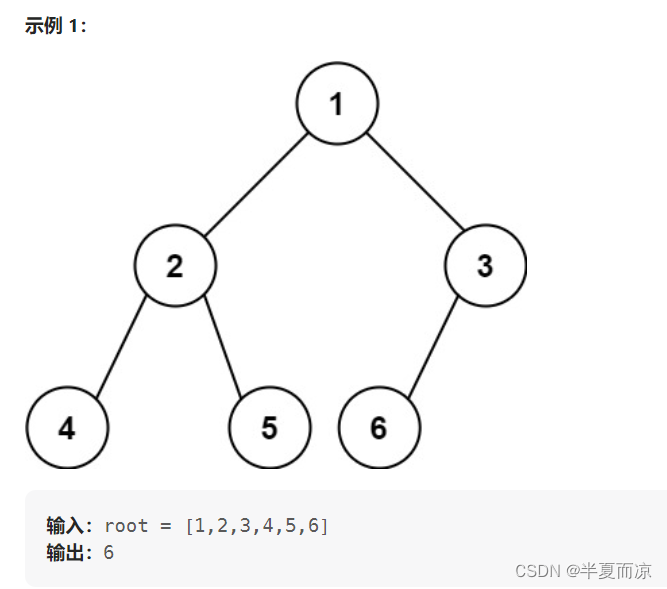
// 迭代法
    public int countNodes(TreeNode root) {
        if (root == null) return 0;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int result = 0;
        while (!queue.isEmpty()) {
            int size = queue.size();
            while (size -- > 0) {
                TreeNode cur = queue.poll();
                result++;
                if (cur.left != null) queue.offer(cur.left);
                if (cur.right != null) queue.offer(cur.right);
            }
        }
        return result;
    }

public int countNodes(TreeNode root) {
       //递归法
        if(root==null){
            return 0;
        }
        int leftnum=countNodes(root.left);
        int rightnum=countNodes(root.right);
        return leftnum+rightnum+1;
    }