| 实验目的: 1.掌握因子分析的基本思想; 2.熟悉掌握SPSS软件进行因子分析的基本操作; 3.利用实验指导的实例数据,上机熟悉因子分析方法。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 实验内容: 附表的数据来自一次对液晶电视的调查。在这次调查中,被调查者回答了关于电视机音响效果、画面清晰度、画面色彩、外观效果、性价比和操作方便性等几个方面对于购买决策是否重要的问题。如果被调查者认为自己在购买电视机时非常注重某个方面,则打5分,比较注重打4分,注重程度一般打3分,不太注重打2分,非常不注重打1分。下面的数据适合做因子分析吗?如果适合,请进行因子分析,并对分析的结果进行解释。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 实验前预习: 主成分分析的基本思想; SPSS软件进行主成分分析的基本操作; | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 程序测试、运行结果及分析: 因子分析操作步骤: 打开spss软件,输入相关数据 à 在“变量视图”更改名称 à 点击“分析”à 点击“描述统计” à 选择“描述” à 点击“将标准化数值另存为变量”并点击“确定”à点击“分析”à点击“降维” à 选择“因子分析”à拖动标准化后的变量拖至变量框 à 点击“描述”选择KMO和“系数”à点击提取选择“主成分”和“碎石图”à 点击旋转选择“最大方差法”à 点击得分选择“保存为变量”à 点击“继续”和“确定” 运行结果及分析:
X1,X2,X3、X4、X5、X6,分别代表、画面清晰度、 给出相关系数矩阵,可以看出,一些变量的相关程度较小。
0.575较小,可能得出的的因子分析模型不太理想,0.00表示各个变量存在相关性。
提取列数据表示为公共因子解释其余变量的方差的比例,即各变量含有原始变量的信息能被提取的公因子代表程度,0.123说明提取的公因子对该变量的代表性是很差的。
表明各因子的方差贡献率和累计贡献率。
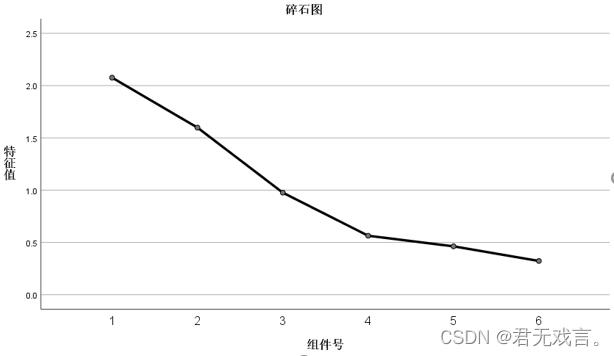
特征值反应变量的重要程度。
结果表示第一个因子在音响效果和画面色彩以及外观效果上有较大的载荷,因此第一个因子为电视机的性能效果因子。而第二个因子在性价比和操作方便上有较大载荷,所以第二个因子为电视机的实用性效果因子。 最终得到公式:X1=0.863*F1+0.068*F2,X1=-0.263*F1+0.232*F2….. 主成分中是按列写出各个主成分公式,但是在因子分析中是按行看,表示各因子在各变量上的载荷(各因子对各变量的影响程度)
由得分系数矩阵可知: F1=0.416*x1-0.131*x2+0.376*x3+0.378*x4+0.069*x5-0.062*x6, F2略。 软件自动保存变量,数据视图中给出了各因子得分,默认变量名为FAC1_1、FAC2_1、FAC3_1。在数字表达式中输入34.483 / 61.240*FAC1_1+26.757/61.240*FAC2_1得到结果后右键数据列选择降序排序得到表格:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 讨论: 1.主成分分析和因子分析的区别 (1)因子分析需要构造因子模型,着重要求新变量,具有实际的意义,能解释原始变量间的内在结构。 (2)主成分分析仅仅是变量变换,是原始变量的线性组合表示新的综合变量,强调新变量贡献了多大比例的方差,不关心新变量是否有明确的实际意义。两者都是降维和信息浓缩的方法,生成的新变量均代表了原始变量的大部分信息且互相独立,都可以用于后续的回归分析、判别分析、聚类分析等等。 2.主成分分析和因子分析的基本原理 主成分分析基本原理:利用降维(线性变换)的思想,在损失很少信息的前提下把多个指标转化为几个不相关的综合指标(主成分),即每个主成分都是原始变量的线性组合,且各个主成分之间互不相关,使得主成分比原始变量具有某些更优越的性能(主成分必须保留原始变量90%以上的信息),从而达到简化系统结构,抓住问题实质的目的。 因子分析基本原理:利用降维的思想,由研究原始变量相关矩阵内部的依赖关系出发,把一些具有错综复杂关系的变量表示成少数的公共因子和仅对某一个变量有作用的特殊因子线性组合而成。就是要从数据中提取对变量起解释作用的少数公共因子(因子分析是主成分的推广,相对于主成分分析,更倾向于描述原始变量之间的相关关系)。 2.总结 因子分析就是研究如何以最少的信息丢失将众多原有变量浓缩成少数几个因子,以较少几个因子来反映原始变量的大部分信息的统计学分析方法。它的基本思想是将原始变量分类,将相关性较高的变量分在同一类,而不同类的变量之间相关性较低,那么每一类变量实际上就代表了一个基本结构,即公共因子。 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
基于spss的多元统计分析 之 因子分析(4/8)
news2026/2/13 8:49:55
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/673513.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
English Learning - L3 作业打卡 Lesson7 Day48 2023.6.21 周三
English Learning - L3 作业打卡 Lesson7 Day48 2023.6.21 周三 引言🍉句1: I thought the worst was over until weeks later when I saw my new legs for the first time.成分划分弱读连读爆破语调 🍉句2: I didn’t know what to expect but I wasn‘…
【C++】 Qt-认识Qt
文章目录 Qt简介Qt建立工程准备建立控制台程序建立桌面窗口程序 Qt简介
Qt(官方发音[kju:t],同音cute)是一个跨平台的C开发库,主要用来开发图形用户界面(Graphical User Interface,GUI)程序&am…
Android之 日历单选多选控件
一,效果图
1.1 单选 2.2 多选 二 实现思路
2.1 数据来源,利用原生日历Calendar,获取从本月开始的往后一年的日期,遍历月数添加全部天数据
private void initCalendarData() {Calendar calendar Calendar.getInstance();year …
Chrome(Manifest Version 3) 浏览器扩展插件基础教程
文章目录 一、简介二、核心介绍三、自定义页面背景色三、设置页面背景图(web_accessible_resources)四、设置徽章(Badge)五、桌面通知六、消息通信七、自定义右键菜单(添加、更新、删除)八、Omnibox九、浏览…
云原生监控平台 Prometheus 的相关概念及部署
1 Prometheus简介 Prometheus 是一个开源的系统监控和报警系统,在 2012 年由 SoundCloud 公司创建,并于 2015 年正式发布。2016 年,Prometheus 正式加入 CNCF (Cloud Native Computing Foundation),成为继kubernetes之后第二个在C…
Redis---集群
目录
一、集群的介绍
1.1 为什么需要集群呢? 1.2 什么是集群?
1.2 集群能干什么呢?
二、集群的算法之分片&槽位slot
2.1 什么是槽位slot? 2.2 分片 2.3 使用槽位和分片的优势 2.4 slot 槽位映射的三种算法
1、哈…
postgresql 从应用角度看快照snapshot使用,事务隔离控制不再神密
专栏内容:postgresql内核源码分析 个人主页:我的主页 座右铭:天行健,君子以自强不息;地势坤,君子以厚德载物. 快照使用 快照是事务中使用,配合事务的隔离级别,体现出不同的可见性。…
端午节粽子(python)
目录 前言
正文 粽叶绘制
粽叶绳绘制
祝福语绘制
源代码 总结 前言
今天端午节,然后昨天也学习一下绘图的相关知识,然后就想看一下能不能画一下,结果还是有点困难的,用CharAI生成简直一言难尽了。后面是找了一个改了一下。
…
MicroBlaze Processor hello world实验
MicroBlaze Processor hello world实验
实验目的
搭建microblaze工程,通过串口打印hello world,了解microblaze的使用,加深对FPGA硬件和软件开发的理解。
实验原理 MicroBlaze Processor是xilinx提供的一个软核处理器(使用FPGA…
Delta型腿机器狗全动作展示
1. 功能说明 本文示例将实现R322样机Delta型腿机器狗维持身体平衡、原地圆形摆动、原地踏步、蹲起、站立、前进、后退、转向、横向移动、斜向移动等功能。 2. 电子硬件 本实验中采用了以下硬件:
主控板 Basra主控板(兼容Arduino Uno) 扩展…
追寻技术巅峰:开发者的端午征途
近年来,随着信息技术的飞速发展,开发者们以前所未有的速度和规模推动着技术的进步。而正如端午节的文化内涵所体现的那样,我们以屈原名言为指引,勉励着广大开发者在技术征途上不断追求极致,勇往直前。 一、端午节与技术…
macOS Sonoma 14 beta 2 (23A5276g) Boot ISO 原版可引导镜像
macOS Sonoma 14 beta 2 (23A5276g) Boot ISO 原版可引导镜像
本站下载的 macOS 软件包,既可以拖拽到 Applications(应用程序)下直接安装,也可以制作启动 U 盘安装,或者在虚拟机中启动安装。另外也支持在 Windows 和 …
【Flume】高级组件之Sink Processors及项目实践(Sink负载均衡和故障转移)
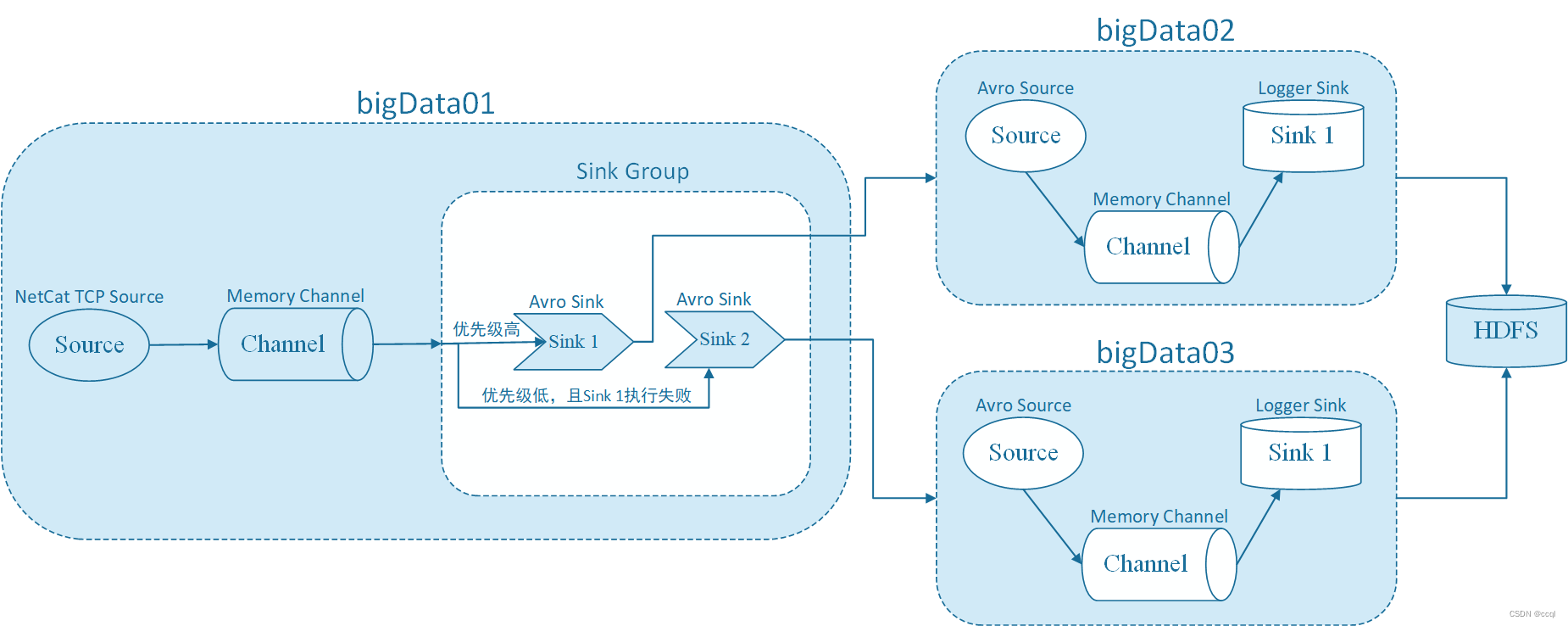
文章目录 1. 组件简介2. 项目实践2.1 负载均衡2.1.1 需求2.1.2 配置2.1.3 运行 2.2 故障转移2.2.1 需求2.2.2 配置2.2.3 运行 1. 组件简介 Sink Processors类型包括这三种:Default Sink Processor、Load balancing Sink Processor和Failover Sink Processor。
Defa…
AIGC连续内容生成几种方案
背景
从AI可以画图到现在各家都在功课的连续性内容的输出,正在AI画图进入到大众圈其实也不过1年左右时间。对于单图的研究已经逐渐完善,单图理论上讲,只要你能按要求做promt的设计出图率应该是比较高的。但是对于要生成连续的图或者要生成连…
推荐 5 个 火火火 的 GitHub 项目
推荐 5 个开源项目,前两个是 AI 相关,后面 3 个为逛逛GitHub 的读者推荐,如果你挖掘到了很棒的开源项目,可以给老逛投稿。 本期推荐开源项目目录: 1. SuperAGI(AI) 2. 一键换脸(AI&a…
macOS Monterey 12.6.7 (21G651) Boot ISO 原版可引导镜像
macOS Monterey 12.6.7 (21G651) Boot ISO 原版可引导镜像
本站下载的 macOS 软件包,既可以拖拽到 Applications(应用程序)下直接安装,也可以制作启动 U 盘安装,或者在虚拟机中启动安装。另外也支持在 Windows 和 Lin…
计算机实习自我鉴定范文5篇
精选计算机实习鉴定 (一) 时间过的真快,在这过去一个3个月时间里,我在**科技有限公司实习从事运维工作。 在公司实习的这段时间,我主要和其他的实习生一起负责公司刚开发的**系统的部署、更新以及维护。 这三月的时间,在同事和项目…
【并发知识点】CAS的实现原理及应用
系列文章目录
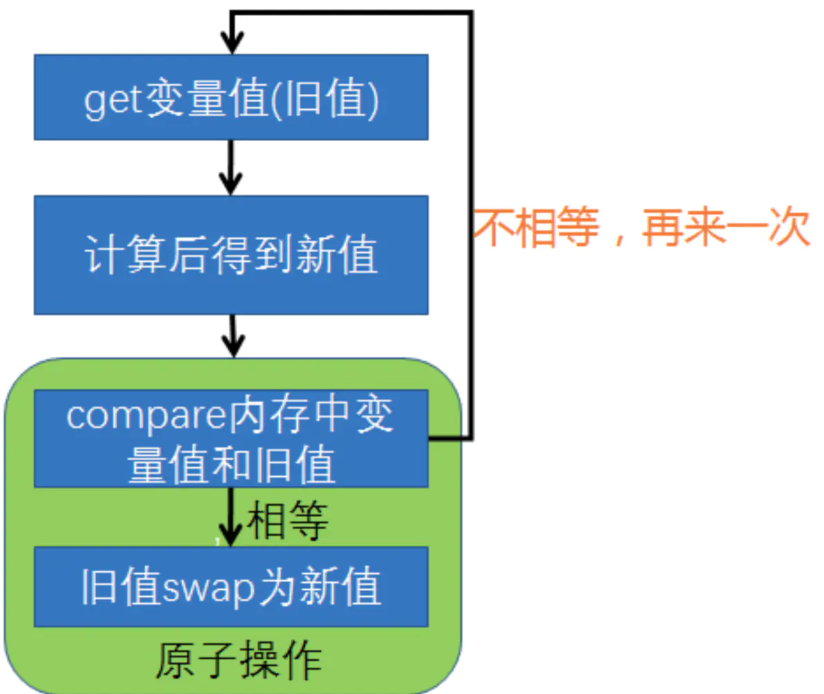
AQS的实现原理及应用 CAS的实现原理及应用 文章目录 系列文章目录前言1、CAS的概念2、CAS的实现原理3、单JVM内锁CAS实现3.1、效果 4、模拟赛龙舟比赛 前言
本章节介绍CAS概念、实现原理,并通过java代码应用,最终模拟赛龙舟比赛。
1、CA…
设计模式之适配器模式笔记
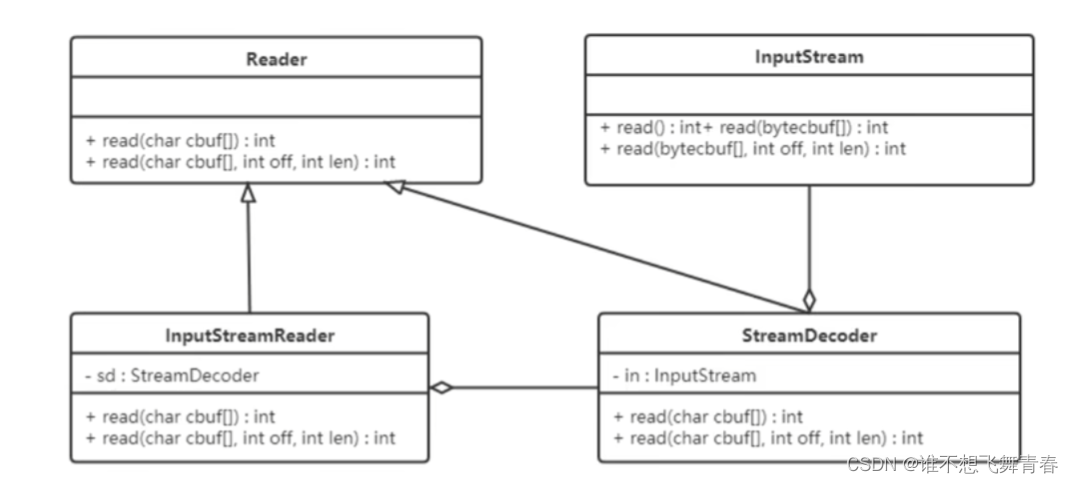
设计模式之适配器模式笔记 说明Adapter(适配器)目录类适配器模式示例类图适配者类的接口适配者类目标接口具体的SD卡类计算机类适配器类测试类 对象适配器模式适配者类的接口适配者类目标接口具体的SD卡类计算机类适配器类测试类 说明
记录下学习设计模式-适配器模式的写法。J…