二叉树的遍历

•二叉树的遍历定义

​ • 按照一定次序访问树中所有节点,并且每个节点仅被访问一次的过程.

​ • 遍历是最基本的运算,是树中所有其他运算的基础.

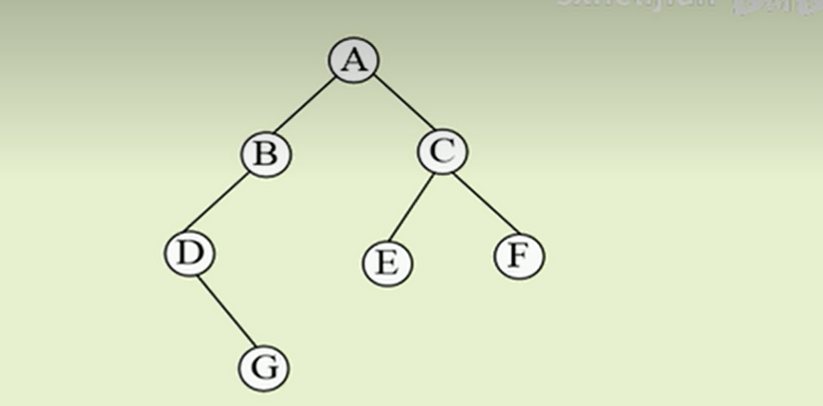
• 二叉树的三种遍历方式

​ • 先序遍历:

​ 根节点–>左子树–>右子树 : ABDGCEF

​ • 中序遍历:

​ 左子树–>根节点–>右子树 : DGBAECF

​ • 后序遍历:

​ 左子树–>右子树–>根节点 : GDBEFCA

先序遍历的递归算法

▪ 先序遍历二叉树的过程

​ •访问根节点

​ • 先序遍历左子树

​ • 先序遍历右子树

构建思路 :

先遍历根节点 , 然后再遍历其左子树和右子树,这是一个层级,把其左子树或右子树再次当做一个独立的树去调用(每个节点被传入调用的时候,都当了一次根节点,所以才有机会被输出),目的就是输出访问一遍,

代码实现:

//传入要遍历的树的根节点
void PreOrder(BTNode *b)
{
	//先判断传入的根节点是否为空,为空则无操作
    if(b!=NULL)
    {
        //根节点不为空,就先输出根节点
    	printf("%c",b->data);
        //然后输出左子树和右子树
        PreOrder(b->lchild);
        PreOrder(b->rchild);        
    }        
}    

中序和后序遍历的递归算法

● 中序遍历二叉树的过程

​ • 中序遍历左子树

​ • 访问根节点

​ • 中序遍历右子树

思路: 都差不多,都是在同一层级上进行递归调用,我们换一下顺序即可

代码实现:

//传入要遍历的树的根节点
void PreOrder(BTNode *b)
{
	//先判断传入的根节点是否为空,为空则无操作
    if(b!=NULL)
    {
        //先输出左子树
         PreOrder(b->lchild);
        //然后输出根节点
    	printf("%c",b->data);
        //最后输出右子树
        PreOrder(b->rchild);        
    }        
}  

● 后序遍历二叉树的过程

​ • 后序遍历左子树

​ • 后序遍历右子树

​ • 访问根节点

代码实现:

//传入要遍历的树的根节点
void PreOrder(BTNode *b)
{
	//先判断传入的根节点是否为空,为空则无操作
    if(b!=NULL)
    {
        //先输出左子树
        PreOrder(b->lchild);
        //然后输出右子树
        PreOrder(b->rchild); 
		//最后输出根节点
    	printf("%c",b->data);
    }        
}  

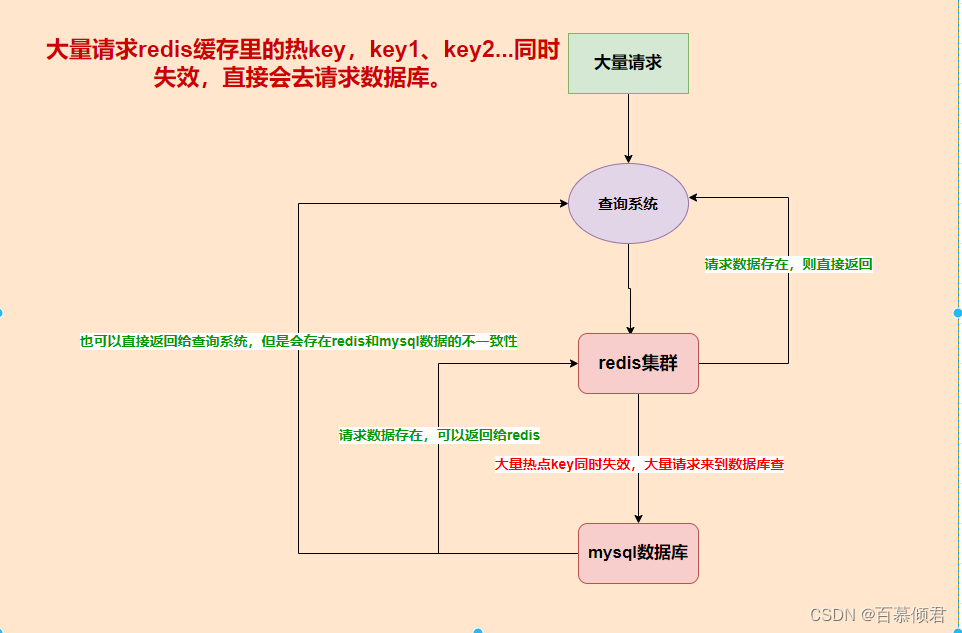
二叉树遍历的相关问题

♥问题1

​ • 假设二叉树采用二叉链式存储 ,设计算法,计算一棵给定二叉树的所有节点个数

解题模型

​ •解:计算一棵二叉树b中所有节点个数的递归模型f(b)如下:

​

▪算法构思:

我们既然要算二叉树有几个节点,不如就把每个节点都访问一遍, 那怎么去访问呢? 当然是一层一层的去访问, 所以我们需要在同一层级上进行规划好,剩下的交给代码调用自身, 去返回每一层的值即可.当我们把一个层级的所有情况处理完, 那当再去调用处理其他层级的子树的时候, 我们就可以游刃有余了.

▪代码实现:

//传入要计算的二叉树的根节点
int Nodes(BTNode *b)
{
    //如果传入的根节点为空,则说明无节点,返回0
	if(b==NULL)
    {
    	return 0;
    }
//否则就说明起码有一个节点, 此时我们需要考虑根节点的左右子树的个数,左右子树节点个数总和加一就是我们所要求的传入的二叉树的节点个数
	else
    {
        //调用左子树和右子树,然后返回其节点个数,其和加一就是二叉树节点个数
    	return (Nodes(b->lchild)+Nodes(b->rchild)+1);
    }
}    

♥问题2

​ • 假设二叉树采用二叉链式存储结构存储,试设计一个算法输出一棵给定二叉树的所有叶子节点

解题模型

♥解:输出一棵二叉树的所有叶子节点的递归模型f()如下

​ • 不做任何事情 若b = NULl

​ • 输出*b节点的data域 若 *b 为叶子节点

​ • f(b->lchild);f(b->rchild) 其他情况

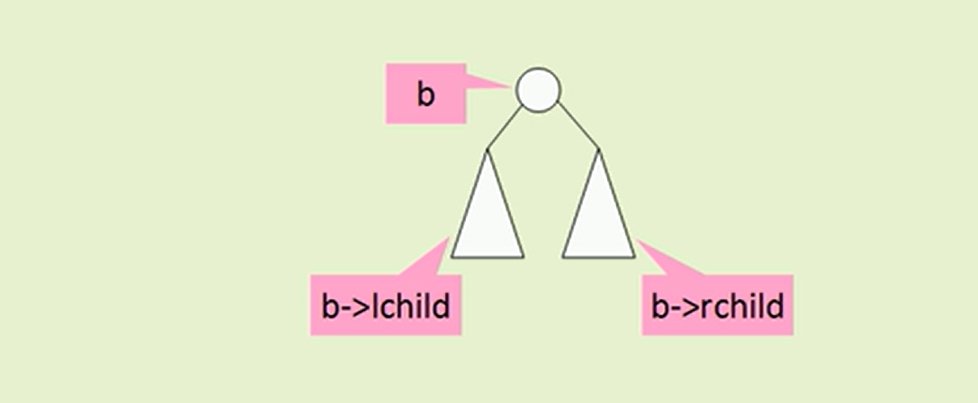
构建思路:

当我们要输出一棵二叉树的时候,我们先采用根左右的方式 , 这样容易处理,

①当传入的根节点为空时候,那就不处理

②当传入的根节点不为空的时候,什么时候输出这个根节点呢?

就是当此根节点就是叶子节点, 就将其输出

③当此根节点还有孩子的时候,说明其不是叶子节点,我们接着往下递归遍历即可

​ (1)把其左子树的叶子节点输出

​ (2)把其右子树的叶子节点输出

代码如下:

//传入树的根节点
void DispLeaf(BTNode *b)
{
	//当其不为空时,接着往下走,看其后面有没有叶子节点
    if(b!=NULL)
    {
    	//如果此根节点没有孩子,说明其就是叶子节点,输出其数据域即可
        if(b->lchild==NULL && b->rchild == NULL)
        {
        	printf("%c,b->data");
        }   
        //不是叶子节点就说明其有孩子,输出其孩子的叶子节点即可
        else
        {
        	DispLeaf(b->lchild);
        	DispLeaf(b->rchild);            
        }
    }      
}  

♥问题3

二叉树(没有值相同的节点)采用二叉链式存储结构,设计一个算法Level(b,x,h),

返回二叉链b中data值为x的节点的层数.

算法构思:

我们既然要遍历二叉树特定节点的层数, 就需要遍历所有节点, 所以我们要定义遍历节点的指针*b,

传入寻找的值, 并且还需要定义一个存储当前对比到的节点的层数h

然后我们采用先序遍历, 先在同一层级进行遍历操作 ,

• 如果传入的根节点为空,则返回0

• 如果传入的根节点就是所找的节点, 就返回此时的层数 h

• 如果上述两种情况都不符合, 就接着看其左右孩子中是否有所找的节点

注意: 我们每次传入子树的时候, 就需要在此层级的层数h基础上加一,表示深度加一,到了下一个层级

代码构建:

//传入要对比的二叉树的根节点的指针,要寻找的节点,此时正在遍历的节点的层数
//注意:此时 *b 里面存储的是正在进行遍历对比的节点
int Level(BTNode *b,ElemType x,int h)
{
    //定义子树的深度
    int I = 0;
	//如果传入的节点为空,就返回0
    if(b==NULL)
    {
    	return 0;
    }        
    //如果传入的节点的不为空,其数据域符合要找的节点就返回其层数
    else if(b->data==x)
    {
		return h;
    }        
    //上两种情况不符合,就判定其有孩子,判断其左右孩子是否存在要找的节点
    else
    {
        //先找其左子树,是否有所要找的节点,然后记录其深度
		I=Level(b->lchild,x,h+1);
        //如果找不到,那每次调用就返回0,接着找右子树
        if(I==0)
        {
            //调用右子树,找到找不到都会返回,无所谓了
        	return Level(b->rchild,x,h+1);
        }
        //不为0就说明找到了
        else
        {
        	return I;
        }                     
    }        
}    
//主函数调用
int main()
{
    //定义构造的二叉树
	BTNode *b;
    //定义层数
    int h;
    //定义要找的特定节点
    ElemType x;
    //构造二叉树
    CreateBTNode(b,"A(B(D(,G)),C(E,F))");
    //输入要找的节点
    scanf("%c",&x);
    //得出调用特定节点的层数
    h = Level(b,x,1);
//    ....
}    

♥问题4

设计一个算法判断两颗二叉树是否相似

算法思路:

​ • 所谓二叉树 t1 和 t2 相似

​ ①t1和t2都是空二叉树,相似;

​ ②t1和t2其中只有一个为空,肯定不相似;

​ ③两个树都不为空,就要对比其子树了—t1的左子树和 t2的左子树是否相似,

​ t1的右子树和 t2的右子树是否相似 .其左子树和右子树都相似我们才能说明两者相似.

解题模型:

解:判断两颗二叉树是否相似的递归模型f()如下:

​ f(t1,t2)=true 若 t1=t2=NULL

​ f(t1,t2)=false 若t1、t2之一为NULL,另一不为NULL

​ f(t1,t2)=f(t1->lchild,t2->lchild)&&f(t1->rchild,t2->rchild) 其他情况

代码构建:

//传入两个二叉树的根节点指针
int Like(BTNode *b1,BTNode *b2)
{
	//定义存储是否相似的标志位
    int like1,like2;
    //如果都是空,则相当于相似
    if(b1==NULL&&b2==NULL)
    {
    	return 1;
    }        
    //否则如果只有一个空,一个不空,则必然不想似
    else if(b1==NULL||b2==NULL)
    {
    	return 0;
    }        
    //否则就说明其有子树,就对比其左子树和右子树
    else
    {
        //调用对比左子树,返回标志位
        like1=Like(b1->lchild,b2->rchild);
        //调用对比右子树,返回标志位
        like2=Like(b1->rchild,b2->rchild);    
        //对比两个子树是否相等,标志位异或运算
        return (like1 && like2);
    }        
}