目录

题目描述

输入描述

输出描述

用例

题目解析

算法源码

---

题目描述

公司创新实验室正在研究如何最小化资源成本，最大化资源利用率，请你设计算法帮他们解决一个任务混部问题：

有taskNum项任务，每个任务有开始时间（startTime），结束时间（endTime），并行度（parallelism）三个属性，

并行度是指这个任务运行时将会占用的服务器数量，一个服务器在每个时刻可以被任意任务使用但最多被一个任务占用，任务运行完成立即释放（结束时刻不占用）。

任务混部问题是指给定一批任务，让这批任务由同一批服务器承载运行，

请你计算完成这批任务混部最少需要多少服务器，从而最大化控制资源成本。

输入描述

第一行输入为taskNum，表示有taskNum项任务
接下来taskNum行，每行三个整数，表示每个任务的

开始时间（startTime ），结束时间（endTime ），并行度（parallelism）

输出描述

一个整数，表示最少需要的服务器数量

备注

• 1 <= taskNum <= 100000
• 0 <= startTime < endTime <= 50000
• 1 <= parallelism <= 100

用例

输入	3 2 3 1 6 9 2 0 5 1
输出	2
说明	一共有三个任务， 第一个任务在时间区间[2, 3]运行，占用1个服务器， 第二个任务在时间区间[6, 9]运行，占用2个服务器， 第三个任务在时间区间[0, 5]运行，占用1个服务器， 需要最多服务器的时间区间为[2, 3]和[6, 9]，需要2个服务器。

输入	2 3 9 2 4 7 3
输出	5
说明	一共两个任务， 第一个任务在时间区间[3, 9]运行，占用2个服务器， 第二个任务在时间区间[4, 7]运行，占用3个服务器， 需要最多服务器的时间区间为[4, 7]，需要5个服务器。

题目解析

用例1图示如下：

用例2图示如下：

通过上面两个图示，我们可以看出，交集重叠越多的时间段内所需的服务器数越大，即题目所要求的最少服务器数。

我的解题思路如下：

先将任务按照开始时间升序排序，比如用例1，就得到了任务顺序如下：

[ [0,5,1], [2,3,1], [6,9,2] ]

然后，将每个任务的时间段的开始时间点和结束时间点都提取出来放到一个set集合中，即得到

[0,5,2,3,6,9]

然后将集合转为数组，进行升序排序

[0,2,3,5,6,9]

现在我得到了一个升序的关键时间点数组[0,2,3,5,6,9]，以及一个开始时间升序的任务数组[ [0,5,1], [2,3,1], [6,9,2] ]。

现在，建立一个双重for，外层遍历关键时间点数组，每遍历到一个关键时间点kp，就去和每一个任务数组的时间区间比较，看kp在不在对应任务的时间区间（左闭右开，即区间不包含结束时间），如果在，则该时间点的服务器数量 += 该任务所需的服务器数量。

代码如下：

function getResult(arr) {
  // 任务数组按照任务开始时间升序排序
  arr.sort((a, b) => a[0] - b[0]);

  // 将所有的关键时间点存入keyPoints集合中
  let keyPoints = new Set();
  for (let [s, e] of arr) {
    keyPoints.add(s);
    keyPoints.add(e);
  }
    
  // 关键时间点升序排序
  keyPoints = [...keyPoints].sort((a,b) => a-b);

  let max = 0;
  
  // 遍历每一个关键时间点
  for (let kp of keyPoints) {
    let sum = 0;
    
    for (let i = 0; i < arr.length; i++) {
      const [s, e, c] = arr[i];

      // 如果关键时间点在任务的时间区间内，则该关键时间点所需服务器数量 += 当前任务服务器数量
      if (kp >= s && kp < e) sum += c;
    }

    max = Math.max(max, sum);
  }

  return max;
}

但是上面这个时间复杂度是O(n*m)，n就是startTime~endTime，m就是taskNum

• 1 <= taskNum <= 100000
• 0 <= startTime < endTime <= 50000

因此，差不多五十亿次循环，那肯定超时，因此我们需要对算法进行优化。

优化点1：

提前结束内层循环

比如上面例子中，关键时间点0，在和2~3时间段区间比较时，可以发现 0 < 2，因此我们其实可以在此时终止内层循环，因为内层循环是对任务的循环，而任务已经按照开始时间升序了，因此如果 0 不可能出现在2~3区间中，那么0 肯定也不会出现在后面的任务的时间区间中，比如6~9。

优化点2：

排除非必要检查区间

内层循环，每次都是从第0个任务开始，如上图，关键时间点6， 对于0~5区间和2~3区间来说，6>5，6>3，因此 关键时间点6 不可能出现在0~5区间和2~3区间中，而关键时间点数组keyPoints已经按照升序排序了，因此6后面的关键时间点必然也不可能出现在这两个区间中。

因此，我们可以定义一个ignore集合，将0~5区间和2~3区间对应的内层循环的索引 i 缓存起来，这样6后面的关键时间点，在比较前，先看看 当前内层索引 i 在不在 ignore集合中，若在则跳过。

有人肯定会有疑问，为什么不直接将内层循环的起始位置提前到 6~9 区间所在索引位置呢？

比如关键时间点6，发现前两个区间都不会和自己有交集，因此下次内层循环，就从i=3开始循环，即从6~9区间开始循环，这样关键时间点9，就可以避免再次和0~5, 2~3比较了。

我们可以看下面例子

3
2 3 1
6 9 2
0 10 1

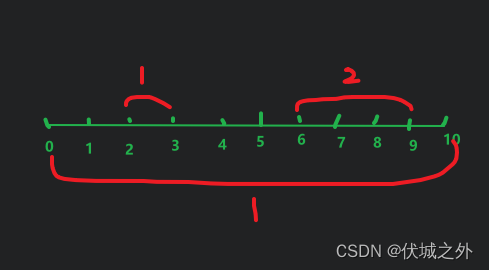
我们再看关键时间6，虽然不再2~3区间，但是还在0~10区间，因此我们不能粗暴地提前内层循环起始索引，只能用ignore集合来保存需要忽略任务对应索引 

算法源码

/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");

const rl = readline.createInterface({
  input: process.stdin,
  output: process.stdout,
});

const lines = [];
let n;
rl.on("line", (line) => {
  lines.push(line);

  if (lines.length === 1) {
    n = lines[0] - 0;
  }

  if (n && lines.length === n + 1) {
    const arr = lines.slice(1).map((line) => line.split(" ").map(Number));

    console.log(getResult(arr));

    lines.length = 0;
  }
});

function getResult(arr) {
  arr.sort((a, b) => a[0] - b[0]);

  let keyPoints = new Set();
  for (let [s, e] of arr) {
    keyPoints.add(s);
    keyPoints.add(e);
  }

  keyPoints = [...keyPoints].sort((a,b) => a-b);

  let max = 0;
  const ignore = new Set()
  
  for (let kp of keyPoints) {
    let sum = 0;
    for (let i = 0; i < arr.length; i++) {
      if(ignore.has(i)) continue// 优化

      const [s, e, c] = arr[i];

      if (kp < s) break; // 优化
      else if (kp < e) sum += c;
      else ignore.add(i)// 优化
    }

    max = Math.max(max, sum);
  }

  return max;
}