1. 进制转换

会算数值在二进制、八进制、十进制以及十六进制之间的任意转换。

会算数值的正码、反码、补码、BCD码。

2. 什么是格雷码(Gray code)，它有什么优点。

在一组二进制编码中，若任意两个相邻的数值还有1位二进制数不同，则称这种编码为格雷码，由于最大数和最小数之间也仅1位数不同，即”首尾相连”，因此又称为循环码或反射码。比如下面对于0-7数值的格雷码和二进制码关系：

十进制	二进制	格雷码
0	3'b000	3'b000
1	3'b001	3'b001
2	3'b010	3'b011
3	3'b011	3'b010
4	3'b100	3'b110
5	3'b101	3'b111
6	3'b110	3'b101
7	3'b111	3'b100

在实际电路中，两个二进制数值之间如果有多位bit不一致，在发生转换时，由于每1bit的转换时间不同，因此可能出现短暂的其它数值，在特定的情况下可能导致电路状态错误或输入错误，使用格雷码可以避免这种错误。格雷码的另一个好处是相邻数值的转换，只需要变换1bit，因此可以减少动态功耗。

3. 什么是奇偶校验位，以及它是如何算出来的？

奇偶校验位(Parity bit)是放在一个二进制数值的最后1bit，它指示1个二进制数中1的个数是偶数还是奇数。因此，有两种类型：偶校验和奇校验。如果一组给定数据位中 1 的个数是奇数，那么偶校验位就置为 1，从而使得总的 1 的个数是偶数。如果给定一组数据位中 1 的个数是偶数，那么奇校验位就置为 1，使得总的1 的个数是奇数。

奇偶校验位可以通过将二进制数据的所有bits进行XOR运算得到。它可以用于最简单的错误检测机制。

举个例子，有1个二进制数为’b1011_0011, 可以看出这个二进制数中1的个数为5个。如果采用奇校验的话，那么parity bit是0；如果使用偶校验的话，那么parity bit是1。

4. 如何使用两输入与非门(NAND gate)实现1个两输入的与门(AND gate)，1个两输入的或门(OR gate)，1个单输入的非门(NOT gate)?

我们先看与非门的逻辑表达式：Y=!(A&&B)，其中A和B是与非门的两个输入，Y是输出。

对于非门的逻辑表达式为：Y=!(A)，可以让与非门的输入A和B连接在一起，就是非门了。电路图如下：

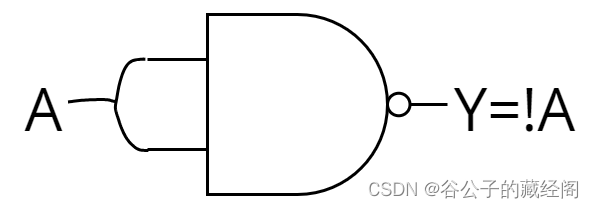
对于与门的逻辑表达式为：Y=A&&B，可以在与非门后面串上1个非门就可以了。电路图如下：

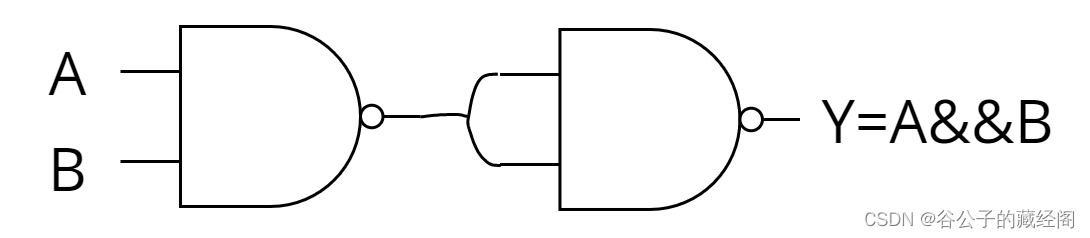
对于或门的逻辑表达式为：Y=A||B，对右边进行两次取反并用德摩根定律得到：Y=!((!A)&&(!B))，因此需要3个与非门，电路图如下：

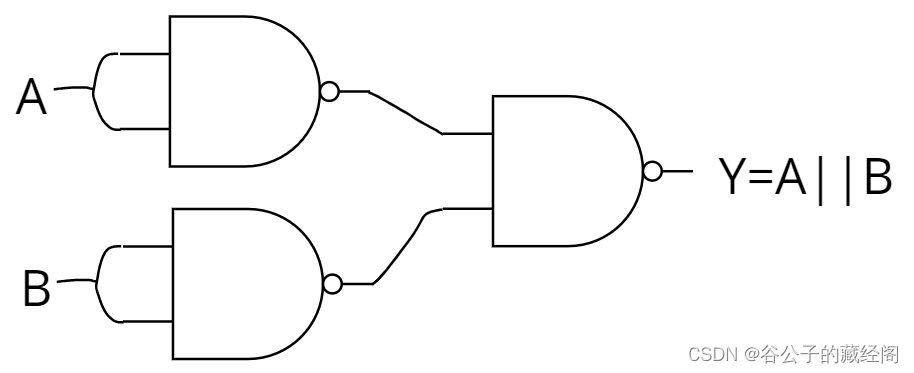
5. 如何使用两输入或非门(NOR gate)实现1个两输入的与门(AND gate)，1个两输入的或门(OR gate)，1个单输入的非门(NOT gate)?

我们先看或非门的逻辑表达式：Y=!(A||B)，其中A和B是与非门的两个输入，Y是输出。

对于非门的逻辑表达式为：Y=!(A)，可以让与非门的输入A和B连接在一起，就是非门了。电路图如下：

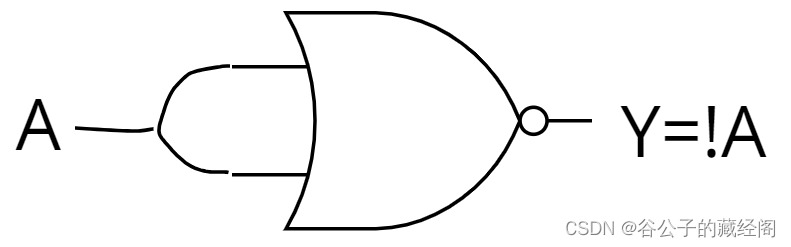
对于与门的逻辑表达式为：Y=A&&B，可以对右边进行两次取反并用德摩根定律得到：Y=!(!A || !B)，因此需要3个或非门，电路图如下：

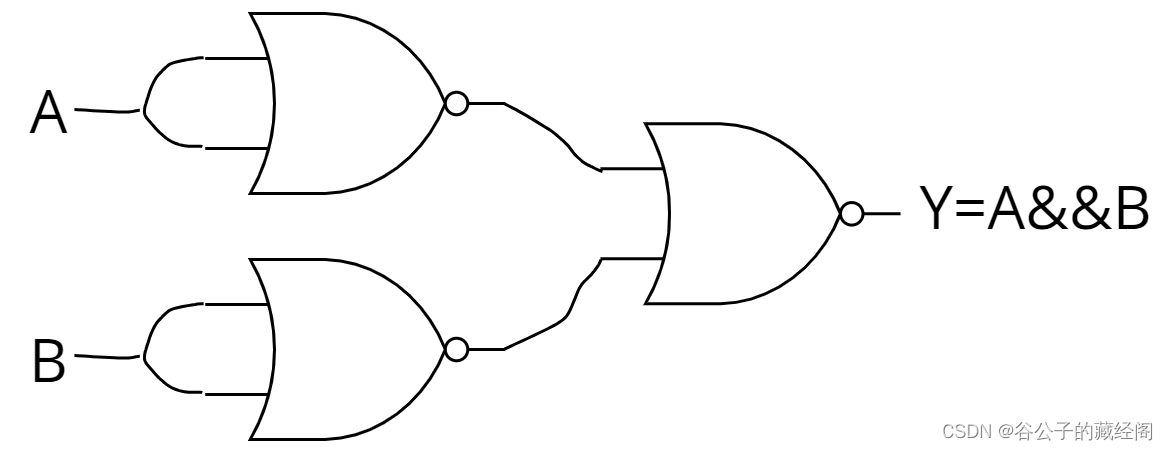
对于或门的逻辑表达式为：Y=A||B，可以在或非门后面串上1个非门就可以了。电路图如下：

6. 如何使用2选1 选择器(MUX)实现：a. 单输入非门；b. 两输入与门；c. 两输入或门；d. 两输入或非门；e. 两输入或非门；f. 两输入异或门；

这类题目的分析方法类似，我们就分析如何用2选1 MUX实现两输入与门，其余的读者可以自行分析，有问题的话可以后台留言讨论。

2选1 MUX是根据S0的值从两输入A和B中选择1个送到输出Y，它的逻辑表达式为：Y=(!S0)&&A + (S0)&&B。电路图为：

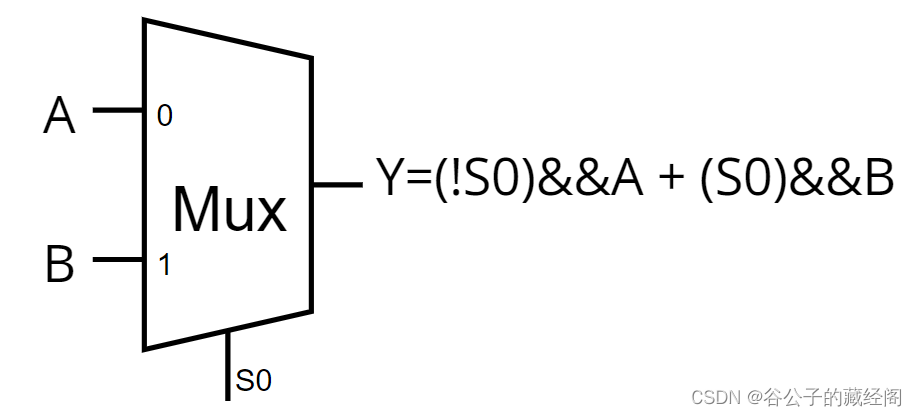
然后两输入与门的逻辑表达式为：Y=A&&B，进一步可变换为Y=!A&&A || A&&B，因此我们只要MUX的输入A和S0连接起来，就是1个与门了。电路图如下：

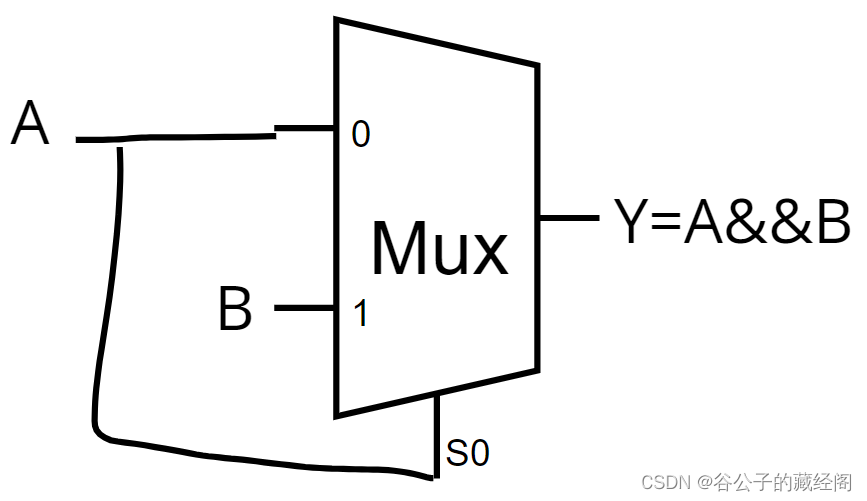
剩下的几个门的转换读者自行分析吧，思路一样，还蛮有意思的。

PS: 推荐个在线画逻辑图的网站：https://online.visual-paradigm.com/cn/diagrams/features/logic-diagram-software/