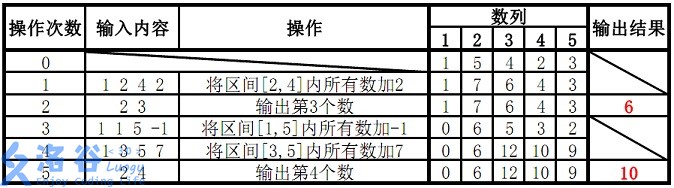
| 一、实验目的: 理解并掌握动态规划算法的基本思想和设计步骤。 | ||||||||
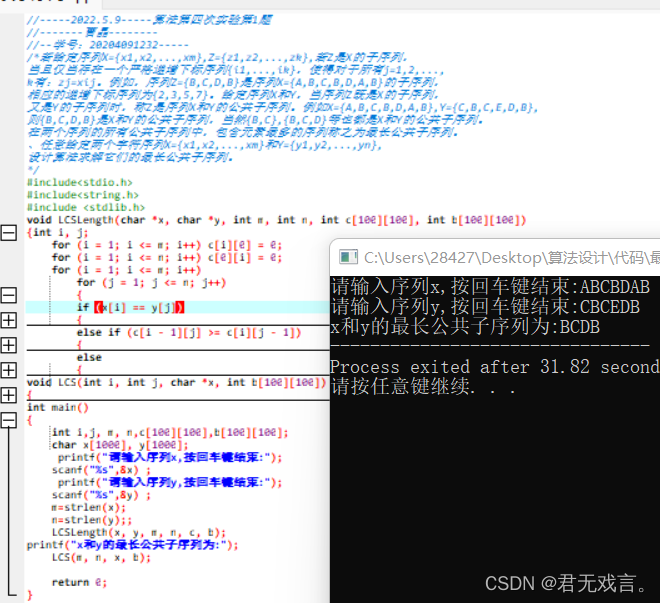
若给定序列X={x1,x2,...,xm},Z={z1,z2,...,zk},若Z是X的子序列,当且仅当存在一个严格递增下标序列{i1,...,ik},使得对于所有j=1,2,...,k有:zj=xij。例如,序列Z={B,C,D,B}是序列X={A,B,C,B,D,A,B}的子序列,相应的递增下标序列为{2,3,5,7}。 给定序列X和Y,当序列Z既是X的子序列,又是Y的子序列时,称Z是序列X和Y的公共子序列。例如X={A,B,C,B,D,A,B},Y={C,B,C,E,D,B},则{B,C,D,B}是X和Y的公共子序列,当然{B,C},{B,C,D}等也都是X和Y的公共子序列。在两个序列的所有公共子序列中,包含元素最多的序列称之为最长公共子序列。、任意给定两个字符序列X={x1,x2,...,xm}和Y={y1,y2,...,yn},设计算法求解它们的最长公共子序列。 程序代码: #include<stdio.h> #include<string.h> #include <stdlib.h> void LCSLength(char *x, char *y, int m, int n, int c[100][100], int b[100][100]) { int i, j; for(i=1;i<=m;i++)c[i][0]=0; for(i=1;i<=n;i++)c[0][i]=0; for(i=1;i<=m;i++) for(j=1;j<=n;j++) { if(x[i]==y[j]) { c[i][j]=c[i-1][j-1]+1; b[i][j]=1; } else if (c[i - 1][j] >= c[i][j - 1]) { c[i][j]=c[i-1][j]; b[i][j]=2; } else { c[i][j] = c[i][j - 1]; b[i][j] = 3; } } } void LCS(int i, int j, char *x, int b[100][100]) { if (i == 0 || j == 0) return; if (b[i][j] == 1) { LCS(i-1,j-1,x,b); printf("%c", x[i]); } else if (b[i][j] == 2) LCS(i-1,j,x,b); Else LCS(i,j-1,x,b); } int main() { int i,j, m, n,c[100][100],b[100][100]; char x[1000], y[1000]; printf("请输入序列x,按回车键结束:"); scanf("%s",&x) ; printf("请输入序列y,按回车键结束:"); scanf("%s",&y) ; m=strlen(x); n=strlen(y); LCSLength(x, y, m, n, c, b); printf("x和y的最长公共子序列为:"); LCS(m, n, x, b); return 0; } 程序测试及运行结果:
| ||||||||
| 分析与讨论:
我的思路是,本题采用动态规划法,最重要的就是找出递推公式,也是本体解开的核心,求出递推公式,再自下而上的求解最优值。设序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}的最长公共子序列为Z={z1,z2,…,zk} ,则:若xm=yn,则zk=xm=yn,且zk-1是xm-1和yn-1的最长公共子序列。若xm≠yn且zk≠xm,则Z是xm-1和Y的最长公共子序列。若xm≠yn且zk≠yn,则Z是X和yn-1的最长公共子序列。 那么最长公共子序列的长度可以表示为:
在编写程序的时候,当两个序列其中一个为零的时候,那么公共子序列长度肯定为零所以由c[i][0]=0和c[0][j]=0,然后根据最长公共子序列长度,用if与语句分三种情况讨论,并对c[i][j]进行赋值。
求解最长公共子序列的特点:两个序列的最长公共子序列不是唯一的,其子序列不能改变其元素的先后顺序。 动态规划法的优点:能够得到全局最解。 动态规划法缺点:数值方法求解时存在维数灾并且没有统一的标准模型。 |
算法程序设计 之 最长公共子序列(4/8)
news2026/2/11 2:25:20
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/672253.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
智能家居APP软件开发有何优势?
传统家居行业营销模式已经无法满足现代人多样化个性化的需求,也跟不上互联网时代的发展步伐了,很多传统家居行业都陷入了营销困境。通过智能家居APP软件开发,可以利用互联网改造传统模式,探索新的发展模式,可以说智能家…
Bootstrap 简介
文章目录 Bootstrap 简介什么是 Bootstrap?Bootstrap 包的内容Bootstrap 实例 Bootstrap 简介 什么是 Bootstrap?
Bootstrap 是一个用于快速开发 Web 应用程序和网站的前端框架。Bootstrap 是基于 HTML、CSS、JAVASCRIPT 的。 历史
Bootstrap 是由 Twi…
【软件测试知识】什么是持续集成?
持续集成是一种 DevOps 软件开发实践。采用持续集成时,开发人员会定期将代码变更合并到一个中央存储库中,之后系统会自动运行构建和测试操作。持续集成通常是指软件发布流程的构建或集成阶段,需要用到自动化组件(例如 CI 或构建服…
EasyUI表格增加筛选和导出的方法
一、前言
最近写前端页面,要从后台查询表格数据;
查到数据后,就想增加个数据筛选功能,如果再查后台的话会影响效率(还得加参数、再调用后台接口、后台再执行sql),就想前端能不能自己筛选下已经…
车载以太网 - 传输层 - TCP通信过程
目录
TCP 通信阶段
1、连接建立Connection establishment
2、数据传输 Data transfer
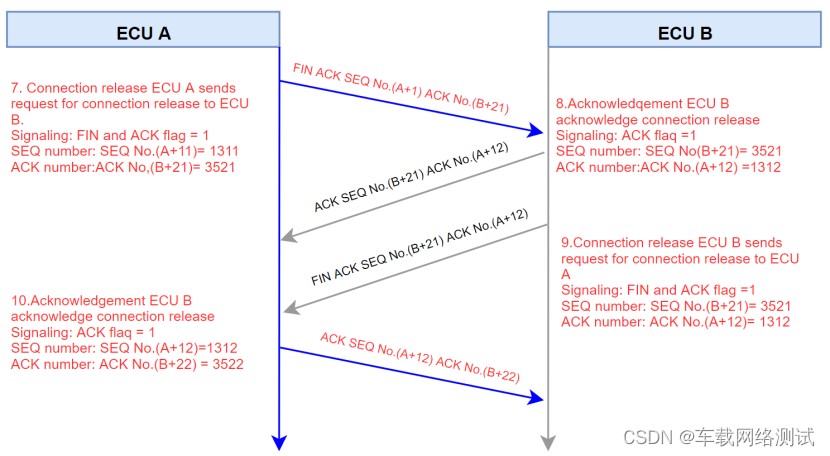
3、连接释放 Connection release
TCP通信的三个阶段:
TCP连接(三次握手)
1、Client(ECUA) -> Server(ECU B)第一次握手
2、Server -> Client 第二次握手…
软件工程基础速通教程(北京理工大学)
文章目录 前言软工上课情况考后感题型分析概念部分大题部分数据流图和数据字典数据流图数据字典 结构化设计工具程序流程图盒图(N-S图)PAD图判定表和判定树PDL(伪码) 软件测试白盒测试法语句覆盖判定覆盖,条件覆盖&…
【MMDetection3.0】训练自己的数据集
本文记录下MMDetection3.0版本,即截至目前最新的版本,训练自定义数据集的过程。当前MMDetection已经封装的很好了,虽然易于使用,但其API也愈发复杂,对于新手不太友好,这里记录下自己的踩坑经历。
数据部分…
音视频开发:Qt在视频剪辑3D桌面软件获胜, 嵌入式不敌安卓
1 Qt Android嵌入式应用层开发方向对比
大家都知道啊,做嵌入式linux设备,一些没有屏幕,比如安防摄像头,门铃之类的,另外一些嵌入式设备是有触控屏,在触控屏上还跑应用软件的,这种比如商场各种…
citywalk话题增长704.76%,小红书本地化内容营销怎么玩?
2023年初发布的《2023小红书年度生活趋势:投入真实生活》报告中提到,今后年轻人会更加意识到周围和附近的重要性,在十大生活趋势预测中,近邻升温(2022年相关笔记数量同比上涨213%)、野到家门口(…
建立小型医学数据库(总结)
建立小型医学数据库 小型医学数据库可以用于存储和管理医学数据,如患者病历、药品信息、试验结果等。这对于医疗机构和科研机构来说非常必要,可以提高数据管理和共享的效率,进而促进医学研究和诊疗水平的提升。
建立小型医学数据库有以下基本…
转发和重定向的区别及其原理
在web应用中完成资源的跳转
在一个web应用中完成资源的跳转可以通过转发或者重定向两种方式, 跳转的资源只要是服务器内部合法的资源即可(如Servlet、JSP、HTML…)
转发机制使用场景: 某个Servlet向request域当中绑定了数据,希望从其他Servlet当中把request域里面…
【Python】Django 基础知识
系列文章目录 提示:阅读本章之前,请先阅读目录 文章目录 系列文章目录前言安装启动项目查看所有子命令主要文件setting 配置项URL 请求路径path 转换器HttpResponse 输出中文乱码models的objects代码自动补全views的request 代码自动补全views的request.…
沃尔玛、亚马逊跨境电商如何实现自养账号采退、海淘及测评的
今天曹哥还是针对下亚马逊、沃尔玛跨境平台如何实现自己养买家号可以给自己采购、海淘及测评等技术问题
首先你要有一个稳定的环境方案,这个是做自养号采购、海淘及测评的基础。环境有很多,从早期的虚拟机,模拟机,云手机…
[进阶]Java:IO流分类、文件字节输入流、读取字节数据、避免乱码问题
IO流概述
I表示intput,是数据从硬盘文件读入到内存的过程,称之输入,负责读。O表示output,是内存程序的数据从内存到写出到硬盘文件的过程,称之输出,负责写。 IO流的分类
按流的方向分 按流中的数据最小单…
树状数组(入门附模板)
声明:本篇文章图片非原创 目录
简介
lowbit函数
结构分析
单点修改,区间查询
区间修改,单点查询
区间修改,区间查询
模板题
树状数组1–单点修改,区间查询
题目描述
输入格式
输出格式
输入输出样例
输入 #1
输出 #1
说明/提示
分析
代码
树状数…
移动机器人路径优化:基于Q-learning算法的移动机器人路径优化(提供MATLAB代码)
一、Q-learning算法
Q-learning算法是强化学习算法中的一种,该算法主要包含:Agent、状态、动作、环境、回报和惩罚。Q-learning算法通过机器人与环境不断地交换信息,来实现自我学习。Q-learning算法中的Q表是机器人与环境交互后的结果&#…
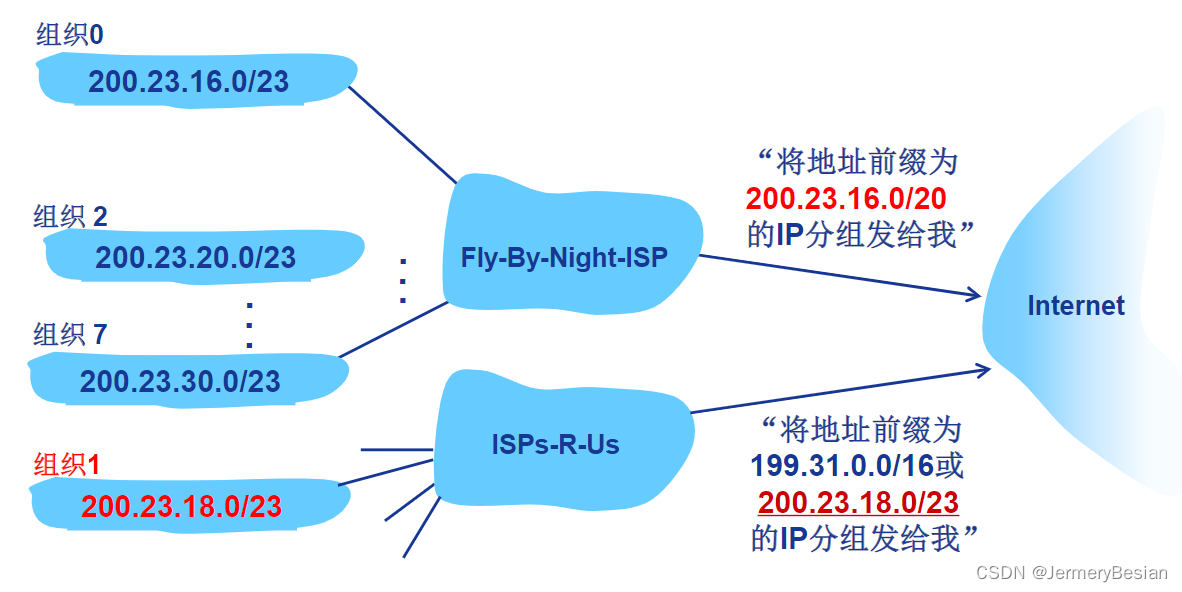
哈工大计算机网络课程网络层协议详解之:CIDR与路由聚集
哈工大计算机网络课程网络层协议详解之:CIDR与路由聚集 文章目录 哈工大计算机网络课程网络层协议详解之:CIDR与路由聚集CIDR与路由聚集CIDR路由聚集 CIDR与路由聚集
CIDR
CIDR:无类域间路由(CIDR:Classless InterDo…
2.4C++派生类的函数
C 派生类的构造函数
在C中派生类的构造函数,必须调用基类的构造函数,来初始化从基类继承的数据成员。
具体有两种形式:
1、默认构造函数 2、带参数的构造函数 上面的我写的代码中,DerivedClass 构造函数的初始化列表中调用了 …
前缀和以及map混用,打开思路
补一个坑
目录
以力扣560为例:
力扣1248,优美子数组 力扣974 和可被 K 整除的子数组
力扣523.连续的子数组和 浅谈一下前缀和: 我们通过前缀和数组保存前 n 位的和,presum[1]保存的就是 nums 数组中前 1 位的和,也…
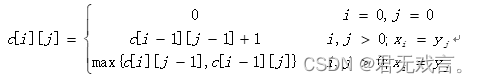






![[进阶]Java:IO流分类、文件字节输入流、读取字节数据、避免乱码问题](https://img-blog.csdnimg.cn/52d67dddf9e64b9696c2e7fc58668005.png)