叮叮咚咚,新一期来袭,我还在吃桃子,吃桃子,吃桃子。。。串和python的字符串差不多,数组和广义表像是python的list
文章目录
- 串(string) - 字符串
- 概念及术语
- 串的类型定义
- 存储结构(同线性表)
- 串的模式匹配算法
- BF 算法
- KMP算 法 (特点:速度快 )
- 数组
- 数组的定义
- 一维数组
- 二维数组
- 数组特点
- n维数组的数据类型定义
- 数组的顺序存储
- 特殊矩阵的压缩存储
- 对称矩阵
- 三角矩阵
- 对角矩阵
- 稀疏矩阵
- 广义表
- 概念
- 性质
- 广义表和线性表的区别?
- 基本运算
- 案例分析
- TO BE CONTINUED...
串(string) - 字符串
概念及术语
-
定义: 零个或多个任意字符组成的有限序列,是一种内容受限的线性表

-
子串 : 串中任意个连续字符组成的子序列称为该串的子串, 空串和串本身都是子串,不含本身的是真子串。
-
主串 : 包含子串的串相应地称为主串。
-
字符位置 : 字符在序列中的序号为该字符在串中的位置 。
-
子串位置 : 子串第一个字符在主串中的位置 。
-
空格串 : 由一个或多个空格组成的串 , 与空串不同。
-
串相等 : 当且仅当两个串的长度相等并且各个对应 位置上的字符都相同时 , 这两个串才是相等的 。
-
所有的空串是相等的。
串的类型定义


存储结构(同线性表)
-
顺序串(顺序存储结构)(更常用因不经常插入删除)
#define MAXLEN 255 typedef struct{ char ch[MAXLEN+1]; // 存储串的一维数组,实际范围0-255(0可能保留不用) int length; // 串的当前长度长度 }SString; -
链串(链式存储结构)

// 块链结构 #define CHUNKSIZE 80 // 块的大小可有客户定义 typedef struct Chunk{ char ch[CHUNKSIZE]; struct Chunk *next; }Chunk; typedef struct LString{ Chunk *head,*tail; // 串的头指针和尾指针 int curlen; //串的当前长度 }LString; //字符串的块链结构
串的模式匹配算法
确定主串中所含子串(模式串)第一次出现的位置(BF&KMP)
BF 算法
- (Brute-Force, 又称古典的 、 经典的 、 朴素的 、 穷举的 )
思路:从主串的每一个字符开始依次与模式串字符进行比较
Index(S,T,pos)
-
将主串的第 pos 个字符和模式串的第一个字符比较 ,若相等,继续逐个比较后续字符;
-
若不等,从主串的下一字符起(回溯) , 重新与模式串的第一个字符比较
-
直到主串的一个连续子串字符序列与模式串相等。 返回值
为 S 中与 T 匹配的子序列第一个字符的序号 , 即匹配成功 。
否则 , 匹配失败 , 返回值 0
int Index_BF(SString S, SString T, int pos){ int i=pos; j=1; // 主串i的位置从1开始pos>=1 while(i<=S.length&&j<=T.length){ if (S.ch[i]==T.ch[j]) {++i; ++j;} // 主串和子串依次匹配下一个字符 else {i=i-j+2; j=1} // 字符不相等,主串i回溯位置到(i-(j-1)+1),j回到1 } if (j>T.length) return i-T.length; // 返回模式串匹配成功后主串对应首字符的下标 else return 0; } -
时间复杂度为
(n-m)*m+m --> (n-m+1)*m--> O(n*m)(当m<<n)
KMP算 法 (特点:速度快 )
利用已经部分匹配的结果而加快模式串的滑动速度 ?
且主串 S 的指针 i 不必回溯 ! 可提速到 O( n+m )

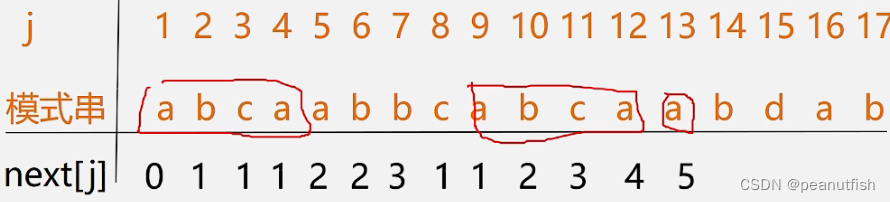
j的位置可以根据模式串来确定 ,定义next[j]函数 , 表明当模式中剃个字符与主串中相应字符 " 失配 " 时 , 在模式中需重新和主串中该字符进行比较的字符的位置 。

int Index_KMP(SString S, SString T, int pos){
int i=pos; j=1; // 主串i的位置从1开始pos>=1
while(i<=S.length&&j<=T.length){
if (S.ch[i]==T.ch[j]) {++i; ++j;} // 主串和子串依次匹配下一个字符
else j=next[j] // 通过next[j]得到j的位置,i不用回溯
}
if (j>T.length) return i-T.length; // 返回模式串匹配成功后主串对应首字符的下标
else return 0;
}
void get_next(SString T, int &next[]){
i=1; next[1]=0; j=0;
while (i < T.length){
if (j==0 || T.ch[i]==T.ch[j]){
++i; ++j;
next[i]=j;
}
else j=next[j];
}
}
next[j]的改进- nextval[j]
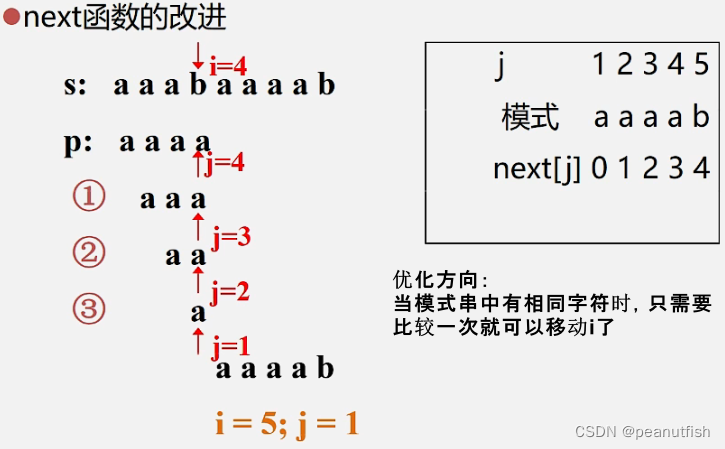

void get_nextval(SString T, int &nextval[]){
i=1; nextval[1]=0; j=0;
while (i < T.length){
if (j==0 || T.ch[i]==T.ch[j]){
++i; ++j;
if (T.ch[i]==T.ch[j]) nextval[i]=j;
else nextval[i]=nextval[j];
}
else j=nextval[j];
}
}
数组
数组的定义
按一定格式排列起来的具有相同类型的数据元素的集合
一维数组
若线性表中的数据元素为非结构的简单元素,则称为一维数组 。
其逻辑结构有线性结构,定长的线性表 。
声明格式 : 数据类型 变量名称 [长度]
二维数组

声明格式: 数据类型变量名称 [行数] [列数] ,eg: int num[5][8]
在 C 语言中 ,一个二维数组类型也可以定义为一维数组类型
( 其分量类型为一维数组类型 ),
即 :typedef elemtype array2[m][n];
等价于 :
typedef elemtype array1[n];
typedef array1 array2[m];
三维数组 : 若二维数组中的元素又是一个一维数组 , 则称作三维数组 。。。。
n维数组:若n-1维数组中的元素又是一个一维数组结构则称为n维数组 。
线性表是数组结构的一个特例,数组结构又是线性表结构的扩展。
数组特点
结构固定(定以后维数和维界不再改变),基本操作就是初始化,销毁,取元素,修改元素 。
n维数组的数据类型定义


数组的顺序存储
一维数组存储位置

二维数组存储
-
以行优先 - JAVA, C, BASIC ,COBOL ,PASCAL

-
以列优先 - FORTRAN

三维数组 按页行列存放,页优先的顺序存储
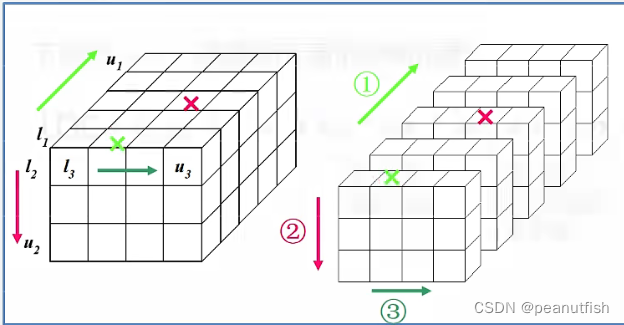

扩展到n维数组存储位置计算


特殊矩阵的压缩存储
-
压缩存储定义:若多个数据元素的值都相同 , 则只分配一个元素值的存储空间 , 且
零元素不占存储空间 。 -
特殊矩阵:对称矩阵,对角矩阵,三角矩阵,稀疏矩阵(非零元素个数一般<5%)
对称矩阵

只需存储一半元素,存储个数为每一行个数相加,即1+2+3+…+n=n(n+1)/2
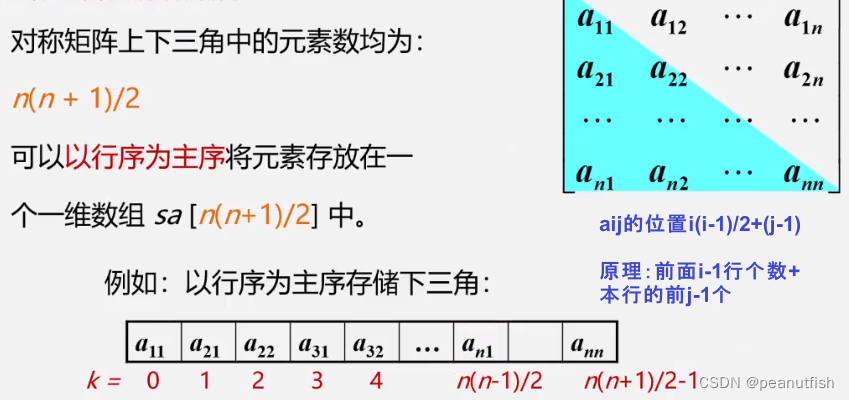
任一个元素存在一维数组的位置aij的位置i(i-1)/2+(j-1) 原理:前面(i-1)行个数+本行的前(j-1)个元素
三角矩阵

对角矩阵
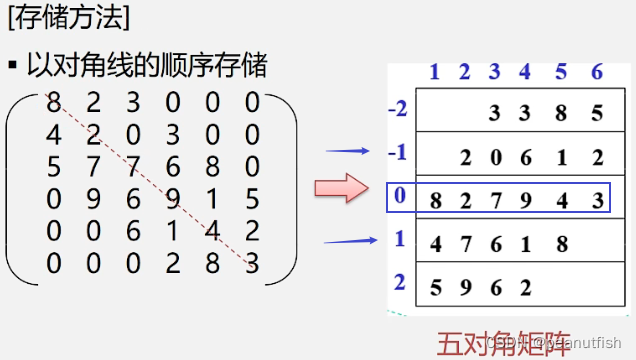
[ 特点 ] 在n×n的方阵中,所有非零元素都集中在以主对角线为中心的带状区域中,区域外的值全为0 ,则称为对角矩阵 。 常见的有三对角矩阵 、 五对角矩阵 、 七对角矩阵等 。(3/5/7条数据)

稀疏矩阵
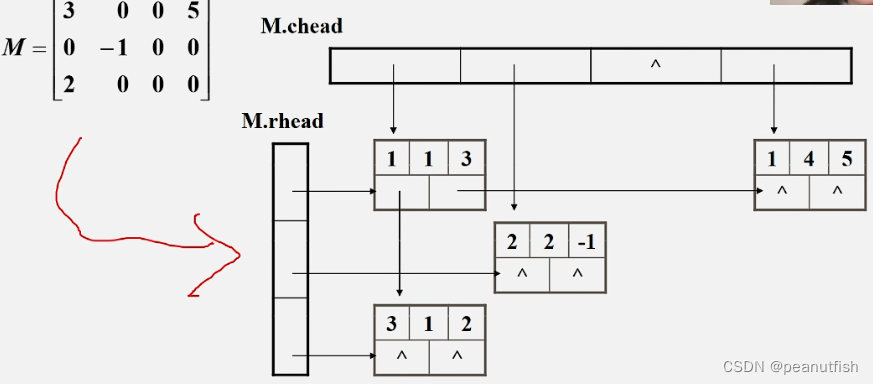
三元组(行,列,值) 和矩阵维数(总行,总列)来唯一确定一个元素的位置

-
三元组顺序表又称有序的双下标法。
-
优点:非零元素在表中按行序有序存储
-
缺点:不能随机存储,按行号存取某一行中的非零元素要从头开始查找
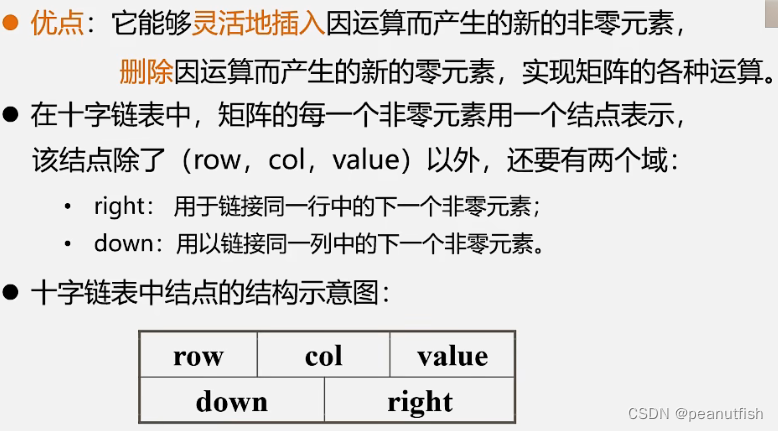
十字链表 法存储稀疏矩阵
广义表
概念
广义表( 又称列表 Lists) 是 n>=0 个元素 a0, a1, a2…an-1的有限序列 , 其中每一个或者是原子 , 或者是一个广义表 。

性质


广义表和线性表的区别?
- 广义表是线性表的推广,线性表是广义表的特例
- 广义表的结构相当灵活 , 在某种前提下 , 它可以兼容线性表 、 数组 、
树和有向图等各种常用的数据结构 。
基本运算
GetHead(L): 求非空广义表的第一个元素,可以是一个原子或者一个子表
GetTail(L):非空广义表去掉表头元素以外其他元素所构成的表。
案例分析
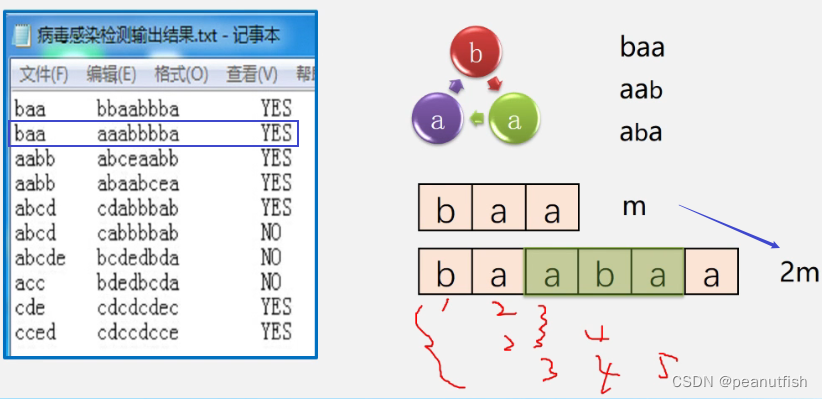
病毒感染检测(病毒RNA是环状)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-tK0IY99o-1687358835821)(../resources/image-20230621224425435.png)]](https://img-blog.csdnimg.cn/b1091249707845e399005553c4372d80.png)