Part.I Introduction

在平时阅读文献或者整理笔记时，经常会看到各种各样的有关误差方程的表述。因为不同学者习惯不同，所以可能会造成一定的困扰。阅读的时候还好，写作的时候往往会因为过于苛求正确性而自己把自己搞晕。为了防止下一次蒙圈，就花点时间好好梳理一下思路。希望这篇博文能尽量地把握误差方程的『本质』。

此乃笔者的个人理解，仅供参考。由于笔者水平有限，不当之处还望不吝赐教。

Part.II 误差方程的探讨

Chap.I 符号表示

下面是常用的记号

• $L$：观测值
• $X$：待估参数
• $X^0$：待估参数估值
• $B$：设计矩阵
• $\Delta$：观测噪声，真误差
• $x$：待估参数改正数 $X-X^0$
• $l$：观测值与泰勒展开 0 阶项之差 $L-f(X^0)$
• $v$：观测值的改正数，用于补偿观测误差 $\Delta$
• $P$：权阵

Chap.II 误差方程的含义

下面从原始观测方程出发，对误差方程的表达式进行推导。
设观测值 $L$ 和待估参数 $X$ 具有如下关系：

$$L=f(X)$$
首先假设待估参数初值为 $X^0$，基于此对函数进行线性化，忽略二次以上项，并考虑到观测噪声 $\Delta$，于是有

$$L=f(X^0)+B(X-X^0)+\Delta$$
实际上，这里的 $\Delta$ 不仅包含了观测噪声，还包含了泰勒展开忽略二次及以上项引入的误差。记 $l=L-f(X^0)$，待估参数改正数为 $x=X-X^0$，并引入观测值的改正数 $v$ 用于补偿真误差 $\Delta$（即 $v=-\Delta$），于是
$$-\Delta =B(X-X^0)-(L-f(X^0))$$
便可写为：
$$v=Bx-l$$
此乃大名鼎鼎的误差方程。

Chap.III 误差方程的其他形式

注意：根据上面的误差方程，我们基于最小二乘准则求得的解

$$v=(B^{T}PB{)}^{-1}{B}^{T}Pl$$
并不是待估参数，而是待估参数的改正数。也就是说，我们直接求的并不是待估参数，而是待估参数的改正数。

---

另外，基于式

$$(L-f(X^0))-\Delta =B(X-X^0)$$
一般假设 $\Delta$ 服从正态分布，也就是说它的期望为 0，于是误差方程还可以写为下面的形式。
$$E(l)=Bx$$
其中 $E(\cdot )$ 表示求期望算子，这种形式，笔者觉得比较简洁，也是目前笔者比较倾向使用的形式。

---

因为我们的目的是求待估参数 $X$，并不是待估参数的改正数 $x$，若用 $x$ 表示的话，叙述起来不免有些麻烦；并且 $X=X^0+x$，$X$ 与 $x$ 只是相差了一个常数 $X^0$。所以，就出现了下面这种误差方程的表示形式：
$$E(l)=BX$$
$$v=BX-l$$
注意，这两种表示形式理论上并不严格，只是出于书写方便，遇到了，要明白式中的 $X$ 实际上指的是 $x$。

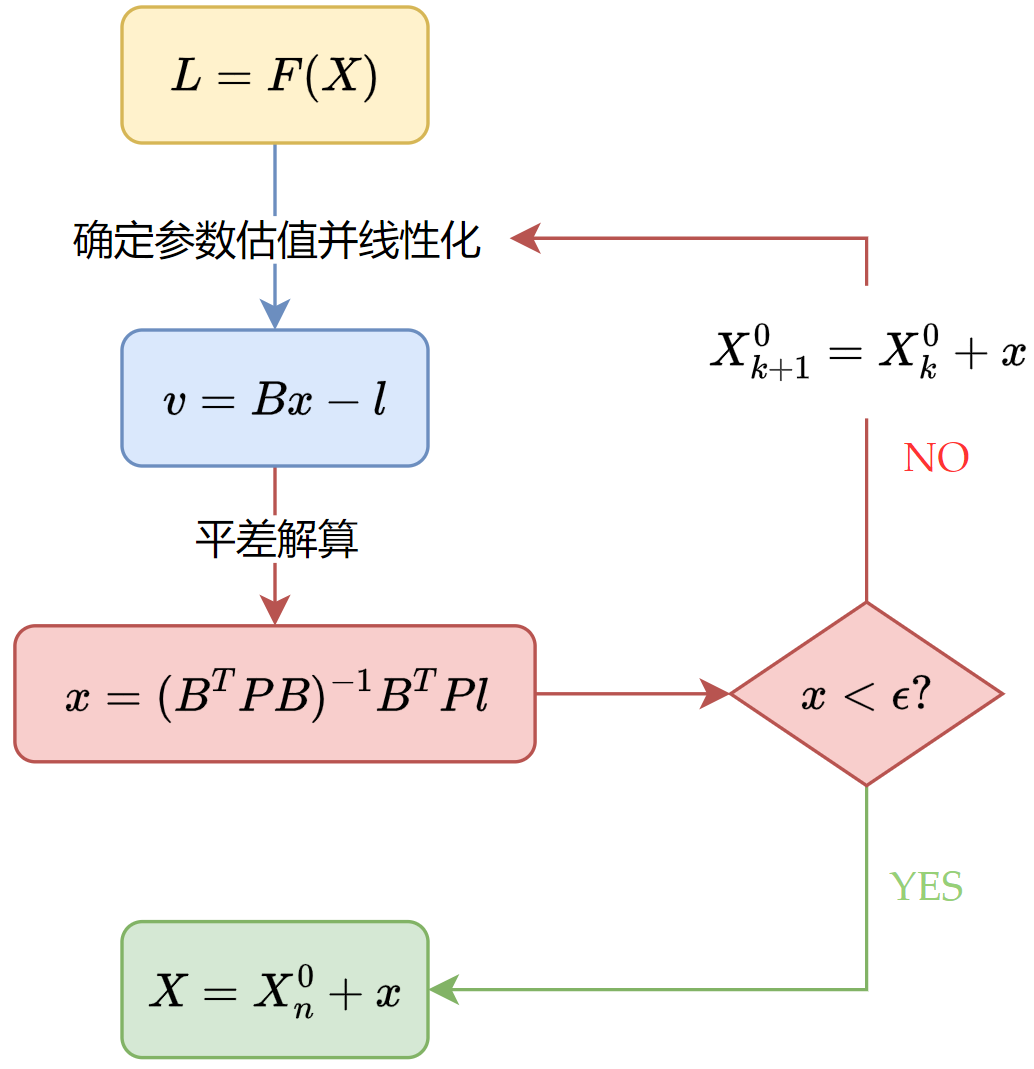
Chap.IV 平差的大致流程

笔者印象当中的平差是下面的流程，关于得到 $x$ 后更不更新 $B$ 矩阵，这是一个值得思考的问题。

Part.III 误差方程的表示形式

基于上，下面对误差方程的表示形式进行一个汇总整理
$$v=Bx-l$$
$$E(l)=Bx$$
$$E(l)=BX$$

$$v=BX-l$$
上面两个是理论上的表述方式，下面两个是出于方便描述而作的微调。