✨博文作者:烟雨孤舟
💖 喜欢的可以 点赞 收藏 关注哦~~✍️ 作者简介: 一个热爱大数据的学习者
✍️ 笔记简介:作为大数据爱好者,以下是个人总结的学习笔记,如有错误,请多多指教!
目录
数据结构的概念
抽象数据类型的表示与实现
算法和算法分析
常见的数据结构
常见的算法
数据结构的概念
数据结构(英语:data structure)是计算机中存储、组织数据的方式。
数据结构是一种具有一定逻辑关系,在计算机中应用某种存储结构,并且封装了相应操作的数据元素集合。它包含三方面的内容,逻辑关系、存储关系及操作。
数据结构的概念:数据结构是一门研究非数值计算的程序设计问题中计算机的操作对象以及他们之间的关系和操作的学科。
数据结构的描述:ADT和C语言
数据结构的内涵:数据对象及其内部数据元素的关系描述了数据结构的静态特征。
增删改查等基本操作(算法)描述了数据结构的动态特征。
数据结构=数据(数据对象)+结构(数据元素之间的关系)
数据:信息的载体
数据元素:数据的基本单位
数据项:具有独立含义的最小标识单位;数据元素由数据项构成。
数据对象:具有相同性质的数据元素的集合。
在数据结构里数据就是指的数据对象。
案例:
数据元素:运动员
数据项:运动员的姓名 出生日期 身高 性别 俱乐部名称
数据对象:某俱乐部的所有运动员
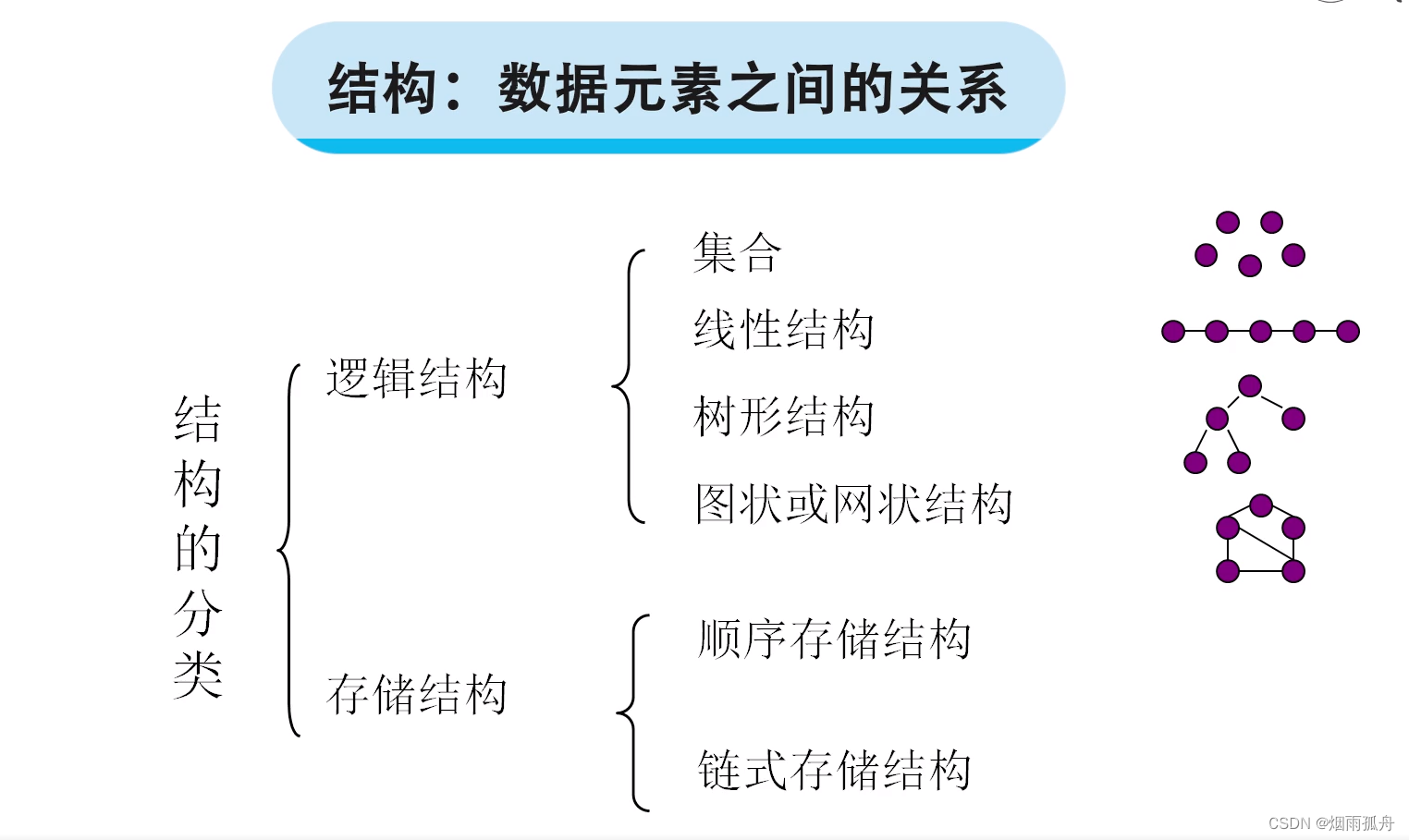
结构:数据元素之间的关系
结构的分类:逻辑结构、存储结构
逻辑结构:集合、线性结构、树形结构、网状或网状结构
存储结构:顺序存储结构、链式存储结构
集合:集合之间的元素是不存在任何关系的,他们只属于某个集合
线性结构:线性结构的元素是一对一的关系
树形结构:树形结构是一对多的关系
网状或网状结构:网状或网状结构是多对多的关系
在计算机中算法的设计主要取决于逻辑结构,算法的实现取决于存储结构
顺序存储结构;数据元素存放在一组地址连续的存储单元中,逻辑上相邻的元素在存储器中仍然相邻
链式存储结构:数据元素可以放在不连续的存储单元中,数据元素之间的关系通过指针确定,逻辑上相邻的元素在存储器上不一定是相邻的

抽象数据类型的表示与实现
数据结构的表示和实现:可用抽象数据类型定义数据结构及其操作。
抽象数据类型可用三元组(D,S,P)表示
D:数据对象及ADT
S:D上的关系集(Status)
P:对D的基本操作集
ADT 抽象数据类型名{
数据对象:<数据对象的定义>
数据关系:<数据关系的定义>
基本操作:<基本操作的定义>
}ADT抽象数据类型名
基本操作定义格式:
基本操作名(参数表)
初始条件:(初始条件描述)
操作结果:(操作结构描述)
1.常量和类型的预定义:
使用关键字define
#define TRUE 1
typedef int Status;
2.数据元素类型约定为ElemType,由用户定义,在数据结果结构中我们经常把它定义为整型或字符型
3.基本操作都是用函数描述的。在形参表中,以&开头的参数是引用参数。
形参表里有两种参数,一种是引用参数,一种是值参数
4.一些类C语言的语句是不能直接编译运行的:去成组赋值A=[0..9]=B[0..9];
算法和算法分析
算法是对数据局结构里面基本操作的描述
算法:是对特定问题求解步骤的一种描述,是指令的有限序列。
算法的5个特性:有穷性、确定性、可行性、输入、输出
有穷性指的是算法可以在有穷的步骤和有穷的时间被完成
确定性指的是语句没有歧义
可行性是指操作可以通过基本的一些操作来实现
输入输出是指算法可以有0个或多个输入和1个或多个输出
算法设计的要求:正确性、可读性、健壮性、效率和低存储量的要求
算法分析:可以通过算法效率度量来描述,第一是时间复杂度,第二是空间复杂度
算法效率的度量:时间复杂度(time complexity)
算法的存储空间需求:空间复杂度(space complexity)
时间复杂度:一般情况下,算法中基本操作的重复次数是问题规模n的某个函数F(n),算法的时间复杂度记作T(n)=O(f(n))
O是Order表示数量级,也就是说表示f(n)和T(n)是具有相同数量级的函数
空间复杂度:类似空间复杂度的定义,设问题的规模为n,算法的空间复杂度记作S(n)=O(f(n))
O是Order表示数量级,随着问题规模n的增大,算法运行所需要的存储量的增长率与f(n)的增长率相同。
在问题中如果输入数据所占空间只取决于问题本身和算法无法则只需要分析除输入和程序之外的额外空间
#时间复杂度案例
sum =0
for(i=1;i<=n;i++)
for(j=1;j<=i;j++)
sum =sum+1;
//分析
函数具有两个for循环,案例是一个嵌套的for循环
外层的for循环是由i等于1变化到n,内层的for循环是由j等于1变化到n
i=1时,内层循环是循环一次
i=2时,内层循环是循环两次
......
i=n时,内层循环是循环n次
所以第四行代码执行次数为:f(n)=1=2+3+...+n=n(n+1)/2=n^2+0.5n
时间复杂度:T(n)=O(f(n))=O(n^2+0.5n)=O(n^2)
时间复杂度我们只取变化频率最高的项,即n方,所以最终时间复杂度是0n方
#空间复杂度案例:交换a和b的值
t=a;a=b;b=t;
程序段只需要1个辅助空间存储变量t。空间复杂度S(n)=O(1)常见的数据结构
栈(Stack):栈是一种特殊的线性表,它只能在一个表的一个固定端进行数据结点的插入和删除操作。
队列(Queue):队列和栈类似,也是一种特殊的线性表。和栈不同的是,队列只允许在表的一端进行插入操作,而在另一端进行删除操作。
数组(Array):数组是一种聚合数据类型,它是将具有相同类型的若干变量有序地组织在一起的集合。
链表(Linked List):链表是一种数据元素按照链式存储结构进行存储的数据结构,这种存储结构具有在物理上存在非连续的特点。
树(Tree):树是典型的非线性结构,它是包括,2 个结点的有穷集合 K。
图(Graph):图是另一种非线性数据结构。在图结构中,数据结点一般称为顶点,而边是顶点的有序偶对。
堆(Heap):堆是一种特殊的树形数据结构,一般讨论的堆都是二叉堆。
散列表(Hash table):散列表源自于散列函数(Hash function),其思想是如果在结构中存在关键字和T相等的记录,那么必定在F(T)的存储位置可以找到该记录,这样就可以不用进行比较操作而直接取得所查记录。
常见的算法
数据结构研究的内容:就是如何按一定的逻辑结构,把数据组织起来,并选择适当的存储表示方法把逻辑结构组织好的数据存储到计算机的存储器里。算法研究的目的是为了更有效的处理数据,提高数据运算效率。数据的运算是定义在数据的逻辑结构上,但运算的具体实现要在存储结构上进行。一般有以下几种常用运算:
检索:检索就是在数据结构里查找满足一定条件的节点。一般是给定一个某字段的值,找具有该字段值的节点。 插入:往数据结构中增加新的节点。 删除:把指定的结点从数据结构中去掉。 更新:改变指定节点的一个或多个字段的值。 排序:把节点按某种指定的顺序重新排列。例如递增或递减。