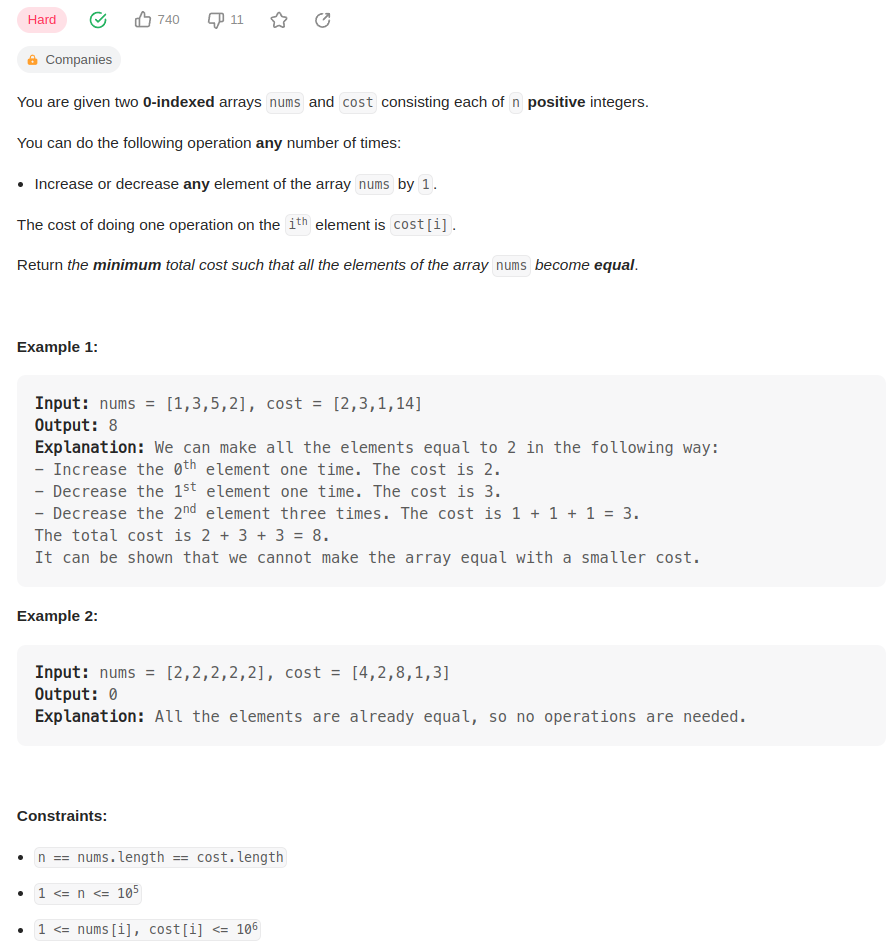
数组nums的元素每次可进行下面的操作：
每个元素+1 或者 -1。
操作一次的cost是cost[i].
问把nums的元素全部变为相等的元素需要的最小的cost.

思路：

nums的元素全部变为相等的元素，这个相等的元素是多少，现在不知道。
一旦知道了目标元素是多少，就可以直接计算cost.

所以需要求解的其实是这个相等的目标元素是多少。
它的可能性是 1 ~ 10⁶ （nums[i]的范围），要在这个范围内找到一个数字，使cost最小。
那么需要用到binary search.

存在一个数字，nums所有元素在+1，-1的操作下变为这个数字的cost最小，
假设数字是a, 那么cost(a-1) > cost(a), cost(a+1) > cost(a),
在binary search中，如果cost(mid-1) > cost(mid), cost(mid+1) > cost(mid),
那么mid就是要找的目标数字。

如果cost(mid) > cost(mid-1), 说明要向左边去找，right=mid-1, 反之left = mid+1.

class Solution {
    public long minCost(int[] nums, int[] cost) {
        int left = 1;
        int right = 1000000;

        long res = Long.MAX_VALUE;

        //binary search
        while(left <= right) {
            int mid = left + (right-left)/2;
            long curCost = findCost(nums, cost, mid);
            res = Math.min(res, curCost);
            long rCost = findCost(nums, cost, mid+1);
            long lCost = findCost(nums, cost, mid-1);

            if(curCost < lCost && curCost < rCost) return res;
            else if(curCost > rCost) left = mid+1;
            else right = mid-1;
        }
        return res;
    }

    long findCost(int[] nums, int[] cost, int value){
        long res = 0;
        for(int i = 0; i < nums.length; i++) {
            long diff = Math.abs(nums[i] - value);
            res += diff * cost[i];
        }
        return res;
    }
}

或者直接先找目标数字，再求cost.
这个方法更快一些。
但是很神奇的是如果把mid=(left+right+1)/2换成mid=left+(right-left)/2就会TLE。

class Solution {
    public long minCost(int[] nums, int[] cost) {
        int left = 1;
        int right = 1000000;

        while(left < right){
            //mid = left+(right-left)/2会TLE
            int mid = (left + right +1)/2;
            long curCost = findCost(nums, cost, mid);
            long lCost = findCost(nums, cost, mid-1);

            if(curCost >= lCost) right = mid - 1;
            else left = mid;
        }
        return findCost(nums, cost, left);
    }

    long findCost(int[] nums, int[] cost, int val)
    {
        long ans = 0; 
        for(int i = 0; i< nums.length; i++)
        {
           ans += (long)Math.abs(nums[i]-val) * cost[i];
        }
        return ans;
    }
}