目录
- 一、前言
- 二、基于轨迹与路面重心偏离度误差的预测自动差速小车循迹控制策略
- 三、轨迹图像的处理要点
- 四、本篇部分核心控制策略python代码:
- 五、结论
一、前言
基于最近的测试,得到了一种粗略控制的算法,其控制效果适合单线路和急转弯的情况,本人认为可以稍微进行改进适用于十字路口等复杂轨迹的单目视觉循迹运行,本篇是对python机器人编程——差速机器人小车的控制,控制模型、轨迹跟踪,轨迹规划、自动泊车(中)未完成部分给补充,也提供了一种比较可靠和新的思路——我们把它暂且命名为《基于轨迹与路面重心偏离度误差的预测自动差速小车循迹控制》。

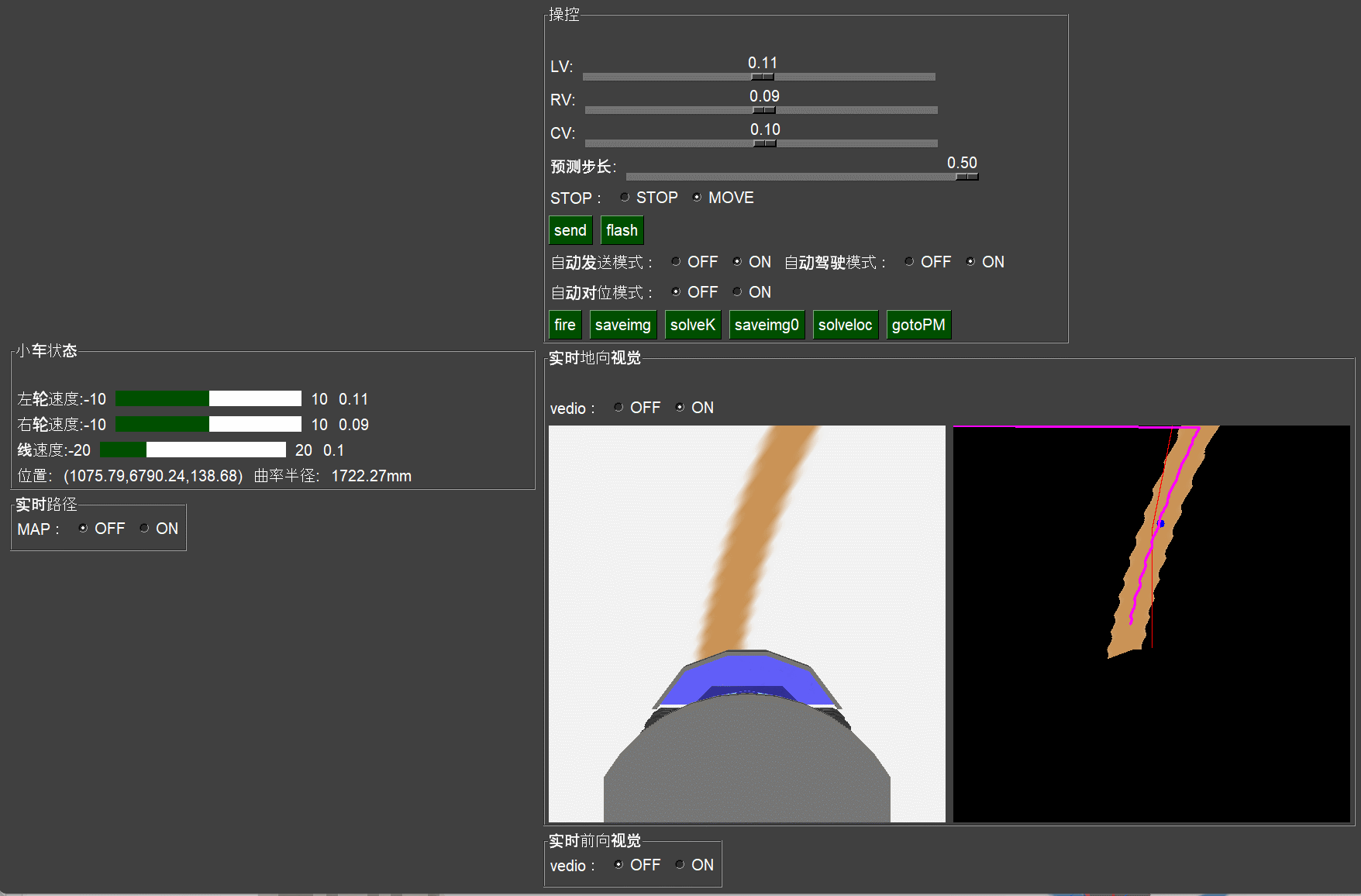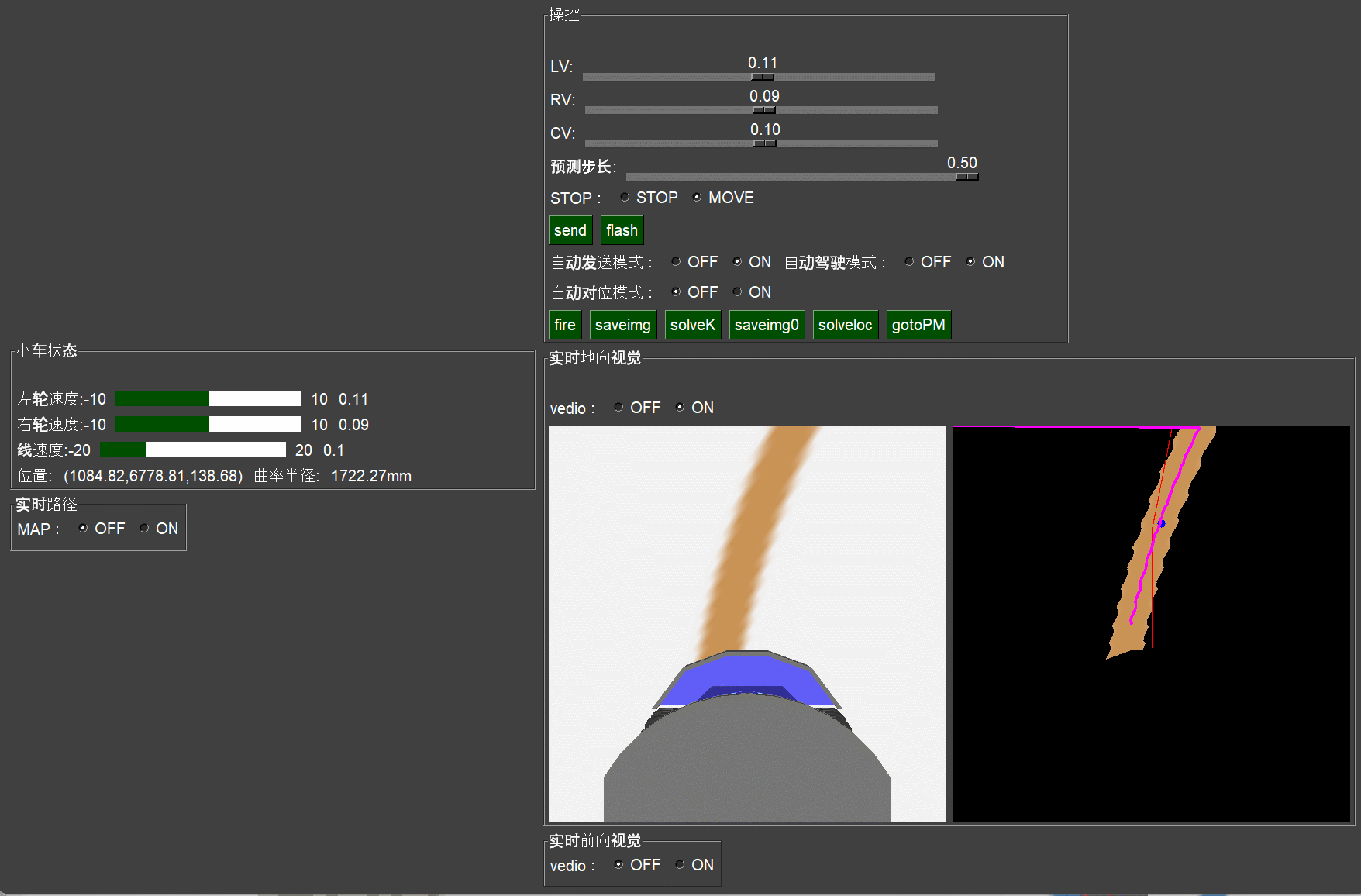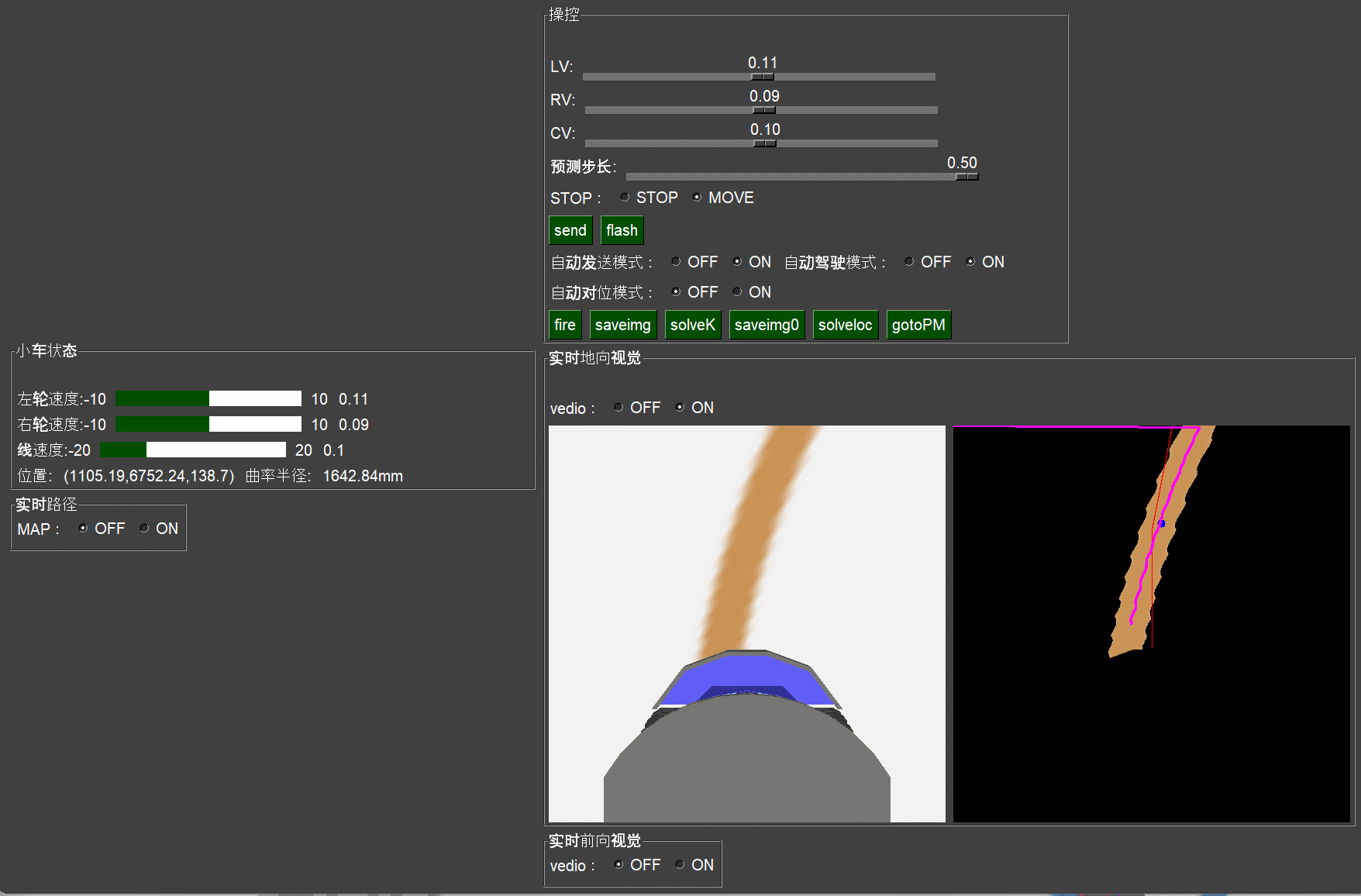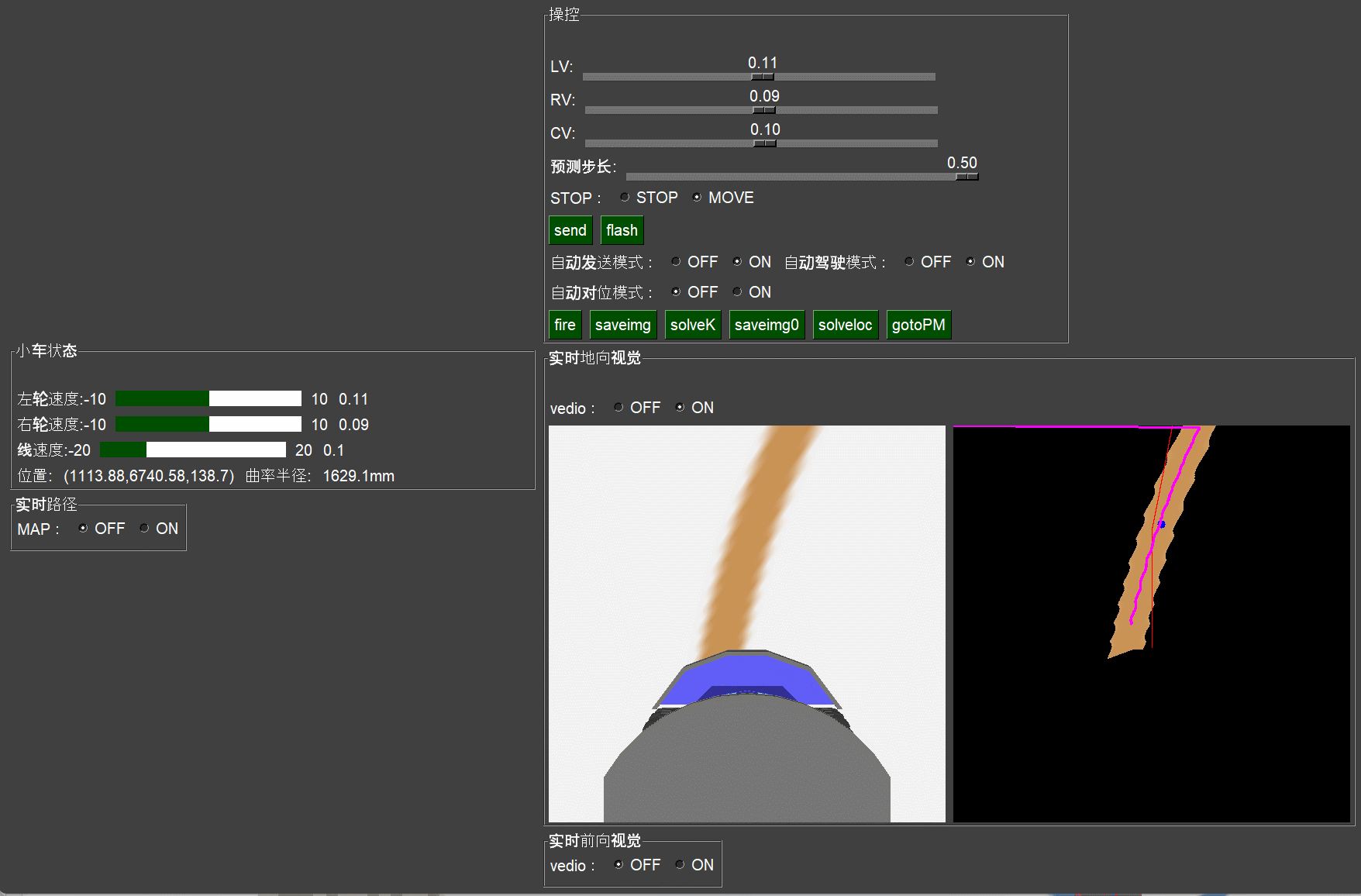
如上图所示,该算法可以在速度360m/h的情况下,比较粗略的自动转过一个大于90度的急转弯。虽然线不是非常贴切,但是我们认为这个方法实际比较可行。下面详细对该方法做个说明:
二、基于轨迹与路面重心偏离度误差的预测自动差速小车循迹控制策略
该方法中差速小车的控制还是用前面提到的预测控制方法,程序是一个以步长为dt的不断根据接受到的图像进行小车正反方向进行未来时刻轨迹预测的过程,并在边界条件下搜索出误差最靠近图像采集轨迹的小车左右轮子对应的速度即为当前步序的最优小车速度设定值。具体的算法流程伪代码如下:
- while True:
-
记录预测间隔累计时间con_Hz=con_Hz+1 -
读取摄像头图像,并进行处理(具体方法见第三节)获得路径的重心图像坐标cu、cv -
if 当时间间隔到达预测控制的步长时con_Hz=300毫秒: -
con_Hz=0 -
进入预测控制模块best_move(处理过的轨迹,当前的速度状态clv,重心坐标): -
定义最佳速度设定值bestv=clv -
定义预测的微增速度dv=0.001 -
定义预测的边界范围vmax=10 -
for i in vmax:#速度增加的方向预测vmax个dv -
左轮的速度sl_n=当前速度+i*dv -
根据恒定速度计算右轮速度 -
计算当前速度下未来2.5秒后(可以调整)的轨迹线存在pv、pu的list中 -
将当前预测轨迹按照摄像头内参转化到图像坐标 -
计算预测轨迹的重心图像坐标(cpu、cpv) -
计算重心距离dei=sqrt((cpu-cu)**2+(cpv-cv)**2) -
if dei<de: -
更新误差de=dei -
更新bestv=sl_n -
for i in vmax:#速度减小的方向预测vmax个dv -
左轮的速度sl_n=当前速度-i*dv -
根据恒定速度计算右轮速度 -
计算当前速度下未来2.5秒后(可以调整)的轨迹线存在pv、pu的list中 -
将当前预测轨迹按照摄像头内参转化到图像坐标 -
计算预测轨迹的重心图像坐标(cpu、cpv) -
计算重心距离dei=sqrt((cpu-cu)**2+(cpv-cv)**2) -
if dei<de: -
更新误差de=dei -
更新bestv=sl_n -
reurn bestv#返回最优控制速度设定值 -
将当前最优控制速度值下发至小车 -
进入下一个循环。
以上是主要的算法描述。
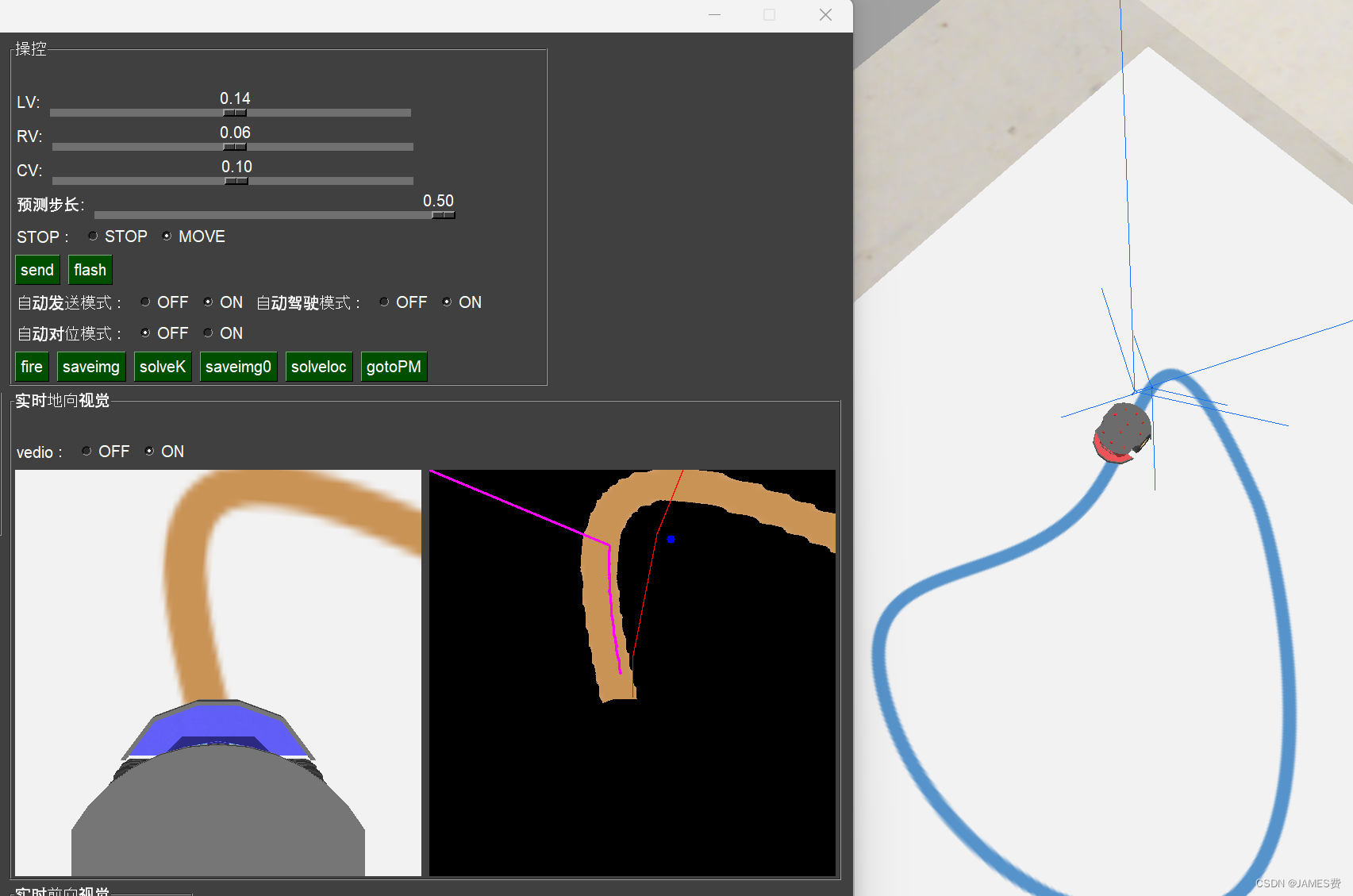
根据这个算法,在仿真环境下,跑了很久,也没有大的偏离出轨道。如上图所示,中间的黑色图中:黄色为处理过的路径,蓝色的点为路径的重心点位置,红色的线在当前边界下最佳速度设定值时的预测未来行驶轨迹,当前轨迹是最靠近蓝色重心的,小车始终在这样的策略下运行。
三、轨迹图像的处理要点
对于获取的轨迹图像处理,主要流程如下:
- 获取摄像头当前的图像img
- 根据颜色选择算法留下黄色轨迹部分信息图像bimg
- 将bimg图像进行二值化,留下轨迹的像素为1,得到图binary
- 去除binary中小车部分的像素(图像的小下半部分)得到一个新的binary
- 计算当前轨迹的重心点cu、cv,供输入预测控制模块
图像的重心计算代码示例如下:
import cv2
import numpy as np
import matplotlib.pyplot as plt
# Load the binary image
img = cv2.imread('binary_image.png', 0)
# Calculate the moments of the image
M = cv2.moments(img)
# Calculate the centroid
cx = int(M['m10'] / M['m00'])
cy = int(M['m01'] / M['m00'])
# Print the centroid coordinates
print(f'Centroid: ({cx}, {cy})')
# Draw a circle at the centroid
img_with_centroid = cv2.circle(img.copy(), (cx, cy), 5, (255, 0, 0), -1)
# Display the image with the centroid
plt.imshow(img_with_centroid, cmap='gray')
plt.show()
四、本篇部分核心控制策略python代码:
def best_move(sl,Pathimg,vc=0.1,dt=0.5,barycenter=(256,256)):
#控制增量
dvl=0.001
#要预测的控制量
sl_n=sl
#最优的控制量
best_sl=sl
mod="G"
#方差
de=500
dei=e+100
Gbest_sl=sl
for i in range(10):#逐次减小控制量
sl_n=sl_n-i*dvl
#待入预测函数获取预测序列
xx,yy,tt=predicate(0,0,math.pi/2,sl_n,step=5,dt=dt,vc=vc,dspeed=True)
#中心轨迹转化为车头轨迹
pv=[]
pu=[]
#将小车坐标转化到图像坐标
for i in range(len(xx)):
puv1=realxy2uv(xx[i],yy[i],Pathimg,xymax=0.5,zero="self_define",dzero=(256,286))
pu.append(puv1[0])
pv.append(puv1[1])
cpu=np.average(pu)
cpv=np.average(pv)
dei= np.sqrt((barycenter[0]-cpu)**2+(barycenter[1]-cpv)**2)
if dei<de:
de=dei
Gbest_sl=sl_n
sl_n=sl
for i in range(10):#逐次增大控制量
sl_n=sl_n+i*dvl
xx,yy,tt=predicate(0,0,math.pi/2,sl_n,step=5,dt=dt,vc=vc,dspeed=True)
#将小车坐标转化到图像坐标
pv=[]
pu=[]
for i in range(len(xx)):
puv1=realxy2uv(xx[i],yy[i],Pathimg,xymax=0.5,zero="self_define",dzero=(256,286))
pu.append(puv1[0])
pv.append(puv1[1])
cpu=np.average(pu)
cpv=np.average(pv)
dei= np.sqrt((barycenter[0]-cpu)**2+(barycenter[1]-cpv)**2)
if dei<de:
de=dei
Gbest_sl=sl_n
print("Gbest_sll:",best_sl)
#返回最优控制量
if mod=="G":
return Gbest_sl
else:
return best_sl,np
五、结论
后续还有对复杂轨迹的处理需要改进。如需要本篇的仿真环境和源代码,可以加入公众号或者私信留言。