| 一、实验目的: 理解动态规划算法的基本思想和设计步骤; 掌握动态规划算法的典型应用范例——矩阵连乘。 | ||||||||
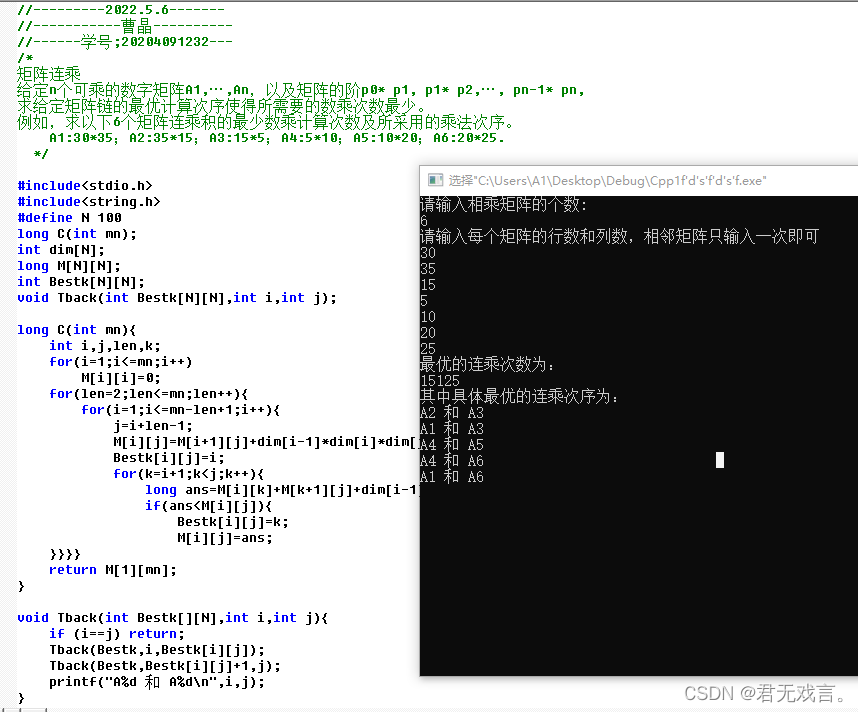
| 二、实验内容 矩阵连乘 给定n个可乘的数字矩阵A1,…,An,以及矩阵的阶p0* p1, p1* p2,…, pn-1* pn,求给定矩阵链的最优计算次序使得所需要的数乘次数最少。 例如,求以下6个矩阵连乘积的最少数乘计算次数及所采用的乘法次序。 A1:30*35;A2:35*15;A3:15*5;A4:5*10;A5:10*20;A6:20*25. 程序代码: #include<stdio.h> #include<string.h> #define N 100 long C(int mn); int dim[N]; long M[N][N]; int Bestk[N][N]; void Tback(int Bestk[N][N],int i,int j); long C(int mn){ int i,j,len,k; for(i=1;i<=mn;i++) M[i][i]=0; for(len=2;len<=mn;len++){ for(i=1;i<=mn-len+1;i++){ j=i+len-1; M[i][j]=M[i+1][j]+dim[i-1]*dim[i]*dim[j]; Bestk[i][j]=i; for(k=i+1;k<j;k++){ long ans=M[i][k]+M[k+1][j]+dim[i-1]*dim[k]*dim[j]; if(ans<M[i][j]){ Bestk[i][j]=k; M[i][j]=ans; }}}} return M[1][mn];} void Tback(int Bestk[][N],int i,int j){ if (i==j) return; Tback(Bestk,i,Bestk[i][j]); Tback(Bestk,Bestk[i][j]+1,j); printf("A%d 和 A%d\n",i,j); } void main() {
int i,mn; printf("请输入相乘矩阵的个数:\n"); scanf("%d",&mn); printf("请输入每个矩阵的行数和列数,相邻矩阵只输入一次即可\n"); while(EOF !=mn){ for(i=0;i<=mn;i++) scanf("%d",&dim[i]); printf("最优的连乘次数为:\n"); printf("%ld\n",C(mn)); printf("其中具体最优的连乘次序为:\n"); Tback(Bestk,1,mn); }} 程序测试及运行结果:
| ||||||||
| 分析与讨论:
我的思路是首先我们知道矩阵连乘的条件:第一个矩阵的列等于第二个矩阵的行,此时两个矩阵是可乘的,并且我们知道多个矩阵连乘的结果矩阵,其行列等于第一个矩阵的行和最后一个矩阵的列。所以先定义一个数组来保存它们的行和列数,以题目所给矩阵为例子。A1:30*35;A2:35*15;A3:15*5;A4:5*10;A5:10*20;A6:20*25.,那么定义一个数组为p={30,35,15,5,10,20,25}那么p[0],p[1]代表第一个矩阵的行数和列数,p[1],p[2]代表第二个矩阵的行数和列数…p[5],p[6]代表第六个矩阵的行数和列数。首先对数据进行初始化,然后通过不同的括号划分来对矩阵进行不同的连乘,通过自底向上的方法求得M(i,j)。
优点: 能够得到全局最优解;动态规划模型的缺点: 缺点:数值方法求解时存在维数灾并且没有统一的标准模型; 总结:当一个问题能够划分成n个相互独立的子问题的时候我们常用分治法来解决,但是当这些子问题不全相互独立的时候再用分治法就会多次重复计算子问题,造成资源的浪费,这个时候就用动态规划法,就是要划分出各种子问题,这些子问题的求法和原问题一模一样,我们可以直接利用求解好的子问题对原问题进行求最优 |
算法程序设计 之 矩阵连乘(3/8)
news2026/2/13 1:45:26
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/670194.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
JavaWeb之文件的上传和下载
文章目录 文件的上传基本介绍文件上传的HTTP协议的说明commons-fileupload.jar 常用API介绍说明fileupload类库的使用 文件的下载基本介绍和使用说明中文名乱码问题解决方案 文件的上传和下载,是非常常见的功能。很多的系统中,或者软件中都经常使用文件的…
使用spacy做分词的示例
下载数据:
aws s3 cp s3://applied-nlp-book/data/ data --recursive --no-sign-request
aws s3 cp s3://applied-nlp-book/models/ag_dataset/ models/ag_dataset --recursive --no-sign-request
上面第一份数据接近1GB,第二份接近3GB; 示…
买了一年CSDN年VIP,用着实在太爽
买一年CSDN的年VIP有多爽及使用攻略! 一、前言
这段时间,一旦打开CSDN就不断的弹出618活动,在电脑网上打开,一股白嫖之的气息吹来,让人直接忍不住剁手
最后经过近5天的挣扎,我还是受不了CSDN的蛊惑&#…
【工具分享】批量多目录图片如何转换PDF,一次性转换多级目录批量的PDF的转换,合并,输出另存等问题
在工作中我们经常要对图片进行批量转换PDF,由于文件量比较多,目录比较深,工作量比较大比较耗时费力,今天我们分享的主要解决以下问题:
1、单张图片的转换PDF:一张图临时转一下
2、多张图片转换成PDF&…
(二叉树) 1382. 将二叉搜索树变平衡 ——【Leetcode每日一题】
❓1382. 将二叉搜索树变平衡
难度:中等
给你一棵二叉搜索树,请你返回一棵 平衡后 的二叉搜索树,新生成的树应该与原来的树有着相同的节点值。如果有多种构造方法,请你返回任意一种。
如果一棵二叉搜索树中,每个节点…
whistle 使用介绍
什么是 whistle
来自 whistle 官网:http://wproxy.org/whistle/ 的介绍: whistle(读音[ˈwɪsəl],拼音[wēisǒu])基于Node实现的跨平台web调试代理工具,类似的工具有Windows平台上的Fiddler,主要用于查看、修改HTTP…
在 Python 中对日期和时间进行排序
文章目录 在 Python 中对日期和时间进行排序Python 中的日期时间模块sorted() 方法 使用 sorted() 方法对日期进行排序使用 sorted() 方法对时间进行排序使用 sorted() 方法对日期和时间进行排序总结 Python 是全世界程序员都在使用的一种高级解释型编程语言。 它最著名的是面向…
C++指针对象和异常(10)
异常(exception)
为什么有异常
异常在C用于错误处理,C语言中一般使用返回值表示错误,C对错误处理进行了扩展,统一使用异常机制来处理程序中发生的错误。
C的异常处理包括两个部分 ----- 抛出异常和捕获异常,如果抛出的异常被捕…
BW生成HANA视图权限配置
目录 1 操作步骤1.1 SAP HANA端1、创建用户2、常规信息3、配置角色4、配置系统权限5、配置对象权限 1.2 BW端1、SM30配置数据库连接参数2、SU01创建账户(与SAP HANA数据库账户名一致)3、使用RS2HANA_VIEW查看配置Assignment TypeDB Connection NameLimit…
如何解决亚马逊、ebay砍单、封号问题?稳定测评方案分析
很多卖家和工作室朋友询问我为什么在测评过程中经常遇到砍单和封号的问题。实际上,这并不难理解,因为测评所涉及的技术问题很多,并不能仅通过解决IP或环境的单一因素来实现稳定的测评。
目前市面上存在许多技术方案,例如指纹浏览…
火山引擎Dataleap治理实践:如何降低数仓建设成本
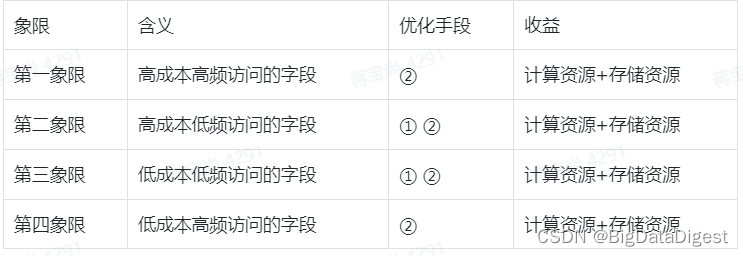
背景
存储与计算资源是数仓建设的基础,也是数仓建设中的重要成本支出。而随着数仓建设规模逐渐扩大、时间跨度逐渐拉长,将不可避免的出现数据表、任务、字段的冗余。为了减轻资源负担,降低数仓维护成本,需要对数仓建设成本进行治…
微信小程序-上传代码失败,提示分包大小超过限制
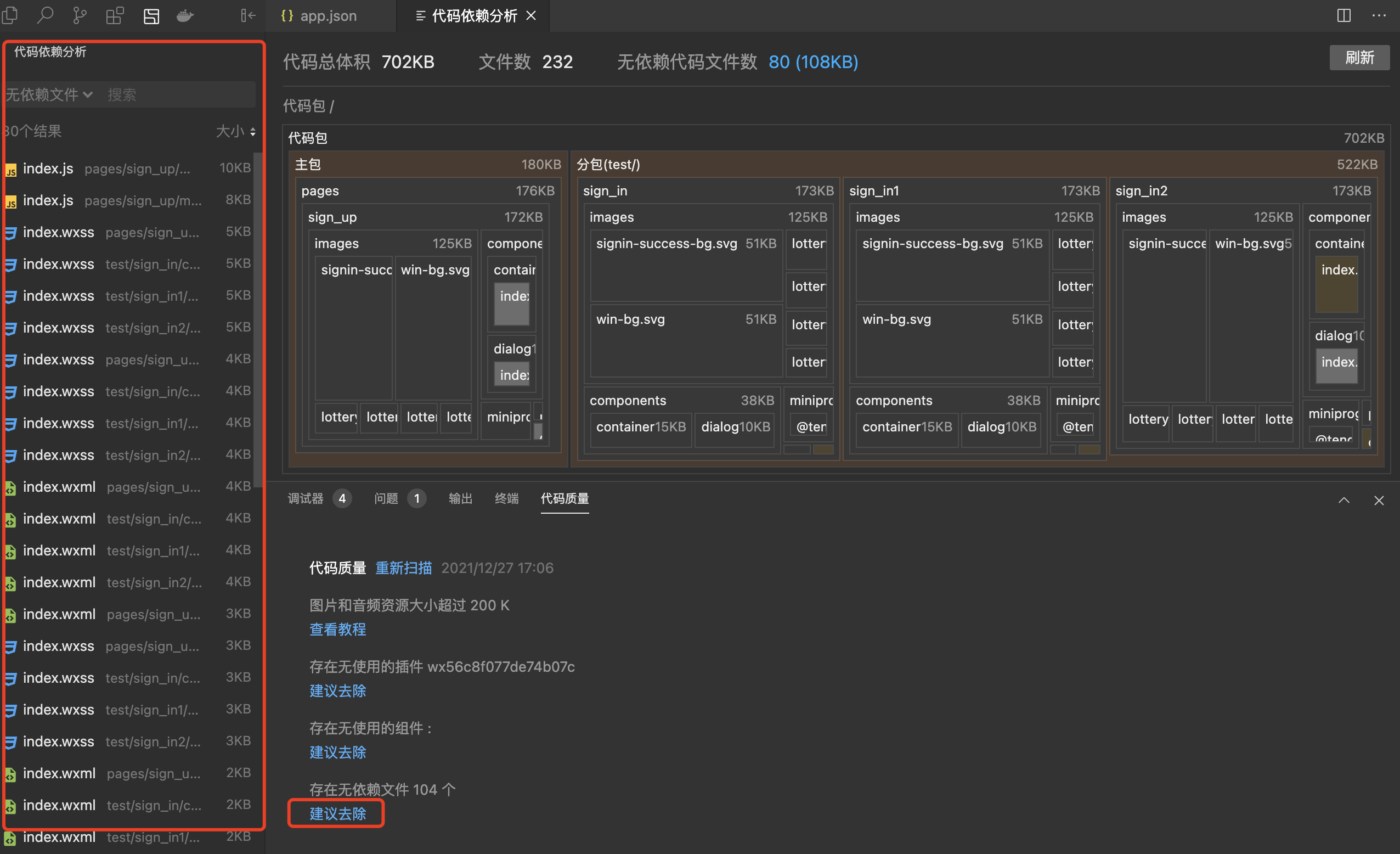
开发者可通过开发者工具中的性能扫描工具提前发现代码中的可优化项:
1. 代码包不包含插件大小超过 1.5 M
【建议】小程序代码包单个包大小限制为2M。因此我们建议开发者在开发时,如果遇到单包体积大于1.5M的情况,可以采取分包的方式&#x…
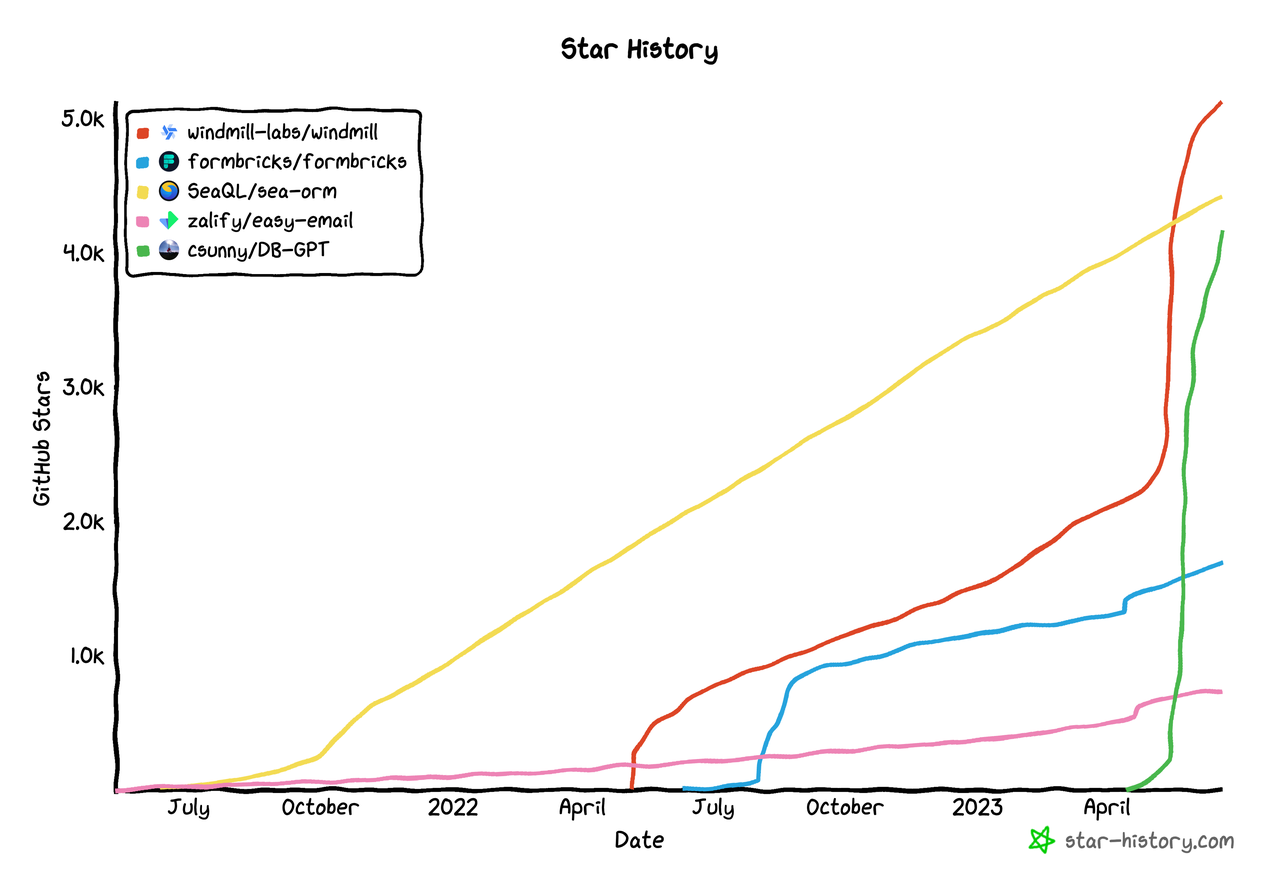
Star History 月度开源精选|2023 年 5 月
收集完五月的 Star History 精选之后我们惊讶地发现居然有那么多好玩好用的项目,无论是低代码,或是可以帮你少写代码,即便不是专业开发者也可以上手了!
Windmill
Windmill 可以看做是 Airplane 的开源替代品 / Temporal 的低代码…
安科瑞产品在泛在电力物联网的应用
安科瑞虞佳豪
泛在电力物联网是以通讯技术为基础发展而来的新型物联网体系,其构建的核心是满足电网能源系统的智能判断和自适应调节能力,这将提高能源的替代和利用能力。对于电力物联网来说,通讯技术是其核心的技术内容之一,也是…
直播平台中的美颜SDK技术探究
而在直播过程中,美颜技术的应用已经成为了不可或缺的一部分。美颜技术能够让主播在镜头前变得更加漂亮自信,也能够提高直播的观看体验。在直播平台中,美颜SDK技术的探究就显得尤为重要。
一、美颜SDK技术的定义
美颜SDK技术是一种通过算法…
Java中的增强 for 循环 foreach
foreach 是 Java 中的一种语法糖,几乎每一种语言都有一些这样的语法糖来方便程序员进行开发,编译期间以特定的字节码或特定的方式来对这些语法进行处理。能够提高性能,并减少代码出错的几率。在 Java 中还有比如 泛型、自动拆箱、自动装箱、内…
【集合数据类型详解】——基础语法
目录索引 集合特点:集合用处:去重操作: 创建集合:实例:实例2: 集合运算:交集:并集:补集:差集: 集合特点: 同一集合中,只能…
ssm酒店住宿预定系统-计算机毕设 附源码 87020
ssm酒店住宿预定系统 目 录 摘要 1 绪论 1.1 研究背景 1.2开发意义 1.3ssm框架 1.4论文结构与章节安排 2 2 酒店住宿预定系统系统分析 2.1 可行性分析 2.2 系统流程分析 2.2.1 数据增加流程 2.2.2 数据修改流程 2.2.3数据删除流程 2.3 系统功能分析 2.3.1功能性分…
使用Servlet完成单表的增删改查功能以及使用模板方法设计模式解决类爆炸问题(重写service模板方法)
使用Servlet做一个单表的CRUD操作
开发前的准备
导入sql脚本创建一张部门表
drop table if exists dept;
create table dept(deptno int primary key,dname varchar(255),loc varchar(255)
);
insert into dept(deptno, dname, loc) values(10, XiaoShouBu, BeiJing);
inser…
【读书笔记】《认知觉醒》- 周岭
不停的阅读,然后形成自己的知识体系。 2023.06.25 读 文章目录 自序 开启自我改变的原动力上篇 内观自己,摆脱焦虑第一章 大脑——一切问题的起源第一节 大脑:重新认识你自己三重大脑高低之分与权力之争成长就是克服天性的过程 自序 开启自我…